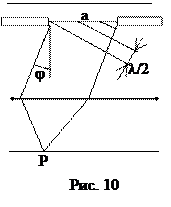Интерференция световых волн

 

Интерференцией называется явление перераспределения энергии в пространстве при наложении когерентных волн.

Когерентными называются волны одного направления, с одинаковыми плоскостями колебаний светового вектора, одинаковой частотой и с постоянной во времени разностью фаз.

Когерентные волны можно получить, разделяя одну световую волну на две с помощью отражения и преломления света.

Условия наблюдения максимумов и минимумов интерференции определяются разностью фаз складываемых колебаний.

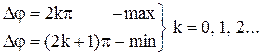(46)

Разность фаз интерферирующих волн связана с оптической разностью хода

 

D = l ₂ – l ₁,

 

где l – оптическая дина пути световой волны. При этом l = S×n, где S – геометрическая длина пути световой волны в однородной среде с показателем преломления n. Кроме того, при нахождении l надо учитывать, что при отражении от оптически более плотной среды световая волна меняет фазу на p. В этом случае к оптической длине пути надо прибавить (или отнять) l₀/2.

Связь разности фаз с оптической разностью хода дает общие условия наблюдения интерференционных максимумов и минимумов:

(47)

Рис. 6

 

Рассмотрим основные случаи интерференции

1. Интерференция наблюдается на экране, расположенном параллельно двум когерентным источникам в виде щелей (опыт Юнга, зеркала Френеля, бипризма Френеля) (Рис. 6).

L – расстояние от экрана до источников, отстоящих друг от друга на расстоянии d (d << L);

x – расстояние от центра интерференционной картины до k-ой интерференционной полосы.

 

 

Тогда (48)

 

2. Интерференция при отражении от тонких пленок. При падении света на тонкую пленку происходит отражение от обеих поверхностей пластинки. В результате возникают когерентные волны 1 и 2, которые могут интерферировать (рис. 7). При этом

 

, (49)

 

где d – толщина пленки, n – показатель преломления, a – угол падения, l₀/2 – добавочная разность хода, учитывающая смену фазы на p при отражении 1-й волны от более плотной среды (пленки).

 

 

Рис. 8

3. Кольца Ньютона – пример полос равной толщины, наблюдаемых при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластинки и плосковыпуклой линзы с большим радиусом кривизны (рис. 8).

 

Тогда радиусы темных колец Ньютона в отраженном свете 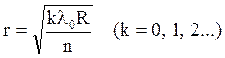, (50) а радиусы светлых колец Ньютона в отраженном свете

. (51)

 

Здесь R – радиус кривизны линзы, n – показатель преломления вещества между линзой и пластинкой.

 

1.4. Дифракция световых волн

 

Дифракцией называется огибание волной препятствий. Дифракция выражена достаточно сильно, если длина волны соизмерима с размерами препятствия. Возникновение дифракции можно объяснить с помощью принципа Гюйгенса: каждая точка, до которой доходит волновое движение, служит центром вторичных волн; огибающая этих волн дает положение фронта волны в следующий момент. Для количественной оценки результатов дифракции и нахождения амплитуды результирующей волны в любой точке пространства Френель дополнил принцип Гюйгенса представлением о когерентности вторичных волн и их интерференции.

Различают: 1) дифракцию плоской волны – дифракцию Фраунгофера и 2) дифракцию сферической волны – дифракцию Френеля

Расчеты с использованием принципа Гюйгенса – Френеля – чрезвычайно трудная задача. Поэтому для качественной оценки результатов дифракции Френель предложил разбивать фронт волны не на бесконечное множество точечных источников, а на конечное число зон. Зонами Френеля называются участки фронта волны, построенные таким образом, что расстояние от краев каждой зоны до точки наблюдения отличаются на l/2.

Рис. 9

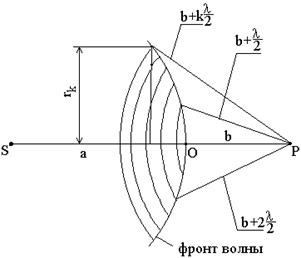Построение зон для сферической волны, испущенной источником S, показано на рис. 9. Колебания, приходящие в точку наблюдения P от аналогичных точек двух соседних зон, будут находиться в противофазе. Поэтому и результирующие колебания, создаваемые каждой из зон в целом, будут для соседних зон отличаться по фазе на p.

Радиус внешней границы k-ой зоны Френеля в этом случае

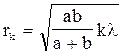, (52)

где а – расстояние от источника света до фронта волны, b – расстояние от точки наблюдения до вершины фронта волны О.

Для плоской волны радиус находится как

 

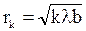. (53)

 

Для качественной оценки результата дифракции на малом круглом отверстии достаточно найти количество зон Френеля, попавших в это отверстие. Если количество зон четное, то в точке Р будет минимум, если нечетное – максимум.

Аналогично оценивается дифракция Фраунгофера на узкой щели (рис. 10).

Открытая часть фронта волны, дошедшей до щели, разбивается на параллельные краям щели зоны Френеля шириной , где j – угол дифракции. Таких зон на ширине щели укладывается . Если N четное, то в точке Р – минимум, если N нечетное, то в точке P – максимум. Тогда

 

(54)

 

d

a

Большое практическое значение имеет дифракция Фраунгофера на так называемой дифракционной решетке. Дифракционной решеткой называется совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние, щелей (рис. 11).

Рис.11

Расстояние d между серединами соседних щелей называется постоянной или периодом решетки. При этом в направлениях, для которых разность хода волн от соседних щелей равна целому числу длин волн, будут наблюдаться максимумы интенсивности, называемые главными. Таким образом, условие главных максимумов имеет вид

 

dsinj = 2kl/2, k = 0, 1, 2... (55)

 

При этом интенсивность главных максимумов I_max пропорциональна интенсивности I_j, создаваемой в направлении j одной щелью. I_max = N²I, (56),

где N – общее число щелей решетки.

Дифракционная решетка служит спектральным прибором, разрешающая способность которого (57)

где Dl – наименьшая разность длин волн двух близких спектральных линий с длинами волн l и l+Dl, при которых они еще воспринимаются раздельно (разрешаются).

Разрешающая способность дифракционной решетки может быть найдена по формуле

R = kN, (58)

 

где k – порядок дифракционного спектра, N – общее число щелей решетки.

 

1.5. Поляризация световых волн

 

В естественном свете колебания различных направлений быстро и беспорядочно сменяют друг друга. Свет, в котором направления колебаний упорядочены каким-либо образом, называют поляризованным. Обычно ограничиваются рассмотрением плоскополяризованного света, то есть такого, в котором колебания светового вектора происходят только в одной плоскости.

Плоскополяризованный свет получают из естественного с помощью приборов – поляризаторов. Эти приборы пропускают только колебания, параллельные плоскости, называемой плоскостью поляризатора. Если через поляризатор пропустить естественный свет с интенсивностью I_ест, то интенсивность прошедшего поляризованного света

 

Рис.12

I = 0,5I_ест. (59)

Если на поляризатор падает уже плоскополяризованный свет с амплитудой А₀ и интенсивностью I₀ (рис. 12), то сквозь прибор пройдет составляющая колебания с амплитудой А = А₀ cos j, где j – угол между плоскостью колебаний падающего света и плоскостью поляризатора. Следовательно, интенсивность прошедшего света I определяется выражением

 

I = I₀ cos²j (60)

 

Соотношение (60) носит название закона Малюса.

Действие поляризаторов разных типов основано либо на явлении поляризации света при отражении его от диэлектрика, либо на поляризации при двойном лучепреломлении, которое наблюдается при прохождении света через анизотропные вещества (кристаллы).

Рис.13

В первом случае имеет место закон Брюстера, который гласит, что отраженный от диэлектрика свет будет полностью поляризован, если тангенс угла падения a_Б равен относительному показателю преломления сред n₂₁ = n₂/n₁ (рис. 13):

 

tga_Б = n₂₁. (61)

 

ТЕМА № 2

 

КВАНТОВАЯ ФИЗИКА

КВАНТОВАЯ ОПТИКА

Тепловое излучение

 

Тепловым излучением называется испускание электромагнитных волн за счет внутренней энергии тел. Оно имеет место при любой температуре. Приведем величины, характеризующие этот вид излучения:

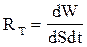– энергетическая светимость – величина, равная энергии, испускаемой единицей поверхности тела в единицу времени по всем направлениям. Она является функцией температуры.

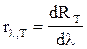– спектральная плотность энергетической светимости – величина, равная энергии, испускаемой единицей поверхности тела в единицу времени по всем направлениям в единичном интервале длин волн. Это функция длины волны и температуры.

– поглощательная способность – безразмерная величина, равная отношению потока энергии, поглощенной телом, к потоку энергии, падающей на тело при данной температуре и длине волны.

Тело, полностью поглощающее упавшее на него излучение всех длин волн, называется абсолютно черным (a_l,T º 1).

 

Закон Кирхгофа. Отношение спектральной плотности энергетической светимости к поглощательной способности не зависит от природы тела, оно является для всех тел одной и той же универсальной функцией длины волны и температуры:

. (1)

Экспериментально найденная с помощью изучения излучения абсолютно черного тела функция Кирхгофа имеет вид, приведенный на рис. 1.

Теоретически вид функции Кирхгофа нашел Планк, предположивший, что излучение испускается излучающими телами не непрерывно, а определенными порциями – квантами. Энергия каждого кванта:

 

, (2)

Рис. 1

где – постоянная Планка, Дж×с

w – круговая частота колебаний в электромагнитной волне.

Формула Планка имеет вид

 

(3)

 

Как следует из закона Кирхгофа, f(l,T) º r_l,T для абсолютно черного тела.

 

Закон Стефана – Больцмана. Энергетическая светимость абсолютно черного тела прямо пропорциональна четвертой степени его абсолютной температуры.

 

R_T = sT⁴, (4)

где s – постоянная Стефана – Больцмана:

 

Закон смещения Вина. Длина волны, на которую приходится максимум спектральной плотности энергетической светимости абсолютно черного тела, обратно пропорциональна его абсолютной температуре. (рис. 1):

 

l_max = b/T, (5)

 

где b – постоянная Вина, b = 2,9×10^-3 м×К.

 

Фотоны

 

Световые кванты, то есть частицы, в виде которых распространяется свет, получили название фотонов. Они обладают энергией (формула (2), массой

 

, (6)

и импульсом или , (7)

где – волновой вектор – вектор, модуль которого равен волновому числу, а направление совпадает с направлением фазовой скорости световой волны.

Взаимодействием фотонов с веществом объясняется ряд явлений и эффектов.

Фотоэффект

 

Внешним фотоэффектом называется испускание электронов с поверхности металлов под действием света. Фотоэффект объясняется взаимодействием фотонов со свободными электронами металлов.

Уравнение Эйнштейна для фотоэффекта:

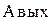= + , (8)

где А_вых – работа выхода электрона из металла (табличная величина);

– максимальная кинетическая энергия электрона.

Из уравнения (8) следует, что фотоэффект возможен только при условии

A_вых , или

, (9)

где w₀ называется красной границей фотоэффекта.

Для торможения вылетающих электронов необходимо приложить задерживающее напряжение U_з , которое можно найти из условия

mu_m²/2 = eU₃, (10)

где e – заряд электрона.

Давление света

 

Тот факт, что свет оказывает давление на поверхность, на которую он падает, просто объясняется передачей фотонами этой поверхности некоторого импульса. Тогда формула для светового давления имеет вид

 

P = w(1+r), (11)

 

где w – объемная плотность энергии излучения, падающего на тело, r – коэффициент отражения. w можно представить как w = I/c. Здесь I – интенсивность падающего света (плотность потока энергии излучения), с – скорость света.