Отметим, что для обоснования частичного выбора ведущего элемента в качестве примера был приведен крайний случай, когда на месте ведущего элемента после очередного исключения образуется ноль. Между тем польза от этого уточнения метода проявляется и не в таком крайнем, но гораздо более часто встречающемся случае, когда ведущий элемент мал по абсолютной величине. Вспомним, что компьютер, как, впрочем, и человек, при вычислениях запоминает лишь какое-то определенное количество цифр числа. Теперь попробуем решить такую систему:
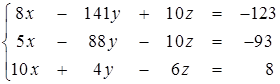(2.13)
Нетрудно, кстати, убедиться, что решением этой системы будут значения
. (2.14)
Вычисления будем производить приближенно, округляя результаты вычислений до трех значащих цифр.
Сначала решаем систему, не применяя выбора ведущего элемента. Поскольку 
и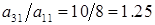 
, после исключения первой неизвестной x система принимает такой вид:
(2.15)
Выпишем отдельно вычисления:
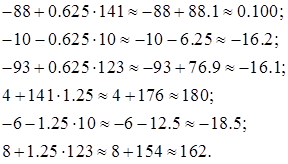(2.16)
Таким образом, после исключения x имеем
(2.17)
Теперь исключаем y из третьего уравнения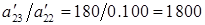 
, и третье уравнение принимает вид
(2.18)
или после вычислений
. (2.19)
Вычисляя теперь неизвестные, получаем:
(2.20)
Полученное решение не имеет ничего общего с тем, что должно получиться (2.14)!
Что ж, давайте, вернемся к тому моменту решения, когда нам следовало бы применить процедуру выбора ведущего элемента (2.17). Итак, поскольку коэффициент при y в третьем уравнении больше, чем во втором, переписываем (2.17) таким образом:
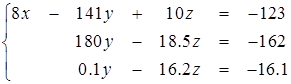(2.21)
Исключаем y из последнего уравнения. Теперь 
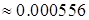и третье уравнение (2.21) приводится к
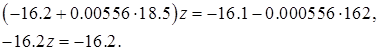
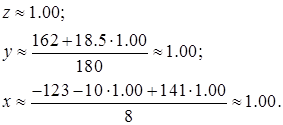(2.22)
Что за чудеса? Всего то и сделали, что две строчки местами поменяли, а вместо абракадабры (2.20) получили точное решение (2.22).
Никакой мистики в этом, конечно, нет. Чтобы понять причину этого явления, вернемся к первой строке вычислений (2.16), в которой было получено значение ведущего элемента при y, равное 0.100. Если отказаться от округлений и попытаться вычислить точное значение ведущего элемента, мы получим:
. (2.23)
Ошибка округления составила 25%. А ведь этот ведущий элемент используется в дальнейших вычислениях и портит нам все результаты. Причина такого катастрофического падения точности типична для приближенных вычислений:
При вычитании близких по модулю чисел (у нас 88.0 и 88.1) старшие цифры взаимно уничтожаются и, соответственно, уменьшается количество верных цифр в результате.
В нашем случае после взаимного уничтожения двух восьмерок ответ содержит лишь одну верную значащую цифру.
Когда вычисления производит компьютер, в памяти сохраняется больше цифр – 6-7 при обычной точности и 17-18 при двойной точности. Однако и количество уравнений в системах обычно гораздо больше, чем в нашем примере. Поэтому хорошая программа «понимает», что малая величина ведущего элемента говорит, скорее всего, о том, что в этом значении мало верных цифр, и лучше попробовать в этой роли другого кандидата.
Замечание. Не следует забывать и о том, что некоторые системы вообще не имеют решения. Например,
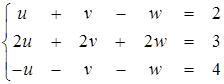(2.24)
после первого же шага исключения дает нам
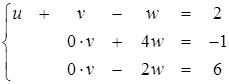(2.25)
Очевидно, что система (2.25) решений иметь не может. С другой стороны, и алгоритм Гаусса на (2.25) застопорится – оба кандидата на роль ведущего элемента равны нулю.
Подведем итог:
1. При практическом применении метода Гаусса необходимо осуществлять выбор ведущего элемента после каждого шага исключения.
2. Величина ведущего элемента не должна быть меньше некоторого предельного значения. Малое значение ведущего элемента может получиться по двум причинам: а) в результате вычитания двух близких по модулю чисел значение имеет мало правильных цифр и ему нельзя верить; б) на самом деле система вообще не имеет решения, а малое число получено вместо нуля из-за ошибок округления. Обе причины хуже некуда – результатам расчетов верить нельзя.
[1] Гаусс Карл Фридрих (1777-1855) – немецкий ученый. Труды Гаусса оказали большое влияние на развитие алгебры, теории чисел, дифференциальной геометрии, математической физики, теории электричества и магнетизма, геодезии и астрономии
