Если матрица 
содержит в своих столбцах 
нормированных собственных векторов симметричной матрицы 
, то
Доказательство этого утверждения сводится к последовательному выполнению двух матричных умножений. Вычисляя произведение 
, учитываем, что произведение матриц есть матрица, столбцы которой представляют собой произведение матрицы – первого сомножителя на соответствующие столбцы второго сомножителя. Следовательно,
.
Выполняя второе умножение, получим:
,
чтобы убедиться в правильности конечного результата, достаточно вспомнить, что:
1) произведение двух матриц есть матрица,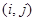 
-й элемент которой есть произведение 
-й строки первой матрицы-сомножителя на 
-й столбец второй матрицы-сомножителя;
2) столбцы матрицы ортонормированны, т.е.
.
Верно, кстати, и обратное утверждение: если 
– ортогональная матрица, приводящая матрицу к диагональному виду: 
, то столбцы – собственные вектора матрицы , а элементы диагональной матрицы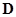 
– ее собственные значения.
Можно убедиться на подробно рассмотренном в § 5 примере, что если занести в матрицу собственные вектора:
(12.1)
и вычислить матричное произведение
(12.2)
то в результате действительно получится диагональная матрица с собственными значениями матрицы 
.
На этом факте линейной алгебры и основан итерационный метод решения задачи собственных значений, известный как метод Якоби. Метод этот заключается в следующем:
а) пусть дана симметричная матрица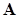 
;
б) предположим, что мы можем определить такую ортогональную матрицу 
, которая в результате преобразования
(12.3)
приводит к матрице 
, которая в каком-то смысле ближе к диагональной, чем 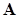. Смысл слов «ближе к диагональной» пока не уточняем. Заметим, что матрица 
подобна 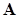и, следовательно, имеет те же собственные значения;
Подобные матрицы. Матрицы 
и 
подобны, если 
, где 
– невырожденная матрица.
Подобные матрицы имеют одинаковые собственные значения. В самом деле, пусть 
– собственное значение и 
– соответствующий собственный вектор матрицы , т.е. 
. Введем вектор 
или 
, что то же самое. Тогда
,
т.е., если является собственным значением матрицы , то оно является собственным значением матрицы 
.
в) для полученной матрицы 
аналогичным образом находим ортогональную матрицу 
и выполняем преобразование
; (12.4)
г) эти преобразования повторяем до тех пор, пока после какого-то 
-го преобразования не получим диагональную матрицу (точнее очень близкую к диагональной)
. (12.5)
Отметим, что, суммируя эти шаги, можно записать
, (12.6)
где
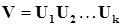(12.7)
является ортогональной матрицей как произведение ортогональных матриц.
В результате этой серии преобразований, как отмечалось ранее, мы должны получить на диагонали матрицы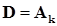 
собственные значения матрицы 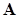и собственные вектора в столбцах матрицы 
;
д) остается решить один, но существенный вопрос: как получать матрицы 
, чтобы они обеспечивали сходимость процесса. В 1846 г. немецкий математик Карл Якоби доказал, что сходимость обеспечивается при следующем методе выбора матриц:
1) из всех внедиагональных элементов матрицы 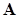выбирается наибольший по модулю – 
;
2) строится ортогональная матрица 
, которая отличается от единичной только элементами, стоящими на пересечении 
-х и -х строк и столбцов:
. (12.8)
Угол 
определяется таким образом
, (12.9)
чтобы после преобразования элемент 
, то есть 
-й элемент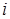 
-й строки, оказался равным нулю.
Пример.
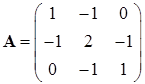
Характеристическое уравнение этой матрицы представляет собой уравнение третьей степени. Таким образом, для собственных значений и собственных векторов нетрудно получить аналитическим путем точные значения:
Теперь выполним несколько итераций Якоби и сравним полученный результат с точным решением:
Как видим, матрица 
неуклонно приближается к диагональной, с собственными значениями исходной матрицы 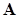на диагонали. Если мы попробуем согласно (12.7) определить собственные вектора
,
то увидим, что и они близки к аналитическому решению.
Литература
11.1. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1978. – 304с.
