Так же, как и прямой степенной, обратный степенной метод может оказаться медленно сходящимся. Напомним (см формулу (11.2)), что вектор  , принятый как начальный, можно представить как линейную комбинацию собственных векторов исследуемой матрицы
, принятый как начальный, можно представить как линейную комбинацию собственных векторов исследуемой матрицы 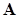 :
:
 . (11.13)
. (11.13)
Тогда после  -го шага обратного степенного метода
-го шага обратного степенного метода
 . (11.14)
. (11.14)
Ясно, что вектор  тем скорее станет доминирующим, чем больше будет отношение
тем скорее станет доминирующим, чем больше будет отношение  . Быстрее всего последовательность (11.14) сходилась бы, если бы
. Быстрее всего последовательность (11.14) сходилась бы, если бы 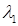 было очень малой величиной, близкой к нулю. К сожалению,
было очень малой величиной, близкой к нулю. К сожалению, 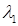 мы поменять не можем – ведь это и есть та величина, которую надо определить.
мы поменять не можем – ведь это и есть та величина, которую надо определить.
Вспомним, однако, свойство операции сдвига матриц:
Операцией сдвига по отношению к матрице называется вычитание из всех ее диагональных элементов одного и того же числа. Так, выражение

означает, что матрица  получена в результате сдвига матрицы
получена в результате сдвига матрицы  на
на  .
.
Для приложений очень важно следующее свойство этой операции: в результате операции сдвига собственные значения матрицы изменяются на величину сдвига, а соответствующие собственные вектора остаются прежними. В самом деле, пусть  собственное значение матрицы
собственное значение матрицы  , а
, а  – соответствующий собственный вектор. Тогда
– соответствующий собственный вектор. Тогда
 .
.
Если  – собственные значения матрицы
– собственные значения матрицы 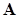 и
и  – соответствующие собственные векторы, то матрица
– соответствующие собственные векторы, то матрица  имеет собственные значения
имеет собственные значения  и собственные векторы
и собственные векторы  .
.
Согласно этому свойству, если нам будет известно достаточно хорошее приближение 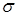 , то обратный степенной метод для матрицы
, то обратный степенной метод для матрицы 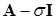 будет сходиться значительно быстрее, чем для матрицы
будет сходиться значительно быстрее, чем для матрицы 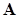 . Полученные для
. Полученные для 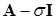 минимальное собственное значение (обозначим его
минимальное собственное значение (обозначим его  ) и собственный вектор
) и собственный вектор  позволяют определить минимальное собственное значение
позволяют определить минимальное собственное значение  и собственный вектор
и собственный вектор  матрицы
матрицы 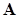 .
.
Остается вопрос, откуда взять хорошее приближение для 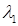 ? Практика и теоретические исследования показали, что лучшим выбором является отношение Рэлея:
? Практика и теоретические исследования показали, что лучшим выбором является отношение Рэлея:
 , (11.15)
, (11.15)
где, вообще говоря,  – произвольный вектор; мы же будем брать в качестве
– произвольный вектор; мы же будем брать в качестве  вектор, полученный в результате очередной итерации.
вектор, полученный в результате очередной итерации.
Более подробно это отношение и его свойства будут рассмотрены в следующих лекциях. Здесь же отметим еще, что для произвольного вектора 
 , (11.16)
, (11.16)
причем равенство достигается в случае, если  является первым собственным вектором матрицы
является первым собственным вектором матрицы 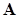 .
.
Пример. Вновь рассмотрим ту же матрицу

с тем же начальным вектором
 .
.
Кстати, поясним несколько странный выбор начального вектора в трех примерах этого параграфа. Обычно при применении степенных методов, не мудрствуя лукаво, в качестве начального вектора берут вектор с единичными элементами, т.е. следовало бы принять  . Однако в этом случае
. Однако в этом случае  точно совпало бы с собственным вектором матрицы
точно совпало бы с собственным вектором матрицы 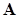 . Поэтому для того, чтобы показать, как в процессе итераций от исходного неточного вектора происходит постепенное приближение к собственному, пришлось немного «испортить» начальный вектор.
. Поэтому для того, чтобы показать, как в процессе итераций от исходного неточного вектора происходит постепенное приближение к собственному, пришлось немного «испортить» начальный вектор.
1-я итерация:
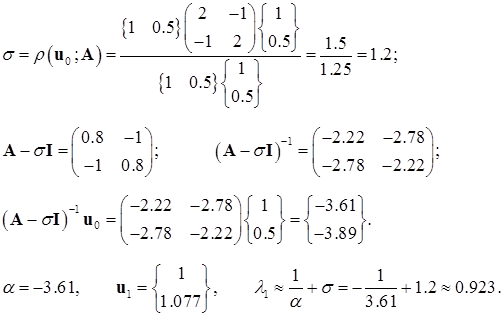
Как видим, уже первая итерация дала такую точность, какую методы без сдвига достигали лишь после третьей итерации. Для убедительности примера все-таки проведем еще одну итерацию.
2-я итерация:

Метод Якоби
Вспомним, что если  – ортогональная матрица, приводящая матрицу
– ортогональная матрица, приводящая матрицу  к диагональному виду:
к диагональному виду:  , то столбцы
, то столбцы  – собственные вектора матрицы
– собственные вектора матрицы  , а элементы диагональной матрицы
, а элементы диагональной матрицы 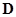 – ее собственные значения.
– ее собственные значения.
Ортогональные матрицы
Определение. Матрица

называется ортогональной, если ее столбцы ортонормированны, то есть
 .
.
Следствие. Для ортогональной матрицы ее обратная матрица равна ее транспонированной, т.е.  или, что то же самое,
или, что то же самое,  .
.
Еще одно следствие. Произведение ортогональных матриц есть ортогональная матрица. В самом деле, если 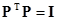 и
и  , то
, то
 .
.






