Дифференциальное уравнение теплопроводности в случае постоянных физических параметров тела имеет следующий вид:
 . (4.47)
. (4.47)
где  – температура тела, отсчитанная от температуры среды, окружающей
– температура тела, отсчитанная от температуры среды, окружающей
твердое тело, как от нуля;
 – время;
– время;
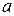 –коэффициент температуропроводности, постоянный во всем теле;
–коэффициент температуропроводности, постоянный во всем теле;
 – оператор Лапласа;
– оператор Лапласа;
 – координаты.
– координаты.
Приведенное уравнение (4.47) описывает бесконечное множество рассматриваемых тепловых процессов. Чтобы из целого класса явлений выделить единичное явление, необходимо к уравнению (4.47) присоединить начальные и граничные условия, а также задать значение коэффициента температуропроводности  .
.
Начальное условие должно представлять собой распределение температур во всей исследуемой области для момента времени  и может быть записано в виде
и может быть записано в виде
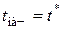 , (4.48)
, (4.48)
где  – известная температура в фиксированной точке тела с координатами
– известная температура в фиксированной точке тела с координатами
 ,
,  ,
,  в начальный момент времени.
в начальный момент времени.
Граничные условия могут быть заданы в виде равенства тепловых потоков на поверхности тела.
 , (4.49)
, (4.49)
где  – коэффициент теплопроводности, постоянный во всем теле;
– коэффициент теплопроводности, постоянный во всем теле;
 – коэффициент теплоотдачи;
– коэффициент теплоотдачи;
 – внешняя нормаль к поверхности тела.
– внешняя нормаль к поверхности тела.
Коэффициент теплоотдачи  в общем случае зависит от координат поверхности и времени. Поэтому, выражение для коэффициента теплоотдачи может быть записано в следующем виде:
в общем случае зависит от координат поверхности и времени. Поэтому, выражение для коэффициента теплоотдачи может быть записано в следующем виде:
 , (4.50)
, (4.50)
где 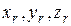 – координаты границы (поверхности) твердого тела.
– координаты границы (поверхности) твердого тела.
Для установления подобия процессов в рассматриваемом случае необходимо дифференциальные уравнения, начальные и краевые условия привести к безразмерному виду и обеспечить равенство безразмерных параметров, начальных и краевых условий. С этой целью введем следующие масштабные преобразования:
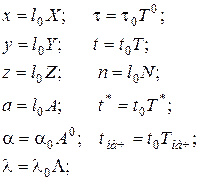 (4.51)
(4.51)
где величины, отмеченные индексом «нуль», являются размерными масштабами, выбор которых вначале произволен.
После введения преобразований (4.51) в уравнения (4.47), (4.48), (4.49) и (4.50) получаем
 (4.52)
(4.52)
при  и
и  . (4.53)
. (4.53)
На поверхности тела
 , (4.54)
, (4.54)
причем
 . (4.55)
. (4.55)
Чтобы уравнения (4.52) и (4.54) стали безразмерными, необходимо принять
 и
и  (4.56)
(4.56)
Система уравнений связи между масштабами (4.56) состоит из двух уравнений, содержащих пять масштабов. Поэтому три из них, имеющие независимые размерности, могут быть выбраны произвольно. Уравнения связи не содержат вовсе масштаба температур t 0, а поэтому он должен быть выбран произвольно.
Таким образом, выбирая произвольно следующие четыре масштаба с независимыми размерностями  , полагаем
, полагаем
 (4.57)
(4.57)
Равенство  следует понимать в том смысле, что в качестве масштаба длин можно выбирать любой геометрический параметр твердого тела.
следует понимать в том смысле, что в качестве масштаба длин можно выбирать любой геометрический параметр твердого тела.
Масштабы 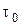 и
и  определяют с помощью уравнений (4.56) и равенства (4.57):
определяют с помощью уравнений (4.56) и равенства (4.57):
 (4.58)
(4.58)
Тогда выражения для безразмерных величин будут

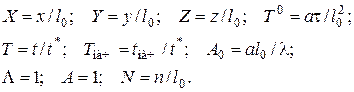 (4.59)
(4.59)
Дифференциальное уравнение (4.47), начальное (4.48) и граничное (4.49) условия теперь могут быть переписаны в безразмерном виде:
 (4.60)
(4.60)
 при
при  (4.61)
(4.61)
 (4.62)
(4.62)
Причем  (4.63)
(4.63)
Интеграл уравнения (4.63), удовлетворяющий начальному и граничному условиям (4.61) и (4.62) должен являться выражением, в котором зависимая переменная  представлена как функция всех величин (координат, времени и параметров), входящих в дифференциальные уравнения, начальные и граничные условия:
представлена как функция всех величин (координат, времени и параметров), входящих в дифференциальные уравнения, начальные и граничные условия:
 (4.64)
(4.64)
причем  и
и  определяются условиями (4.61) и (4.63).
определяются условиями (4.61) и (4.63).
Поэтому для обеспечения подобия необходимо и достаточно, чтобы в модели все критерии, входящие в интеграл исходного дифференциального уравнения (4.64) (кроме критериев 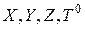 ), были равны соответствующим критериям образца.
), были равны соответствующим критериям образца.
Следовательно, задача осуществления подобия сводится к реализации следующих требований:
– обеспечения геометрического подобия модели и образца;
– тождественности в модели и образце безразмерных начального и граничного условий, т.е.:
 или
или  ;
; 

 или
или 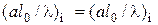 . (4.65)
. (4.65)
Если эти требования выполнены, то в сходственные моменты времени, т.е. при
 или
или  ,
,
и во всех сходственных точках, т.е. при
 или
или  ;
;
 или
или  ;
;
 или
или 
будет иметь место равенство
 или
или  ,
,
т.е. будет иметь место подобие температурных полей модели и образца.
Большой практический интерес представляют задачи теплопроводности в случае, когда физические параметры зависят от температуры.
Дифференциальное уравнение, описывающее такие явления, имеют вид
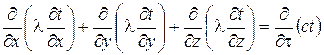 , (4.66)
, (4.66)
где  – коэффициент теплопроводности;
– коэффициент теплопроводности;
 – объемная теплоемкость, причем при
– объемная теплоемкость, причем при 
Начальное и граничное условия по-прежнему выражаются уравнениями (4.48) и (4.49), причем величина а как и ранее, определяется уравнением (4.50).
На основании рассуждений, аналогичных приведенным в предыдущей задаче, можно доказать, что после приведения уравнения (4.56) начального (4.48) и граничного (4.49) условий с помощью масштабных преобразований, подобных (4.52), получим два уравнения связи:
 , (4.67)
, (4.67)
включающее пять масштабов. Поэтому три из них, обладающие независимыми размерностями, могут быть выбраны произвольно. Кроме того, так же как и ранее, произвольно надлежит выбрать масштаб температуры. Таким образом принимаем:
 . (4.68)
. (4.68)
Остальные масштабы определяем из уравнений связи (4.67) и равенств (4.68):
 . (4.69)
. (4.69)
где 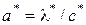 – коэффициент температуропроводности.
– коэффициент температуропроводности.
После этого можно выписать выражения для безразмерных величин:
 (4.70)
(4.70)
Тогда дифференциальное уравнение (IV.16), начальное (IV.2) и граничное (IV.3) условия в безразмерном виде будут:
 (4.71)
(4.71)
При  , (4.72)
, (4.72)
 (4.73)
(4.73)
Интеграл дифференциального уравнения (4.71), удовлетворяющий условиям (4.72) и (4.73) может быть записан в виде
 (4.74)
(4.74)
Таким образом, чтобы осуществить подобие явлений теплопроводности в случае, когда физические параметры зависят от температуры, необходимо и достаточно в геометрически подобных телах реализовать тождественно одинаковое распределение критериев 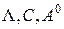 и
и  , т.е. осуществить равенства:
, т.е. осуществить равенства:
 или
или  ;
;
 или
или  ; (4.75)
; (4.75)
 или
или  ;
;
 .
.
Отсюда следует, что при выполнении условий (4.75) во всех сходственных точках модели и образца, т.е. при

и в исходные моменты времени, т.е. при
 ,
,
будет иметь место не только равенство
 ,
,
но такие равенства
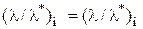 и
и 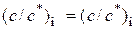 ,
,
т.е. будет обеспечено подобие не только температурных полей, но также и подобие полей физических параметров  и
и  .
.






