ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ АНИЗОТРОПНОГО ТЕЛА В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
Некоторые сведения о криволинейных координатах в пространстве
Как известно, положение какой-либо точки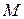 
в пространстве однозначно может быть определено ее радиусом-вектором 
относительно некоторой неподвижной точки 
. В прямоугольных – декартовых координатах для имеем
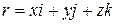(1.1)
где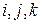 
– единичные векторы.
В общем случае, в задачах теории оболочек выгодно положение какой-либо точки 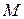, имеющей радиус-вектор , определить не тремя декартовыми координатами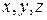 
, а тремя какими-либо другими величинами 
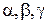, которые однозначно определяют положение точки 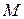в пространстве и называются криволинейными координатами и как функции в декартовых координатах имеют вид
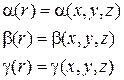(1.2)
Обратно, так как радиус-вектор любой точки 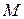пространства является вполне определенным, когда заданы 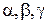, то он является функцией от этих независимых переменных, следовательно, и компоненты этого радиуса-вектора будут функциями криволинейных координат
, 
, 
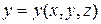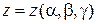. (1.3)
Согласно (1.2), предполагая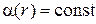 
, 
, 
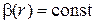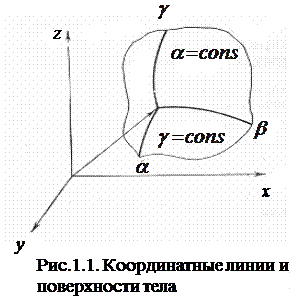
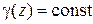, получим три семейства поверхностей. Через каждую точку 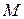пространства проходит по одной поверхности из каждого такого семейства: эти поверхности называются координатными поверхностями. Линии пересечения координатных поверхностей называются координатными линиями (рис.1.1).
В указанной триортогональной системе криволинейных координат для квадрата линейного элемента пространства имеем
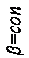
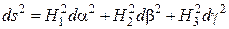, (1.4)
где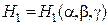 
, 
,
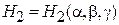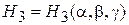в общем случае ортогональных криволинейных коорди-нат являются функциями переменных 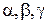и называются коэффициентами Ляме.
При заданных соотношениях (1.3) для данной системы координат ко-эффициенты Ляме определяются посредством следующих формул:
, 
,
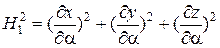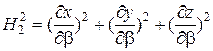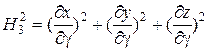. (1.5)
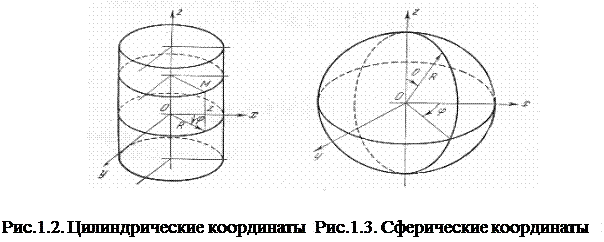
Например, в цилиндрических координатах при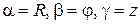 
, когда соотношения (1.3) имеют вид (рис.1.2)
,
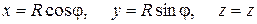из (1.5) для коэффициентов Ляме получим
.
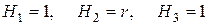В сферических координатах (рис.3) при 
, когда соотношения (1.3) имеют вид
,
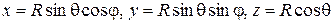из (1.5) имеем
.
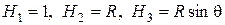В декартовых прямоугольных координатах 
формула для квадрата линейного элемента имеет вид
,
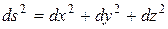в силу чего для коэффициентов Ляме имеем
.
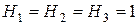Составляющие деформации и дифференциальные уравнения равновесия в триортогональной системе криволинейных координат
Пусть сплошное тело, отнесенное к триортогональной системе координат 
, под действием каких-либо сил критериевой деформации. Тогда какая-либо точка 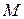, принадлежащая телу и имеющая координаты , получит перемещение, которое может быть представлено следующими тремя проекциями вектора полного перемещения на направления касательных к координатным линиям
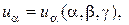
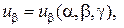
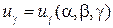. (1.6)
Все эти величины называются перемещения точки 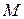. За положительные примем перемещения 
, 
, 
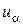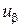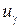, направленные в сторону положительных изменений соответствующих переменных .
Деформационное состояние сплошного трехмерного тела в окрестности точки 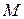характеризуется шестью составляющими деформации.
Из этих составляющих три, которые обозначаются через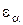 
, 
, 
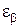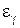, представляют соответственно относительные деформации удлинения по трем взаимно перпендикулярным направлениям , а остальные три, которые обозначаются через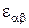 
, 
, 
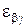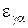, представляют соответственно деформации сдвига, происходящие в трех взаимно перпендикулярных плоскостях, являющихся касательными плоскостями в точке 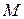к трем взаимно перпендикулярным координатным поверхностям
, 
, 
.
Составляющие деформации 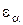, , 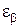… 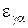связаны с перемещениями 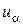, , 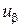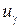из точки 
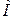посредством следующих формул:
;
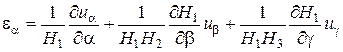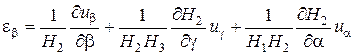; (1.7)
;
;
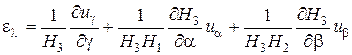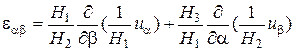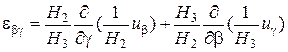; (1.8)
;
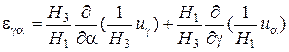Напряженное состояние в какой-либо точке 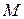сплошного трехмерного тела, как известно, характеризуется тензором напряжений, который определяется девятью компонентами. Из этих компонентов три являются нормальными напряжениями, которые действуют по трем взаимно перпен-дикулярным направлениям координатных линий 
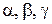, и шесть – касательными напряжениями, действующими в трех взаимно перпендикулярных плоскостях, являющихся касательными плоскостями в точке 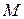к трем взаимно перпендикулярным координатным поверхностям (рис. 1.4) , , . В силу парности касательных напряжений число независимых напряжений равно не девяти, а шести.
, 
, 
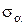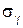– нормальные напряжения, подстрочные индексы которых показывают направления внешней нормали к той площадке, к которой данные напряжения относятся.
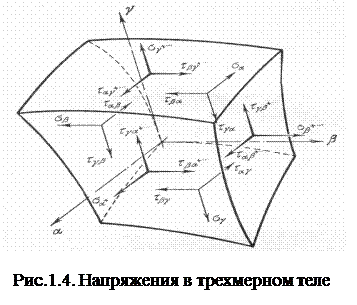
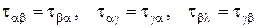– касательные напряжения, первые подстрочные индексы которых показывают направление, в котором действует данное касательное напряжение, а вторые индексы – направления внешней нормали к площад-ке, к которой приложено данное напряжение.
Все напряжения счита-ются положительными, если они, будучи приложенными к площадкам с положитель-ными внешними нормалями, действуют по направлению соответствующих положи-тельных внешних нормалей (рис.1.4).
Если рассмотренное сплошное трехмерное тело находится в равновесии, то условия равновесия дифференциального элемента тела в продольно выбранной триортогональной системе криволинейных координат представляются следующими тремя дифференциальными уравнениями:
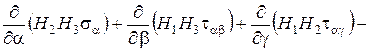
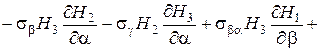
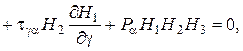(1.9)
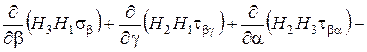
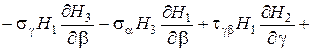
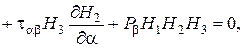(1.10)
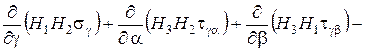
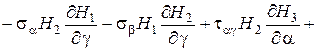
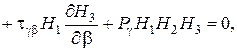(1.11)
где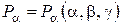 
, 
, 
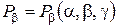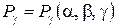представляют соответствующие проекции объемной силы на направления касательных к координатным линиям 
.
