Пример с движением точки по закону s (t) = 3t2 таким образом, если s (t) = 3t2, то на отрезке времени [t; t + h]
vср. = s(t+h)−s(t)/ h= (t+h)2−3 t2)/ h = 6th+3t2/h=6t+3h.
Очевидно, что при уменьшении h(h→0) значения средней скорости приближаются к значению мгновенной скорости, т. Е. v(t)= lim h→0 vср. = lim h→0(6t+3h)=6t=6⋅1=6.
В математическом анализе уже для любой функции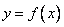 
рассматривают важную величину:
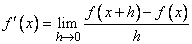,(1) которую называют производной функции 
.
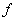Производная, таким образом, играет роль скорости изменения зависимой переменной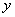 
по отношению к изменению независимой переменной 
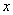; последняя теперь уже не обязана иметь физический смысл времени.
Значение производной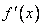 
зависит от значения аргумента 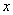, поэтому, как и в случае скорости, производная 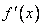некоторой функции 
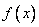сама является функцией переменной .
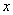Например, если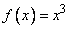 
, то
;
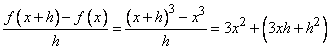далее, при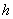 
, стремящемся к нулю, величина, стоящая в последних скобках, стремится к нулю, а вся правая часть при этом стремится к значению 
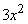. Мы нашли таким образом, что если 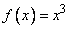, то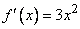 
.
В формуле (1) величину 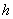разности 
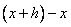называют приращением аргумента функции и часто обозначают символом 
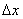(читается: дельта икс), а разность 
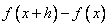обозначают обычно через 
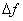(или, более полно через 
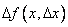) и называют приращением функции, соответствующим данному приращению аргумента. В этих обозначениях выражение (1) приобретает вид:
,
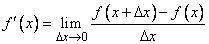или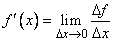 
.
Таким образом, значение 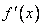производной функции 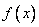в точке 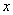- это предел отношения приращения функции 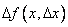, соответствующего смещению 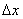от точки 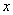, к приращению 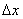аргумента 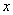, когда 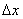стремится к нулю.
Правила дифференцирования. Формулы для нахождения производной.
В дифференциальном исчислении выводятся также следующие общие правила дифференцирования:
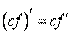(вынесение постоянного множителя);
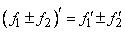(дифференцирование суммы и разности функций);
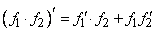(дифференцирование произведения функций);
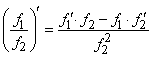(дифференцирование частного функций).
| Формулы для нахождения производной | |
|  , 
|
| 
|
 
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
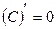
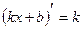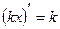
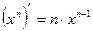
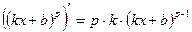
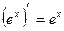
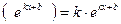
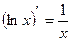
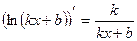
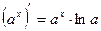
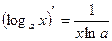
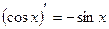
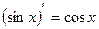
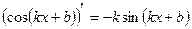
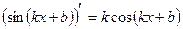
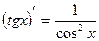
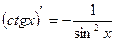
| Правила дифференцирования | |
1. Производная суммы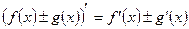 
| 3. Производная произведения
|
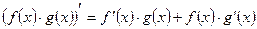
2. Постоянный множитель можно выносить за знак производной
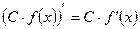
| 4. Производная частного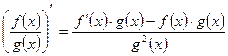 
|
| Y =(e x | + 5 cos x)⋅3 x. | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| Пример 1. Найти производную функции: | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Решение: | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Применяем | формулу | для | производной | от | произведения | функций: | |||||||||||||||||||||||||||||||||||||||||||||||
| (u ⋅ v)′ | = u ′⋅ v + v ′⋅ u, при этом учитываем, что: (ex)′ | = e x; | (cos x)′ = −sin x. | ||||||||||||||||||||||||||||||||||||||||||||||||||
| y ′ =((e x | + 5cos x)⋅3 | x)′=(e x | + 5cos x)′ ⋅3 | x +(e x +5cos x)⋅(3 x)′ =(e x −5sin x)⋅3 x + | |||||||||||||||||||||||||||||||||||||||||||||||||
| + (e x + 5cos x)⋅ | x − | ||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 2.
Найти производную функции: y = x 2 + 5 ln x
Решение: Применяем формулу для производной от суммы функций.
y ¢= (x 2 + 5 ln x)¢= (x 2)¢+ 5(ln x)¢= 2 x + 5/х.