ЭПЮР № 1
ТОЧКА, ПРЯМАЯ, ПЛОСКОСТЬ
Цель работы: решение метрических и позиционных задач начертательной геометрии без применения способов преобразования комплексного чертежа.
Объем и оформление работы. Выполнить графическое решение задачи на формате АЗ (297х420) в масштабе 2:1. Координаты точек взять из таблицы 1. Вариант задания соответствует сумме двух последних цифр студенческого билета или зачетной книжки. Чертежи и надписи выполнить соответствии с ГОСТ 2.303-68 (линии) и ГОСТ 2.304-68 (шрифты чертежные). Исходные данные и результат вычертить сплошной основной линией. Линии построения, оси, линии связи, вспомогательные линии – сплошной тонкой линией. Обозначения точек, прямых, плоскостей, алгоритм решения выполнить шрифтом размера 5. В правом верхнем углу поместить таблицу с координатами точек, заполнить ее цифрами шрифтом 7.
Общие сведения. Решение задач эпюра осуществляется на основании следующих положений элементарной и начертательной геометрии.
1. Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым плоскости. На эпюре проекции перпендикуляра перпендикулярны одноименным проекциям линий уровня n ┴ ∆ ABC, если
n1 ┴ h1, n2 ┴ f2 (рис.l).
2. Две плоскости параллельны между собой, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. При этом проекции параллельных прямых параллельны(рис.2).
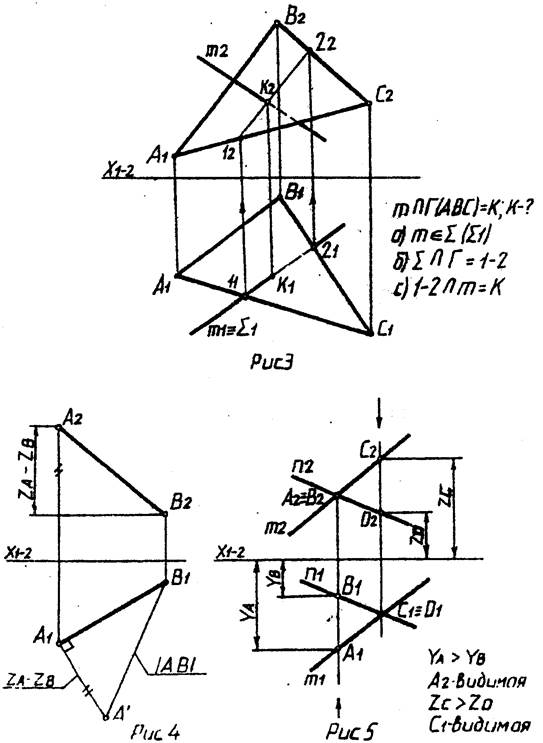
3. Чтобы найти точку пересечения прямой с плоскостью необходимо: а) через прямую провести вспомогательную проецирующую плоскость; б) найти линию пересечения вспомогательной и заданной плоскостей; в) определить искомую точку на пересечении полученной линии и данной прямой (рис.3).
Таблица 1
Координаты точек А, В, С, D в миллиметрах по вариантам заданий
| Точки | № варианта | X | Y | Z | № варианта | X | Y | Z | № варианта | X | Y | Z | № варианта | X | Y | Z |
| А | 1 | 2 | 3 | 4 | ||||||||||||
| В | ||||||||||||||||
| С | ||||||||||||||||
| D | ||||||||||||||||
| А | 5 | 6 | 7 | 8 | ||||||||||||
| В | ||||||||||||||||
| С | ||||||||||||||||
| D | ||||||||||||||||
| А | 9 | 10 | 11 | 12 | ||||||||||||
| В | ||||||||||||||||
| С | ||||||||||||||||
| D | ||||||||||||||||
| А | 13 | 14 | 15 | 16 | ||||||||||||
| В | ||||||||||||||||
| С | ||||||||||||||||
| D | ||||||||||||||||
| А | 17 | 18 | 19 | 20 | ||||||||||||
| В | ||||||||||||||||
| С | ||||||||||||||||
| D | ||||||||||||||||
| А | 21 | 22 | 23 | 24 | ||||||||||||
| В | ||||||||||||||||
| С | ||||||||||||||||
| D | ||||||||||||||||
| А | 25 | 26 | 27 | 28 | ||||||||||||
| В | ||||||||||||||||
| С | ||||||||||||||||
| D | ||||||||||||||||
| А | 29 | 30 | 31 | 32 | ||||||||||||
| В | ||||||||||||||||
| С | ||||||||||||||||
| D |

4. Для определения величины отрезка способом прямоугольного треугольника необходимо через конец одной из проекций отрезка провести под прямым углом линию и отложить на ней разность координат концов отрезка, взятых с другой проекции. Гипотенуза будет характеризовать величину отрезка (рис.4).
5. Для определения видимости проекций пользуются конкурирующими точками. На горизонтальной плоскости проекций видимой из конкурирующих точек является та, которая имеет большую высоту, т.е. координату Z. На фронтальной плоскости проекций видимой является точка с большей глубиной, т.е. координатой Y (рис.5).
Задача. Определить величину угла между прямой AD и плоскостью треугольника АВС (рис.6).
Приведем поэтапное решение задачи.
Искомый угол φ - это угол между прямой AD и ее проекцией на плоскость треугольника АВС
1. В треугольнике АВС проведем горизонталь h (h2 h1) и фронталь f (f1, f2). B є h; h2 || OX; A є f; f1 || OX.
2. Из точки пересечения горизонтали и фронтали N (N1, N2) восставим перпендикуляр n (n1, n2) к плоскости треугольника АВС, n ┴ ∆ ABC, если n1 ┴ h1, n2 ┴ f2.
3. Из точки D (D1, D2) проведем прямую m, параллельную перпендикуляру n.
4. Найдем точку пересечения прямой m с плоскостью треугольника АВС. Для этого проведем через прямую m вспомогательную горизонтально проецирующую плоскость Σ (Σ1). Построим линию пересечения плоскости Σ с плоскостью треугольника АВС. Σ ∩ ∆ АВС=3-4. На пересечении линии 3-4 и прямой m получим искомую точку М.
5. Соединим точки A и М - АМ (A1M1• A2M2). Определим величины отрезков АМ и DМ способом прямоугольного треугольника A'М1=|AМ|, D'M1= |DM|.
6. Пострoим по двум катетам АМ и MD (на свободном месте листа А3) прямоугольный треугольник AМD.
Угол DАМ есть искомый угол φ.
7. Определим видимость элементов, используя конкурирующие точки.
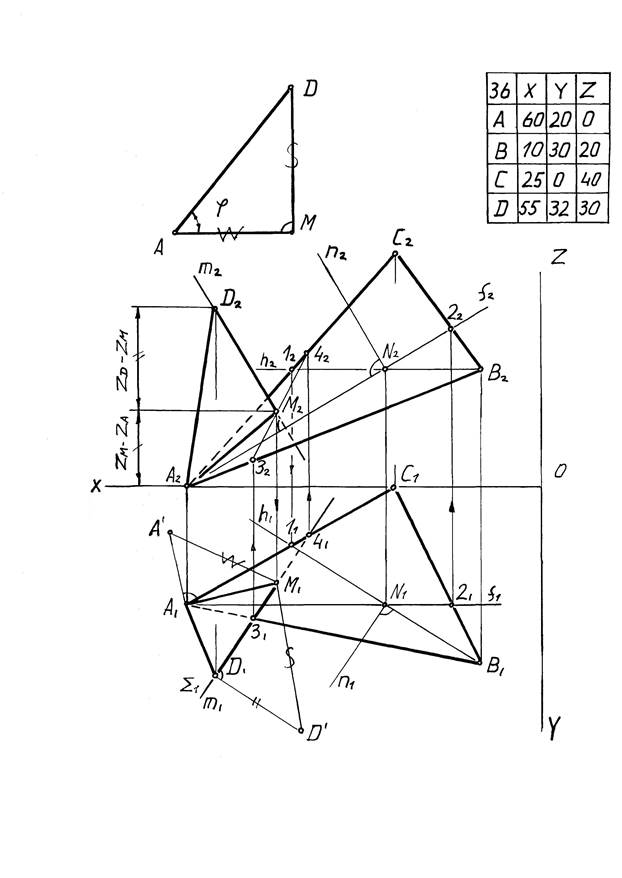
Рис.6.
ЭПЮР №2
СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА.
Цель работы. изучение способов преобразования чертежа.
Объем и оформление работы. Выполнить пять задач на двух или трех листах формата А3 (297х420) в масштабе 1:1. Координаты точек взять из таблицы 1. Вариант задания соответствует сумме двух последних цифр студенческого билета или зачетной книжки. Чертежи и надписи выполнить в соответствии с ГОСТ 2.303-68 (линии) и ГОСТ 2.304-68 (шрифты чертежные). Исходные данные и результат вычертить сплошной основной линией. Линии построения, оси, линии связи и вспомогательные линии – сплошной тонкой линией. Обозначения точек, прямых, плоскостей, алгоритм решения выполнить шрифтом размера 5.
Общие сведения. Решение задач эпюра осуществляется применением способов преобразования чертежа.
Пользуясь способами преобразования чертежа, можно перейти от общих положений прямых линий и плоских фигур к частным. Достигается это:
1) заменой системы плоскостей проекций на новую систему плоскостей проекций, чтобы объект, оставаясь неподвижным, оказался в частном положении по отношению к новой системе;
2) перемещение объекта в пространстве (способ вращения, параллельного перемещения).
Задача 1. Определить величину двугранного угла, образованного треугольниками ABC и ABD способом замены плоскостей проекций (рис. 7).
Двугранный угол измеряется линейным углом, если его спроецировать на плоскость, перпендикулярную к ребру AB. Необходимо сделать две замены плоскостей проекций. При первой замене переходим от системы П2/П1 с осью Х1-2 к системе П1/П4 с осью Х1-4. Выберем П4 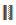 AB.
AB.
Тогда ось Х1-4 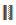 A1B1 . Находим новые проекции точек A4, B4,C4,D4. Для этого проведем от проекций A1, B1,C1,D1 линии связи перпендикулярно к оси Х1-4 и отложим на них от новой оси Х1-4 расстояния, замеренные от заменяемой оси Х1-2 до заменяемых проекций A2, B2,C2,D2 . Соединяем соответствующие построенные проекции точек. Проекция A4 B4 будет характеризовать величину ребра AB.
A1B1 . Находим новые проекции точек A4, B4,C4,D4. Для этого проведем от проекций A1, B1,C1,D1 линии связи перпендикулярно к оси Х1-4 и отложим на них от новой оси Х1-4 расстояния, замеренные от заменяемой оси Х1-2 до заменяемых проекций A2, B2,C2,D2 . Соединяем соответствующие построенные проекции точек. Проекция A4 B4 будет характеризовать величину ребра AB.
При второй замене переходим от системы П1/П2 с осью Х1-4 к системе П4/П5 с осью Х4-5 . Выбираем П5 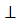 П4 и П5
П4 и П5 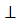 AB;ось Х4-5
AB;ось Х4-5
будет перпендикулярно к A4B4. Находимновые проекции точек A5, B5,C5,D5 . Для этого проведем от проекций A4, B4,C4,D4 проведем линии связи перпендикулярно к Х4-5 и отложим на них от новой оси Х4-5 расстояния замеренные от заменяемой оси Х1-4 до заменяемых проекций A1, B1,C1,D1 . Ребро AB

Рис.7.
проецируется в точку A5≡B5. Соединяем ее с D5 и C5, получим величину искомого двугранного угла  C5A5D5 =φ.
C5A5D5 =φ.
Задача 2. Определить кратчайшее расстояние между двумя скрещивающимися прямыми AB и CD способом замены плоскостей проекций.Найтипроекции этого отрезка (рис.8).
Кратчайшим расстоянием между двумя скрещивающимися прямыми является их общий перпендикуляр. Если одна из прямых будет перпендикулярна к плоскости проекций, то она спроецируется на нее точкой. Перпендикуляр, построенный из этой точки на проекцию второй прямой, будет искомой величиной. Необходимо сделать две замены плоскостей проекций, аналогично тем, что сделали в предыдущей задаче
1. Х1-2 
 Х1-4
Х1-4 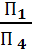 ; П4
; П4 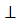 П1 ; П4
П1 ; П4  AB; Х1-4
AB; Х1-4  A1B1,
A1B1,
2. Х1-4 
 Х4-5
Х4-5  ; П5
; П5  П4 ; П5
П4 ; П5  AB; Х4-5
AB; Х4-5  A4B4,
A4B4,
При построении новых проекций точек расстояние от заменяемой оси до заменяемой проекции откладывается по линиям связи от новой оси. Из
A5 ≡B5 - построим перпендикуляр на C5D5. Это и есть величина кратчайшего расстояния между скрещивающимися прямыми AB и CD. Остальные проекции точек K и L определяем по линиям связи и принадлежности K  C4D4, L4K4
C4D4, L4K4  Х4-5 , L4
Х4-5 , L4  A4B4 и т.д.
A4B4 и т.д.
Задача 3. Определить расстояние от точки D до плоскости треугольника ABC методом вращения вокруг проецирующей прямой. Определить проекции основания перпендикуляра (рис. 9).
Расстояние от точки D до плоскости определяется длиной перпендикуляра, проведенного из точки D до плоскости треугольника ABC. Если плоскость ABC сделать проецирующей, то этот перпендикуляр спроецируется на соответствующую плоскость проекций без искажения.
Сделаем плоскость треугольника ABC фронтально проецирующей, вращая ее вокруг горизонтально проецирующей оси i (i1,i2), которую выберем проходящей через точку C(C1,C2). В плоскости треугольника ABC проведем горизонталь h(h2, h1). Повернем ее до положения перпендикулярной к фронтальной плоскости проекций. Проекция центра вращения О1 совпадает с i1, радиус вращения R равен O111 . Построим треугольник A1B1C1 , затем повернутую проекцию точки D-D1 . Построение проекций A1, B1,C1,D1 сделаем засечками относительно проекции горизонтали h. Фронтальные проекции точек A2,B2,C2,D2 будут
перемещаться по горизонтальным линиям, на пересечении их с линиями связи, приведенными из A1,B1,C1,D1. В итоге получается А12,B12,С12, D12. 
Рис.8.
Соединим А12,B12,С12. Из D12. построим перпендикуляр к А12,B12,С12. Обозначим проекцию его основания Е12. Отрезок D12 Е12 - искомое расстояние от точки D до плоскости треугольника ABC. Проекцию E1 находим на пересечении линии связи, проведенной из Е12, с перпендикуляром, построенного из D1 к проекции h1. Проекции E1 и E2 находим обратным вращением.
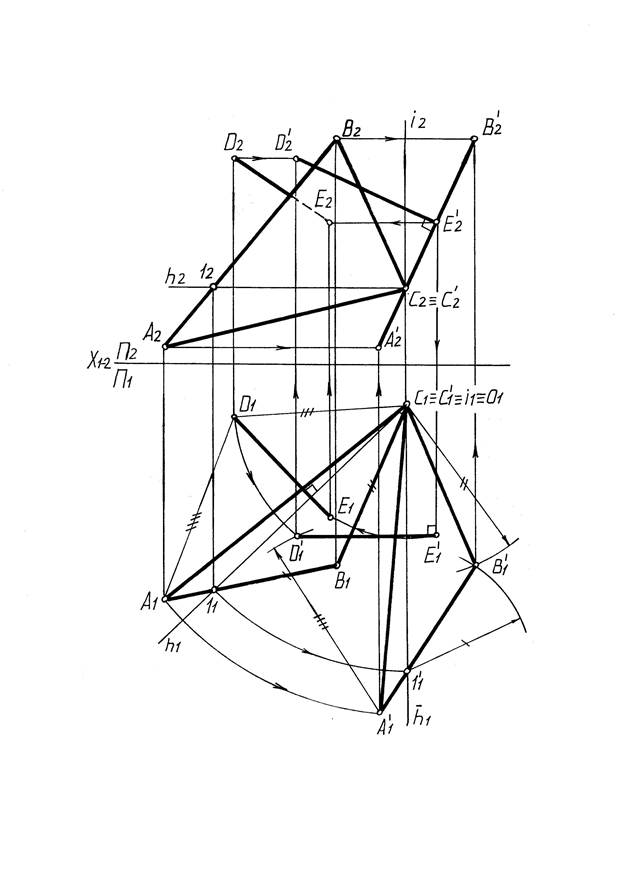
Рис.9.
Задача 4. Определить величину треугольника ABC методом вращения вокруг линии уровня (рис. 10).

Рис.10.
Повернем треугольник ABC вокруг горизонтали h, которая будет являться осью вращения. Точка С останется неподвижной С1  С11 .
С11 .
Рассмотрим вращение точки В. Плоскость θ(θ1) перпендикулярна оси вращения (θ1  h1 ). Центр вращения О(О1,О2) определяется в пересечении оси вращения с плоскостью вращения
h1 ). Центр вращения О(О1,О2) определяется в пересечении оси вращения с плоскостью вращения 
 h =О. Радиус вращения – ОВ. Величину ОВ определяем способом прямоугольного треугольника, отложив на перпендикуляре к В1О1 отрезок В0В1, равный разности высот точек В и О - ∆ZВО. Гипотенуза В0О1 будет характеризовать величину ВО, которую отложим от О1 на следе – проекции θ1. Получим проекцию В11 повернутой точки В.
h =О. Радиус вращения – ОВ. Величину ОВ определяем способом прямоугольного треугольника, отложив на перпендикуляре к В1О1 отрезок В0В1, равный разности высот точек В и О - ∆ZВО. Гипотенуза В0О1 будет характеризовать величину ВО, которую отложим от О1 на следе – проекции θ1. Получим проекцию В11 повернутой точки В.
Через А1 проведем след-проекцию ∑1 плоскости вращения точки А. Соединим проекцию В 1 повернутой точки В с проекцией 11 неподвижной точки 1 и продолжим эту линию до пересечения с ∑1. Это будет проекция А11 повернутой точки А. Соединив A11, B11,C11 , получим натуральную величину треугольника АВС.
Задача 5. Определить натуральную величину угла между прямой AD и плоскостью треугольника АВС методом плоскопараллельного перемещения и вращения вокруг проецирующей прямой (рис.11).
Угол между прямой и плоскостью измеряется углом между самой прямой и ее проекцией на данную плоскость.
Для решения задачи сделаем плоскость треугольника сначала проецирующей, затем плоскостью уровня. Для этого проведем в плоскости горизонталь h (h2, h1) через точку С, разместим ее перпендикулярно фронтальной плоскости h (h1,h2), построим относительно h1 (засечками) треугольник A11 B11C11 , равновеликий A1 B1C1, а затем проекцию D11 (также двумя засечками). Фронтальные проекции точек A2,B2,C2,D2 переместятся по горизонтальным линиям до пересечения с линиями связи, проведенными из A1,B1,C1, D1 . Полученные проекции A12, B12,C12 лежат на одной прямой. Соединим D12 с А12.
При втором перемещении фронтальная проекция сохраняет вид и величину. Разместим A2B2C2 параллельно горизонтальной плоскости проекции и обозначим A22B22C22, затем построим D22 (засечками). Горизонтальные проекции A1,B1,C1,D1 переместятся в плоскостях, параллельных плоскости П2, и будут находится на линиях связи, проведенных из A22, B22,C22,D22 . Обозначим и соединим A21 B21C21 и D21 с A21 .
Проекция A1 B1C1 - есть величина треугольника АВС. Повернем DA вокруг горизонтально проецирующей оси i (i1,i2), проходящей через точку А, до положения, параллельного плоскости П2. Проекции точки D в новом положении обозначим D31 и D32. Угол D32A32B22 есть искомый угол между прямой AD и плоскостью треугольника ABC.

Рис.11.






