Тема 2.1. Определенный интеграл

 

Пусть на отрезке [a,b] задана функция , и отрезок разбит на n элементарных отрезков точками x₀, x₁, …, x_n: a= x₀ < x₁ <…< x_n=b, Dx=x_i-x _i-1/

Определенным интегралом от функции не отрезке [a,b] называется предел интегральной функции при Dx®0, а функция f(x) называется интегрируемой на отрезке [a,b].

Число a называется нижним пределом интегрирования, а число b – его верхним пределом.

Геометрический смысл определенного интеграла заключается в следующем. Если функция неотрицательна на отрезке [a,b], где a<b, то численно равен площади под кривой на [a,b]. Для нахождения определенного интеграла пользуются формулой Ньютона-Лейбница:

, (1)

где F(a) и F(b) первообразные для f(x) в точках a и b. Первообразной функцией для функции на промежутке Х называется функция F(x), если в каждой точке x этого промежутка .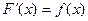

Однако применение формулы Ньютона-Лейбница на практике связано с трудностями, поэтому используют численные методы, позволяющие найти приближенное значение искомого интеграла. Рассмотрим два метода:

- метод прямоугольников – как суммы элементарных прямоугольников

- (2)

Суть метода прямоугольников в том, что на каждом из участков разбиения [ x_i-1, x_i ] участок кривой заменяется отрезком прямой, параллельным оси абсцисс. Тогда определенный интеграл приближенно равен сумме площадей прямоугольников на каждом участке разбиения.

- метод трапеций – как суммы элементарных трапеций

- (3)

метод трапеций является более точным, т.к. каждый участок кривой заменяется не прямыми, а хордами, стягивающими концевые точки. Тогда каждое слагаемой интегральной суммы будет равно площади трапеции с основаниями f(x_i) и f(x_i-1) и высотой Dх.

Пример. Методом прямоугольника и методом трапеции найти с шагом Dх=0,1. Заметом, что этот интеграл легко вычислить аналитически:

Решение1.

На листе Excel составляем таблицу данных. Заполняем значение аргумента (в ячейки А1:А32) и значение функции () (в ячейки В1:В32) (см. Декартова система координат, Пример 1).

Введем слово интеграл в ячейку А33 и в соседней ячейке формулы =0,1*, затем вызываем Мастер функций и в категории Математические выбираем функцию СУММ. Нажимаем ОК. В диалоговое окно Мастера функции вводим диапазон суммирования – значения функции (В2:В32). В ячейке В33 появляется приближенное значение интеграла (9,455).

Ошибка в методе прямоугольников составила 0,455.

Решение 2.

Используем метод трапеции. Для этого в ячейку А34 введем слово интеграл 2. В соседнюю ячейку вводим формулу =0,1*((В2+В32)/2+) затем вызываем функцию СУММ. Нажимаем ОК. В диалоговое окно Мастера функции вводим диапазон суммирования – значения функции (В3:В31). В ячейке В34 появляется значение =9,005. В данном случае ошибка метода составляет 0,005, что вполне приемлемо.

 

Упражнения.

Найти при помощи метода прямоугольника и трапеции определенные интегралы:

1. с шагом Dх=0,1.
2. с шагом Dх=0,1.
3. с шагом Dх=0,1.