Решение задач – одна из наиболее активных форм обучения и самостоятельной работы учащихся дневной и заочной формы обучения.
Решение задач рекомендуется вести в следующем порядке:
а) записывается условие задачи, которое сопровождается чертежом или схемой;
б) после разбора условия и содержания задачи намечается план ее решения;
в) решение проводится по этапам с указанием цели каждого этапа;
г) выписывается формула, используемая для решения на данном этапе, после чего в нее подставляют числовые значения величин; промежуточные результаты решения выписываются на поля и подчеркиваются;
д) должны указываться размерности вычисляемых величин;
е) после решения задачи оценивается правдоподобность полученного результата.
Номер варианта соответствует номеру по учебному журналу
| № варианта контрольной | № по журналу |
| 1,16 | |
| 2,17 | |
| 3,18 | |
| 4,19 | |
| 5,20 | |
| 6,21 | |
| 7,22 | |
| 8,23 | |
| 9,24 | |
| 10,25 | |
| 11,26 | |
| 12,27 | |
| 13,28 | |
| 14,29 | |
| 15,30 |
Для решения задачи 1 необходимо знать:
- закон Ома для электрической цепи;
- первый закон Киргофа;
- методику определения полного сопротивления цепи при смешанном соединении сопротивлений и ознакомиться с решением примера 1-11, данным в учебнике Попова и Николаева.
Задача 2 относится к неразветвленным цепям переменного тока. Перед решением ознакомиться с темой 5, учебник Свириденко Э.А. и Китунович Ф.Г.
Пример:
Последовательно с катушкой, активное сопротивление которой r1=10 Ом и индуктивное х 
= 10 Ом, включен потребитель, обладающий активным сопротивлением r2=1 Ом и емкостным х 
= 4 Ом (рис.1, а), к цепи приложено напряжение U=120 В (действующее значение).
Определить:
- полное сопротивление цепи;
- коэффициент мощности цепи;
- силу тока;
- напряжения на каждом сопротивлении;
- активную, реактивную и полную мощности цепи.
Построить в масштабе векторную диаграмму.
Решение:
1) Полное сопротивление цепи
2) Коэффициент мощности цепи
а)
Рисунок 1а
б) Масштаб:
1 см – 4 А
 |
1 см – 20 В
Рисунок 1б
3) Сила тока в цепи
4) Напряжение на сопротивлениях цепи
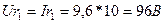
5) Активная мощность
6) Реактивная мощность
Здесь sin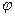 
= 0.48, который определяется по таблице тригонометрических величин по известному значению cos 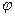= 0.88
7) Полная мощность
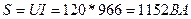
или
8) Построение векторной диаграммы начинаем с выбора масштабов для тока и напряжения. Задаемся масштабом по току: 1 см - 4А и масштабом по напряжению: в 1см - 20В.
Построение векторной диаграммы (рис.1б) начинаем с вектора тока.
Откладываем по горизонтали вектора тока.
Вдоль вектора тока откладываем векторы напряжения на активных сопротивлениях r1 и r2.
и 
К концу вектора Ur откладываем в сторону опережения вектора тока на 90° вектор напряжения U на индуктивном сопротивлении. Длина вектора
Из конца вектора U откладываем в сторону отставания от вектора тока на 90° вектор напряжения на емкостном сопротивлении. Длина вектора
Геометрическая сумма векторов Ur 
, Ur 
, U и U представляет полное напряжение U, приложенное к цепи. Так как длина вектора равна 6 см, то величина напряжения составит
Задача 3 относится к трехфазным цепям. Предварительно следует повторить материал темы 6 учебника Свириденко Э.А. и Китуновича Ф.Г.
Пример:
В каждую фазу трехфазной четырех проводной цепи включили сопротивления так, как показано на рис. 2. Величины сопротивления даны на рисунке. Линейное напряжение сети U=380 В.
Определить: линейные токи; углы сдвига фаз; активную, реактивную и полную мощности трех фаз.
Решение:
1) Полное сопротивление фаз
2)Углы сдвига фаз
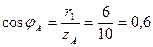
(опережающий)
(отстающий)
3) Линейные (фазные) токи
Здесь фазное напряжение
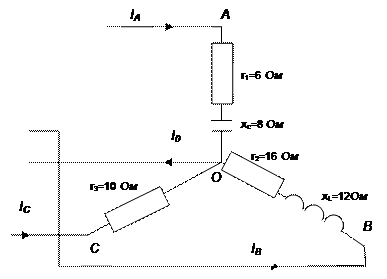
Рисунок 2
4)Активная мощность потребляется только активными сопротивлениями. Поэтому
5) Реактивная мощность потребляется только реактивными сопротивлениями. Поэтому 
Знак минус показывает, что реактивная мощность системы носит емкостный характер.
6) Полная мощность
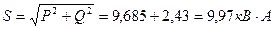
Задача 4 относится к асинхронным двигателям. Необходимо изучить материал темы 8 учебника Свириденко Э.А. и Китунович Ф.Г.
Пример:
Асинхронный двигатель с короткозамкнутым ротором имеет величины:
- номинальная мощность Рн = 12 кВт;
- номинальное напряжение Uн = 380 В;
- число оборотов n н = 1480 об/мин;
- КПД 
н = 0,88; cos 
= 0,85;
- краткость пускового тока 
= 6,5;
- перегрузочная способность 
= 1,8.
Определить:
- потребляемую мощность;
- номинальный и максимальный моменты;
- пусковой ток;
- номинальное скольжение.
- Как изменится пусковой ток, а также номинальный и максимальный моменты при снижении напряжение в сети на 10%?
Решение:
1) Потребляемая мощность
2) Номинальный момент
3) Максимальный момент
4) Номинальный ток
Номинальный ток двигателя определяется потребляемой мощностью, которая равна номинальной, деленной на КПД, т. е.
5) Пусковой ток
6)Номинальное скольжение
При 
скорость поля равна
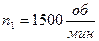
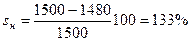
Задача 5 относится к машинам постоянного тока. Тема 9 учебника Свириденко Э.А. и Китунович Ф.Г.
Пример:
Двигатель постоянного тока при номинальной мощности Рн=68 кВт вращается со скоростью п н=1460 об/мин. Сила тока в цепи якоря I 
=346 А; сопротивление обмотки якоря rя = 0,023 Ом. Номинальное напряжение сети Uн = 220 В.
Определить:
- противо-ЭДС в обмотке якоря;
- электромагнитную мощность;
- номинальный и электромагнитный моменты и момент холостого хода.
Решение:
