ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ
ХАНТЫ-МАНСИЙСКОГО АВТОНОМНОГО ОКРУГА – ЮГРЫ
ГОУ ВПО «СУРГУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ХАНТЫ-МАНСИЙСКОГО АВТОНОМНОГО ОКРУГА – ЮГРЫ»
Кафедра высшей математики
И.В. Шапошникова
МАТЕМАТИКА
Методические указания
Сургут
Издательский центр СурГУ
201 6
И.В. Шапошникова.
Математика: Методические указания для студентов по направлению – ГМУ
Методические указания предназначены для студентов первого курса заочного отделении по направлению «Государственное муниципальное управление» и содержит программу курса математики, утверждённую методическим Советом политехнического института СурГУ, общие рекомендации студенту-заочнику по изучению данной дисциплины, список литературы, контрольные задания (10 вариантов) и вопросы для самопроверки по разделам курса. Поскольку издание преследует сугубо учебно-методические цели, то оно носит компилятивный характер.
ОБЩИЕ РЕКОМЕНДАЦИИ СТУДЕНТУ-ЗАОЧНИКУ ПО РАБОТЕ НАД КУРСОМ ВЫСШЕЙ МАТЕМАТИКИ.
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом, которая состоит из изучения материала по учебникам, решения задач, выполнения контрольных работ, ответов на вопросы для самопроверки. В помощь студентам-заочникам кафедра высшей математики СурГУ организует чтение обзорных лекций, консультации в течение семестра и перед экзаменом (зачетом). Кроме того, студент может обращаться к преподавателю с вопросами в письменном или устном виде. Указания студенту по текущей работе даются также в процессе рецензирования контрольных работ. Однако студент должен помнить, что только при систематической и упорной самостоятельной работе помощь кафедры окажется достаточно эффективной.
Завершающим этапом изучения отдельных частей курса математики является сдача экзаменов и зачетов в соответствии с учебным планом.
КОНТРОЛЬНЫЕ РАБОТЫ.
В процессе изучения курса математики студент должен выполнить контрольную работу, главная цель которой – оказать студенту помощь в его работе. Рецензии преподавателя позволяют студенту судить о степени усвоения им соответствующего раздела курса, указывают на имеющиеся у него пробелы. При выполнении контрольной работы студент должен руководствоваться следующими указаниями:
1. Не следует приступать к выполнению контрольного задания, не решив достаточного количества задач по материалу, соответствующему этому заданию. Опыт показывает, что затруднение при решении той или иной задачи контрольного задания вызвано тем, что студент не выполнил этого требования.
2 Контрольную работу следует выполнять в отдельной тетради. Желательно оставлять на каждой странице широкие поля для замечаний рецензента.
3. На обложке тетради должны быть указаны фамилия и инициалы студента, учебный номер (шифр), название дисциплины. В конце работы должны стоять дата её выполнения и подпись студента.
4. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту. Желательно оставлять на каждой странице широкие поля для замечаний рецензента.
5. Решения задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номер задачи. Перед решением задачи надо полностью выписать её условие.
6. Все вычисления должны быть приведены полностью, со ссылками на используемые формулы. Чертежи и графики должны быть выполнены аккуратно, четко, с указанием единиц масштаба и координатных осей.
7. После получения прорецензированной работы студент должен исправить в ней все ошибки. В случае незачета студент обязан в кратчайший срок выполнить все требования рецензента и предоставить исправленную работу на повторное рецензирование (исправления и дополнения к первоначальной работе обязательно выполняются в той же тетради). При отсутствии зачтенной контрольной работы студент не допускается к экзамену.
8. Контрольная работа должна выполняться самостоятельно.
9. По учебному плану в первом семестре студент-заочник обязан выполнить одну контрольную работу по математическому анализу согласно варианту номер которого совпадает с последней цифрой его учебного номера (шифра) (см. табл. 1).
Таблица 1
Рапределение заданий по вариантам.
| Вариант | Номера задач контрольных заданий |
| 1,11,21,31,41,51,61,71,81,91,101 | |
| 2,12,22,32,42,52,62,72,82,92,102 | |
| 3,13,23,33,43,53,63,73,83,93,103 | |
| 4,14,24,34,44,54,64,74,84,94,104 | |
| 5,15,25,35,45,55,65,75,85,95,105 | |
| 6,16,26,36,46,56,66,76,86,96,106 | |
| 7,17,27,37,47,57,67,77,87,97,107 | |
| 8,18,28,38,48,58,68,78,88,98,108 | |
| 9,19,29,39,49,59,69,79,89,99,109 | |
| 10,20,30,40,50,60,70,80,90,100,110 |
ЗАЧЕТЫ И ЭКЗАМЕНЫ
После каждого семестра студент должен сдавать зачет или экзамен. Обычно экзамену или зачету предшествует собеседование студента с преподавателем по выполненной контрольной работе.
На зачете и экзамене от студента требуется знание определений, формулировок и доказательств теорем в объеме программы курса, знание формул и умение решать соответствующие задачи. При подготовке к экзамену рекомендуется повторить учебный материал по учебнику и конспекту.
- ПРОГРАММА ДИСЦИПЛИНЫ “МАТЕМАТИКА”.
- Матрица. Основные определения.
- Основные действия над матрицами и их свойства.
- Определители матриц и их свойства. Миноры, дополнительные миноры, алгебраические дополнения.
- Обратная матрица.
- Базисный минор матрицы. Ранг матрицы.
- Матричный метод решения систем линейных уравнений.
- Метод Крамера решения систем линейных уравнений.
- Произвольная система линейных алгебраических уравнений. Основные определения. Однородная СЛАУ. Теорема Кронекера-Капелли.
- Метод Гаусса – универсальный метод решения СЛАУ.
- Векторы на плоскости и в пространстве. Основные определения.
- Линейные операции над векторами и их свойства.
- Линейная зависимость векторов.
- Базис на плоскости и в пространстве. Координаты вектора в базисе.
- Прямоугольная декартова система координат. Длина вектора и линейные операции над векторами в координатах.
- Скалярное произведение векторов.
- Уравнение линии на плоскости. Общее уравнение прямой на плоскости. Частные случаи.
- Уравнение прямой по точке и направляющему вектору. Уравнение прямой, проходящей через две точки.
- Угловой коэффициент прямой. Уравнение прямой по точке и угловому коэффициенту. Уравнение пучка прямых.
- Угол между прямыми на плоскости. Условия параллельности и перпендикулярности прямых.
- Кривые второго порядка. Общее уравнение кривых второго порядка. Частные случаи.
- Эллипс. Гипербола. Парабола.
- Уравнение поверхности в пространстве. Общее уравнение плоскости. Частные случаи.
- Уравнение плоскости по точке и вектору нормали.
- Уравнение линии в пространстве. Уравнения прямой в пространстве по точке и направляющему вектору (канонические и параметрические уравнения прямой).
- Уравнения прямой в пространстве, проходящей через две точки. Общие уравнения прямой в пространстве.
- Условия параллельности и перпендикулярности плоскостей. Условия параллельности и перпендикулярности прямых в пространстве. Угол между прямыми в пространстве.
- Понятие множества и основные сведения о математической логике.
- Числовые множества. Числовые промежутки.
- Модуль действительного числа и его свойства.
- Понятие функции и способы ее задания.
- Основные характеристики функций.
- Элементарные функции.
- Понятие предела. Предел последовательности.
- Ограниченные, монотонные последовательности. Число е.
- Понятие предела функции. Свойства функций, имеющих предел. Критерий сходимости монотонной функции.
- Предел функции в бесконечности. Односторонние пределы.
- Бесконечно большая функция и ее свойства. Теорема о связи бесконечно малой и бесконечно большой функций.
- Бесконечно малая функция и ее свойства. Теорема о связи предела и бесконечно малой функции.
- Сравнение бесконечно малых функций.
- Замечательные пределы (I и II).
- Определение непрерывности функции в точке. Свойства непрерывных функций. Точки разрыва.
- Функции, непрерывные на отрезке и их свойства.
- Определение производной функции, ее физический и геометрический смысл.
- Понятие дифференцируемости функции. Теорема о связи между понятиями дифференцируемости и непрерывности функции.
- Основные правила дифференцирования. Дифференцирование сложной и обратной функций.
- Производные основных элементарных функций.
- Дифференциал функции и его геометрический смысл. Основные теоремы о дифференциалах (дифференциал суммы, произведения, частного; дифференциал сложной функции).
- Производные и дифференциалы высших порядков.
- Теорема Роля. Теорема Коши. Теорема Лагранжа, ее геометрический смысл и следствия из нее.
- Правило Лопиталя.
- Аналитические признаки возрастания и убывания функции.
- Экстремумы функции. Необходимый признак существования экстремума. Первый и второй достаточные признаки существования экстремума функции.
- Наибольшее и наименьшее значение функции на отрезке.
- Выпуклость, вогнутость кривой. Точки перегиба.
- Общая схема исследования функции и построение графика на примере кривой Гаусса.
- Предельные микроэкономические показатели.
- Эластичность функции и её свойства.
- Эластичность спроса и предложения.
- Максимизация прибыли.

- ЗАДАЧИ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
Решить систему линейных уравнений а) методом обратнй матрицы; б) по формулам Крамера
1.  2,
2, 
3.  4.
4. 
5. 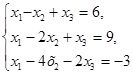 6.
6. 
7.  8.
8. 
9.  10.
10. 
11-20. Исследовать СЛАУ на совместность и в случае совместности решить ее методом Гаусса. Указать число базисных решений и найти одно из них.
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
21-30. Даны координаты точек А, В и С. Для указанных векторов найти: 1) модуль вектора а; 2) скалярное произведение векторов a и b; 3) угол между векторами a и b
21. А(2; -4; 3), В(-3; -2; 4), С(0; 0; -2), а =  , b =
, b = 
22. А(3; 4; -4), В(-2; 1; 2), С(2; -3; 1), а =  , b =
, b = 
23. А(0; 2; 5), В(2; -3; 4), С(3; 2; -5), а =  , b =
, b = 
24. А(-2; -4; -3), В(2; 4; 1), С(1; 4; -2), а =  , b =
, b = 
25. А(5; 4; 4), В(-5; 2; 3), С(4; 2; -5), а =  , b =
, b = 
26. А(3; 4; 1), В(5; -2; 6), С(4; 2; -7), а =  , b =
, b = 
27. А(3; 5; 4), В(4; 2; -3), С(-2; 4; 7), а =  , b =
, b = 
28. А(4; 6; 7), В(2; -4; 1), С(-3; -4; 2), а =  , b =
, b = 
29. А(2; 4; 6), В(-3; 5; 1), С(4; -5; -4), а =  , b =
, b = 
30. А(-1; -2; 4), В(-1; 3; 5), С(1; 4; 2), а =  , b =
, b = 
31-40. Даны четыре точки A, B, C и D. Найти:
1) уравнение плоскости АВС;
2) уравнение прямой АВ;
3) уравнение прямой DM, перпендикулярной к плоскости АВС;
4) уравнение прямой СN, параллельной прямой АВ;
5) уравнение плоскости, проходящей через точку D перпендикулярно к прямой АВ;
6) синус угла между прямой АD и плоскостью АВС;
31. A(1, -2, 7), B(4, 2, 10), C(2, 3, 6), D(5, 3, 7).
32. A(4, 2, 10), B(1, 2, 0), C(3, 5, 7), D(2, -3, 5).
33. A(2, 3, 5), B(5, 3, -7), C(1, 2, 7), D(4, 2, 0).
34. A(5, 3, 7), B(-2, 3, 5), C(4, 2, 10), D(1, 2, 7).
35. A(4, 3, 5), B(1, 9, 7), C(0, 2, 0), D(5, 3, 10).
36. A(3, 2, 5), B(4, 0, 6), C(2, 6, 5), D(6, 4, -1).
37. A(2, 1, 6), B(1, 4, 9), C(2, -5, 8), D(5, 4, 2).
38. A(2, 1, 7), B(3, 3, 6), C(2, -3, 9), D(1, 2, 5).
39. A(2, -1, 7), B(6, 3, 1), C(3, 2, 8), D(2, -3, 7).
40. A(0, 4, 5), B(3, -2, 1), C(4, 5, 6), D(3, 3, 2).
41-50. Найти пределы, не пользуясь правилом Лопиталя.
41. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е) 
42. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
43. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
44. а)  ; б)
; б) 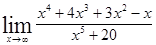 ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
45. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
46. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
47. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
48. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
49. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; e)
; e) 
50. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
51-60. Исследовать функцию на непрерывность в указанных точках.
51.  ; х1 = 1, х2 = 2.
; х1 = 1, х2 = 2.
52.  ; х1 = 2, х2 = 3.
; х1 = 2, х2 = 3.
53.  ; х1 = 2, х2 = 4.
; х1 = 2, х2 = 4.
54.  ; х1 = - 2, х2 = -1.
; х1 = - 2, х2 = -1.
55.  ; х1 = -3, х2 = -2.
; х1 = -3, х2 = -2.
56.  ; х1 = -3, х2 = -2.
; х1 = -3, х2 = -2.
57.  ; х1 = 2, х2 = 4.
; х1 = 2, х2 = 4.
58. 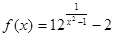 ; х1 = 1, х2 = 2.
; х1 = 1, х2 = 2.
59.  ; х1 = -5, х2 = -4.
; х1 = -5, х2 = -4.
60.  ; х1 = 4, х2 = 5.
; х1 = 4, х2 = 5.
61 - 70. Найти производные  данных функций.
данных функций.
61. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
62. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
63. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
64. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
65. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
66. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
67. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
68. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
69. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
70. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
51-60. Найти дифференциалы первого и второго порядка для заданных функций и вычислить их значения в заданной точке х0.
51.  , х0 = 0.
, х0 = 0.
52.  , х0 =1.
, х0 =1.
53.  , х0 = 0.
, х0 = 0.
54.  , х0 = 2.
, х0 = 2.
55.  , х0 =1.
, х0 =1.
56.  , х0 = 1.
, х0 = 1.
57.  , х0 = -1.
, х0 = -1.
58.  , х0 = 0.
, х0 = 0.
59.  , х0 = -1.
, х0 = -1.
60.  , х0 = 0.
, х0 = 0.
71-80. Найти пределы, используя правило Лопиталя.
71.  . 76.
. 76.  .
.
72.  . 77.
. 77.  .
.
73.  . 78.
. 78.  .
.
74.  . 79.
. 79.  .
.
75.  . 80.
. 80. 
81.-90. Исследовать методами дифференциального исчисления функции  и, используя результаты исследования, построить их графики.
и, используя результаты исследования, построить их графики.
81. а)  б)
б) 
82. а)  б)
б) 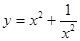
83. а)  б)
б) 
84. а)  б)
б) 
85. а)  б)
б) 
86. а)  б)
б) 
87. а)  б)
б) 
88. а)  б)
б) 
89. а)  б)
б) 
90. а)  б)
б) 
91-100. Найти экстремумы функции двух переменных  .
.
91.  . 9 6.
. 9 6.  .
.
92.  . 97.
. 97.  .
.
93.  . 9 8.
. 9 8. 
94.  . 99.
. 99.  .
.
95.  . 100.
. 100.  .
.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ.






