По Солоу произведенная продукция может быть использована только на потребление C (t), и на сбережения, инвестируемые в расширение производства I (t),т.е
Y(t) = C(t) + I(t). (4.6)
Доля доходов, идущая на инвестиции (норма сбережения) s – является постоянной. Тогда
Y(t) = C(t) + I(t) = C(t) + s Y(t). (4. 7)
С течением времени капитал изнашивается. Допустим, что норма амортизации (доля утраченного капитала за единичный интервал времени) 
также постоянна. Тогда валовые инвестиции за период времени dt будут равны сумме амортизационных расходов и чистого прироста капитала
. (4.8)
Поделив обе части (4.8) на dt, получим
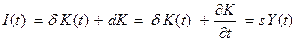. (4.9)
Допустим, что прирост трудовых ресурсов за единицу времени пропорционален имеющемуся объему этих ресурсов:
. (4.10)
Отсюда
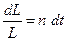(4.11)
Проинтегрируем это уравнение и получим:
. (4.12)
Константу C можно вычислить, если положить, что в начальный момент времени (t0 = 0), объем трудовых ресурсов составлял L 0.
Тогда:
,
.
откуда
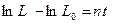
или 
(4.13)
Полученная закономерность соответствует модели Мальтуса, описывающей прирост населения (и пропорциональный ему рост объема трудовых ресурсов) в условиях отсутствия безработицы и неограниченного удовлетворения жизненных потребностей. Величина n называется темпом роста трудовых ресурсов.
Разделим (4.9) почленно на L. С учетом однородности производственной функции получим
. (4.14)
Величина η = K / L(4.15)
представляет собой капиталовооруженность – величина капитала, приходящаяся на одного работника. Приведенная функция
(4.16)
- это производительность труда, т.е. объем выпускаемой продукции в расчете на одного работника.
Рассмотрим скорость изменения капиталовооруженности.
С учетом правил дифференцирования можно записать:
. (4.17)
Но из (4.11) следует:
. (4.18)
Подставив (4.18) в (4.17). получаем
. (4.19)
Подставив в (4.19) вытекающее из (4.14) выражение
, (4.20)
получим уравнение накопления капитала:
. (4.21)
Рассмотрим статическое состояние системы, при котором капитал, приходящийся на одного работника, остается неизменным: η = η * = Сonst.
В этом случае производительность труда также постоянна:
σ* = f (η*) = Const.
Это означает, что запас капитала и выпуск продукции растут с тем же темпом, с которым растет население.
Из (4.21) следует, что стационарная величина капиталовооруженности может быть получена из выражения
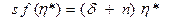. (4.21)
Это уравнение имеет графическое решение, показанное на рисунке 4.1
 | |||
 |
Рисунок 4.1- Графическое решение для статического состояния
Наклонная прямая показывает изменение объема инвестиций, необходимое для поддержания постоянной капиталовооруженности.
Кривая sf (η) показывает изменение размера сбережений на душу населения, а расстояние между производственной функцией f (η) и кривой сбережений sf ( η)– объем потребления на душу населения.
Точка пересечения кривой сбережений и наклонной прямой необходимых инвестиций определяет стационарный уровень капиталовооруженности η*.
Из анализа графика следует, что решение уравнения (4.21), а следовательно, и стационарное состояние системы, существует.
Из уравнения (4.21) следует, что при изменении нормы сбережения s должна измениться и стационарная капиталовооруженность η *. Это наглядно отображено и на рисунке 4.1.
Увеличение или уменьшение нормы сбережения s приводит к смещению кривой сбережений соответственно вверх или вниз.
При одном и том же положении прямой необходимых инвестиций точка пересечения кривой сбережений и прямой инвестиций в этих случаях смещается соответственно вправо или влево, что соответствует увеличению или уменьшению капиталовооруженности.
