Уравнение Шредингера позволяет найти пси-функцию данного состояния и, следовательно, определить вероятность нахождения частицы в различных точках пространства. Для этого надо:
- записать уравнение Шредингера с учетом конкретного вида потенциальной энергии;
- решить уравнение Шредингера, т.е. найти собственные функции и собственные значения, удовлетворяющие начальным и граничным условиям.
Пусть частица движется вдоль оси X. При этом движение ограничено отрезком (0 ,l). В точках x = 0 и x = l установлены непроницаемые бесконечно высокие стенки. Потенциальная энергия в этом случае имеет вид
Такая зависимость потенциальной энергии от x получила название потенциальной ямы.
Запишем стационарное уравнение Шредингера
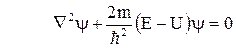
Поскольку пси-функция зависит только от координаты x, то уравнение упрощается следующим образом
Внутри потенциальной ямы U=0
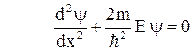
За пределы потенциальной ямы частица попасть не может. Поэтому вероятность обнаружения частицы вне ямы равна нулю. Соответственно и пси-функция за пределами ямы равна нулю. Из условия непрерывности следует, что ψ должна быть равна нулю и на границах ямы, т.е.
.
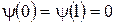Это граничное условие, которому должны удовлетворять решения уравнения.
Введем обозначение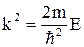 
и получим уравнение, хорошо известное из теории колебаний
Решение такого уравнения имеет вид гармонической функции
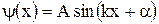
Выбор соответствующих параметров k и α определяется граничными условиями, а именно,
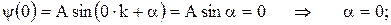
n = 0 отпадает, т.к. в этом случае ψ = 0 и частица нигде не находится. Следовательно, число k принимает лишь определенные дискретные значения, удовлетворяющие условию
.
Отсюда следует очень важный результат. Найдем собственные значения энергии частиц
,
т.е. энергия электрона в потенциальной яме не произвольна, а принимает дискретные значения, т.е. является квантованной. Величина Еn зависит от целого числа n, которое принимает значение от 1 до ∞ и носит название главного квантового числа. Квантованные значения энергии называются энергетическими уровнями, а квантовое число n определяет номер энергетического уровня. Таким образом, электрон в потенциальной яме может находиться на определенном энергетическом уровне En. Причем минимальное значение энергии, соответствующее первому энергетическому уровню, отлично от нуля
.
Определим расстояние между соседними энергетическими уровнями
При больших m и l расстояние между уровнями становится мало, и спектр становится квазинепрерывным. Относительное расстояние между уровнями
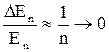при n → ∞,
т. е. спектр становится непрерывен. В этом заключается принцип соответствия Бора: при больших квантовых числах выводы и результаты квантовой механики должны соответствовать классическим результатам.
Вернемся к задаче определения собственных функций. После применения граничных условий имеем
Для нахождения коэффициента А воспользуемся условием нормировки
Значение интеграла равно l/2
Таким образом, собственные функции имеют вид
Графики собственных функций имеют вид
Окончательно сформулируем основные выводы:
1. Энергетический спектр частицы в потенциальной яме дискретный – энергия квантуется.
2. Минимальное значение кинетической энергии не может быть равно нулю.
3. Дискретный характер энергетических уровней проявляется при малых m,l и n, при больших m,l,n движение становится классическим.
4. Положения микрочастицы в яме не равновероятны, а определяются собственными функциями, в то время как в случае классической частицы все положения равновероятны.
