При течении реальной жидкости отдельные слои ее воздействуют друг на друга с силами, касательными к слоям. Это явление называют внутренним трением или вязкостью.
Рассмотрим течение вязкой жидкости между двумя твердыми пластинками (рис. 7.1), из которых нижняя неподвижна, а верхняя движется со скоростью uВ. Условно представим жидкость в виде нескольких слоев 1, 2, 3 и т. д. Слой, «прилипший» ко дну, неподвижен. По мере удаления от дна (нижняя пластинка) слои жидкости имеют все большие скорости (u1 < u2 < u3 <...), максимальная скорость uВ будет у слоя, который «прилип» к верхней пластинке.
Рис. 7.1
Слои воздействуют друг на друга. Так, например, третий слой стремится ускорить движение второго, носам испытывает торможение с его стороны, а ускоряется четвертым слоем и т. д. Сила внутреннего трения пропорциональна площади S взаимодействующих слоев и тем больше, чем больше их относительная скорость. Так как разделение на слои условно, то принято выражать силу в зависимости от изменения скорости на некотором участке в направлении х, перпендикулярном скорости, отнесенного к длине этого участка, т. е. от величины d u /dx — градиента скорости (скорости сдвига):
(7.1)
Это уравнение Ньютона. Здесь h — коэффициент пропорциональности, называемый коэффициентом внутреннего трения, или динамической вязкостью (или просто вязкостью). Вязкость зависит от состояния и молекулярных свойств жидкости (или газа).
Единицей вязкости является паскалъ-секунда (Па • с). В системе СГС вязкость выражают в пуазах (П): 1 Па • с = 10 П.
Для многих жидкостей вязкость не зависит от градиента скорости, такие жидкости подчиняются уравнению Ньютона (7.1), и их называют ньютоновскими. Жидкости, не подчиняющиеся уравнению (7.1), относят к неньютоновским. Иногда вязкость ньютоновских жидкостей называют нормальной, а неньютоновских — аномальной.
Жидкости, состоящие из сложных и крупных молекул, например растворы полимеров, и образующие благодаря сцеплению молекул или частиц пространственные структуры, являются неньютоновскими. Их вязкость при прочих равных условиях много больше, чем у простых жидкостей. Увеличение вязкости происходит потому, что при течении этих жидкостей работа внешней силы затрачивается не только на преодоление истинной, ньютоновской, вязкости, но и на разрушение структуры. Кровь является неньютоновской жидкостью.
7.2. Течение вязкой жидкости по трубам. Формула Пуазейля
Течение вязкой жидкости по трубам представляет для медицины особый интерес, так как кровеносная система состоит в основном из цилиндрических сосудов разного диаметра.
Вследствие симметрии ясно, что в трубе частицы текущей жидкости, равноудаленные от оси, имеют одинаковую скорость. Наибольшей скоростью обладают частицы, движущиеся вдоль оси трубы; примыкающий к трубе слой жидкости неподвижен.
Примерное распределение скорости слоев v жидкости в сечении трубы показано на рис. 7.2.
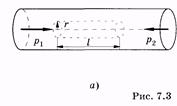
Для определения зависимости скорости слоев от их расстояния r от оси выделим мысленно цилиндрический объем жидкости некоторого радиуса r и длины l (рис. 7.3, а). На торцах этого цилиндра поддерживаются давления pl и р2 соответственно, что обусловливает результирующую силу
(7.2)
На боковую поверхность цилиндра со стороны окружающего слоя жидкости действует сила внутреннего трения, равная [см. (7.1)]
(7.3)
где S = 2p rl —площадь боковой поверхности цилиндра. Так как жидкость движется равномерно, то силы, действующие на выделенный цилиндр, уравновешены: F = F тр. Подставляя в это равенство (7.2) и (7.3), получаем
(7.4)
Знак «-» в правой части уравнения обусловлен тем, что du/d r < 0 (скорость уменьшается с увеличением r). Из (7.4) имеем
Проинтегрируем это уравнение:
(7.5)
здесь нижние пределы соответствуют слою, «прилипшему» к внутренней поверхности трубы (u= 0 при r = R), а верхние пределы — переменные. После интегрирования (7.5) получаем параболическую зависимость скорости слоев жидкости от расстояния их до оси трубы (см. огибающую концов векторов скорости на рис. 7.2):
Наибольшую скорость имеет слой, текущий вдоль оси трубы (r = 0):
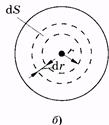
Установим, от каких факторов зависит объем Q жидкости, протекающей через горизонтальную трубу за 1 с. Для этого выделим цилиндрический слой радиусом r и толщиной d r. Площадь сечения этого слоя (рис. 7.3, б) dS = 2prdr. Так как слой тонкий, то можно считать, что он перемещается с одинаковой скоростью u. За 1 с слой переносит объем жидкости
d Q = ud S = u • 2prdr/. (7.7)
Подставляя (7.6) в (7.7), получаем
откуда интегрированием по всему сечению находим
Зависимость объема жидкости Q, протекающей через горизонтальную трубу радиуса R за 1 с, определяется формулой Пуазейля (7.8), где h — вязкость жидкости, а р1 - р2 — разность давлений, поддерживаемая на торцах трубы длиной l.
Как видно из (7.8), при заданных внешних условиях (р1 и р2) через трубу протекает тем больший объем жидкости, чем меньше ее вязкость и больше радиус трубы.
Проведем аналогию между формулой Пуазейля (7.8) и законом Ома для участка цепи без источника тока. Разность потенциалов соответствует разности давлений на концах трубы, сила тока — объему жидкости, протекающей через сечение трубы в 1 с, электрическое сопротивление — гидравлическому сопротивлению:
(7.9)
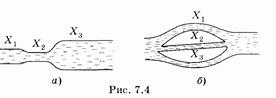Гидравлическое сопротивление тем больше, чем больше вязкость h, длина l трубы и меньше площадь поперечного сечения. Аналогия между электрическим и гидравлическим сопротивлениями позволяет в некоторых случаях использовать правило нахождения электрического сопротивления последовательного и параллельного соединений проводников для определения гидравлического сопротивления системы последовательно или параллельно соединенных труб. Так, например, общее гидравлическое сопротивление трех труб, соединенных последовательно (рис. 7.4, а) и параллельно (рис. 7.4, б), вычисляется соответственно по формулам:
Х = Х1 + Хг + Х3, (7.10)
(7.11)
Чтобы придать уравнению Пуазейля более общее выражение, справедливое и для труб переменного сечения, заменим (р 1 - р2)/dl градиентом давления dp/dl, и тогда
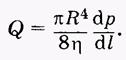(7.12)
Установим в разных местах горизонтальной цилиндрической трубы разного сечения, по которой течет вязкая жидкость, манометрические трубки (рис. 7.5, а). Они показывают, что статическое давление вдоль трубы переменного сечения убывает пропорционально l: dp/dl = const. Так как величина Q одинакова (несжимаемая жидкость), то [см. (7.12)] градиент давления больше в трубах меньшего радиуса. График зависимости давления от расстояния вдоль труб разного радиуса приближенно показан на рис. 7.5, б
|
Физические вопросы гемодинамики
Гемодинамикой называют область биомеханики, в которой исследуется движение крови по сосудистой системе. Физической основой гемодинамики является гидродинамика Течение крови зависит как от свойств крови, так и от свойств кровеносных сосудов
В главе рассматриваются также физические основы работы некоторых технических устройств, используемых в связи с кровообращением.
