Пусть функция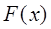 
и функции 
имеют непрерывные частные производные в некоторой окрестности точки 
и пусть эта точка является точкой локального минимума функции 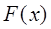при ограничениях . Тогда существуют такие неотрицательные множители Лагранжа 
, что для функции Лагранжа 
точка является стационарной точкой функции, т.е.
(21)
Поясним смысл теоремы на примерах.
| Пример1 Иллюстрация к условиям существования минимума в задаче оптимизации с ограничениями неравенствами. |
Аналогия: мяч катится по долине, ограниченной заборами (ограничения неравенства, 
) и останавливается в точке 
(на активном ограничении 
) с минимальным значением функции 
.
Эта точка характеризуется балансом сил 
, 
.
| Пример2
Рассмотрим двумерную задачу нелинейного программирования, в которой область допустимых значений  задается тремя ограничивающими функциями.
|
Если точка находится внутри множества (т.е. является стационарной точкой функции 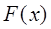, то теорема будет справедлива, если положить все множители Лагранжа 
равными нулю.
Пусть теперь точка 
находится на одной из дуг, например, на дуге AB, т.е. пусть ограничение 
является активным ограничением, а остальные ограничения – неактивными ограничениями. Тогда 
и справедливость теоремы вытекает из правила множителей Лагранжа для задачи с ограничениями типа равенств, если положить 
.
Пусть, наконец, точка находится в одной из угловых точек множества 
, например, в точке 
, т.е. пусть ограничения 
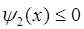являются активными ограничениями, а ограничение 
– неактивным ограничением. Тогда можно положить 
и справедливость теоремы вытекает из правила множителей Лагранжа для задачи с ограничениями типа равенств.
Теорема означает, что в ее условиях вместо задачи условной оптимизации (18), (19) можно решать задачу безусловной оптимизации
(22)
Следствие из теоремы. Существуют такие неотрицательные множители Лагранжа , что имеют место следующие равенства:
· Условие стационарности по 
: 
(23)
· Условие допустимости решения 
(24)
(для максимума 
)
Кроме того, выполняется условие дополняющей нежесткости
(25)
Из этого условия следует, что если ограничение в точке неактивное, т.е. 
, то 
, а если активное, т.е. 
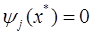, то 
(для минимума) и 
(для максимума).
Из (21) следует, что антиградиент целевой функции является неотрицательной (неположительной в случае максимума) линейной комбинацией градиентов функций, образующих активные ограничения в точке .
(26)
где индекс 
означает активное ограничение.
| На рисунке в точке С достигается минимум и выполняется условие равенство (26), а в точке А нет. |
