Достаточными условиями глобального минимума задачи (1) является выпуклость критерия (1) и выпуклость допустимой области ограничений (2), (3).
Допустимое множество 
называется выпуклым, если для любых точек 
и для любого 
выполняется соотношение 
.
Выпуклое множество Не выпуклое множество
Примеры выпуклых множеств в пространстве 
:
o все евклидово пространство;
o любой отрезок 
;
o гиперплоскость 
;
o полупространство 
;
o симплекс,
o гиперпараллелепипед,
o выпуклый многогранник,
o гипершар;
o пересечение любого конечного числа выпуклых множеств.
Выпуклый критерий оптимальности
Непрерывный критерий оптимальности 
, где и множество является выпуклым множеством, называется выпуклым [строго выпуклым] критерием оптимальности, если для любых 
и любого 
выполняется неравенство (4) [(5)].
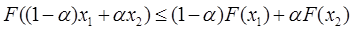(4)
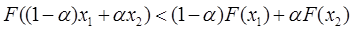(5)
где произвольное число
Аналогично, с заменой знака неравенства на противоположный, можно определить вогнутый и строго вогнутый критерийоптимальности.
Геометрический смысл выпуклости: все точки кривой на интервале 
лежат под соответствующей хордой.
Строго выпуклый критерий является унимодальным критерием.
Условия существования минимума в безусловных задачах оптимизации
Одномерная задача оптимизации
Рассмотрим задачу 
Необходимое условие минимума
(6)
Решениями уравнения (6) являются стационарные точки – минимума, максимума и перегиба функции .
На рисунке 
, 
– точки локальных минимумов; 
– точка локального максимума; 
– точка перегиба функции .
Необходимые и достаточные условия минимума дважды непрерывно дифференцируемой функции , определенной на интервале 
:
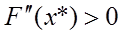
Многомерная задача безусловной оптимизации
|
Представление минимизируемой
функции в виде линий равного
уровня (контуры F(x1,x2)).
|
Условия существования минимума в задаче оптимизации без ограничений
(7)
Необходимое условие минимума 
:
(8)
где 
– градиент 
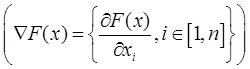в точке 
.
Решениями уравнения (8) являются стационарные точки.
Необходимое и достаточное условие минимума дважды непрерывно дифференцируемой функции в окрестности точки 
:
(9)
где 
– 
-матрица Гессе (вторых производных) функции
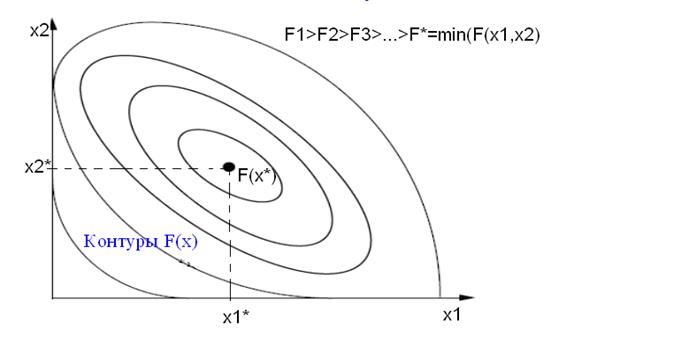Иллюстрация к условиям существования минимума в задаче оптимизации без ограничений
Условия существования минимума в условных задачах оптимизации
Задача условной оптимизации с ограничениями типа равенств Функция Лагранжа
Рассмотрим задачу: 
(10)
где 
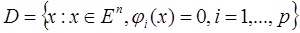(11)
Функция Лагранжа для задачи (10) с ограничениями (11) определяется формулой
(12)
где 
, – вектор множителей Лагранжа, размерности 
.
