Материальная система – совокупность материальных точек, движение которых взаимосвязаны. Масса системы = сумме масс всех точек (или тел), образующих систему: М=åmk. Центр масс (центр инерции) – геометрическая точка, радиус-вектор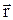 
которой определяется равенством: 
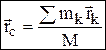, где 
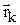– радиусы-векторы точек, образующих систему. Координаты центра масс: 
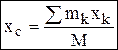и т.д. Внешние силы Fe – силы, действующие на точки системы со стороны тел, не входящих в систему. Внутренние силы Fi – силы, вызванные взаимодействием точек, входящих в систему. Свойства внутренних сил: 1) Геометрическая сумма (главный вектор) всех внутренних сил = 0; 2) Геометрическая сумма моментов всех внутренних сил относительно произвольной точки = 0. Дифф-ные ур-ния движения системы матер.точек:
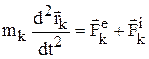или в проекциях на оси координат: 
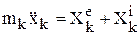и т.д. для каждой точки (тела) системы. Геометрия масс.
Момент инерции матер.точки относительно некоторой оси называется произведение массы m этой точки на квадрат ее расстояния h до оси: mh2. Момент инерции тела (системы) относительно оси Оz: Jz= åmkhk2. При непрерывном распределении масс (тело) сумма переходит в интеграл: Jx= ò(y2+z2)dm; Jy= ò(z2+x2)dm; Jz= ò(x2+y2)dm – относительно координатных осей. Jz= M×r2, r – радиус инерции тела – расстояние от оси до точки в которой нужно сосредоточить всего тела, чтобы ее момент инерции равнялся моменту инерции тела. Момент инерции относительно оси (осевой момент инерции) всегда >0. Полярный момент инерции Jo= ò(x2+y2+z2)dm; Jx+Jy+Jz= 2Jo. Центробежный момент инерции Jxy для матер.точки называется произведение ее координат x и y на ее массу m. Для тела центробежными моментами инерции называются величины, определяемые равенствами: Jxy=òxy dm; Jyz=òyz dm; Jzx=òzx dm. Центробежные моменты инерции симметричны относительно своих индексов, т.е. Jxy=Jyx и т.д. В отличие от осевых, центробежные моменты инерции могут иметь любой знак и обращаться в нуль. Главной осью инерции тела назыв. ось, для которой оба центробежных момента инерции, содержащие индекс этой оси, равны нулю. Например, если Jxz=Jyz=0, то ось z – главная ось инерции. Главной центральной осью инерции назыв. главная ось инерции, проходящая через центр масс тела. 1)Если тело имеет плоскость симметрии, то любая ось, перпендикулярная к этой плоскости, будет главной осью инерции тела для точки, в которой ось пересекает плоскость. 2)Если тело имеет ось симметрии, то эта ось является главной осью инерции тела (ось динамической симметрии). Размерность всех моментов инерции [кгм2]
Центробежный момент инерции зависят не только от направления координатных осей, но и от выбора начала координат.
Тензор инерции в данной точке: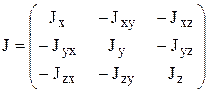 
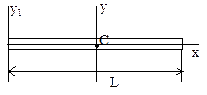Моменты инерции некоторых однородных тел:
стержень массы m и длины L: 
; 
.
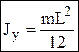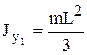Однородный сплошной диск с центром в точке С радиуса R и массы m: 
. Полый цилиндр: 
,
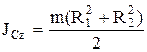цилиндр с массой распределенной по ободу (обруч):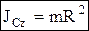 
.
Теорема Гюйгенса-Штейнера момент инерции тела относительно произвольной оси равен моменту инерции относительно оси ей параллельной и проходящей через центр масс тела плюс произведение массы тела на квадрат расстояния между осями:
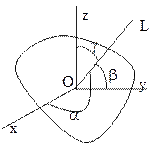
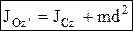
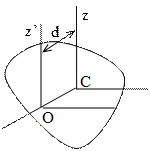. Наименьший момент инерции будет относительно той оси, которая проходит через центр масс. Момент инерции относительно произвольной оси L: J = Jxcos2a + Jycos2b + Jzcos2g – 2Jxycosacosb – 2Jyzcosbcosg – 2Jzxcosgcosa,
если координатные оси являются главными относительно своего начала, то:
J = Jxcos2a + Jycos2b + Jzcos2g. Теорема о движении центра масс системы.
Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил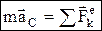 
– дифференциальное уравнение движения центра масс. В проекциях на оси координат: 
.
Закон сохранения движения центра масс. Если главный вектор (векторная сумма) внешних сил остается все время равным нулю, то центр масс механической системы находится в покое или движется прямолинейно и равномерно. Аналогично в проекциях на оси, если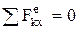 
Þ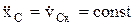 
, если при этом в начальный момент vCx0= 0, то Þ 
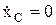Þ xC= const.
Количество движения системы Q (иногда обозначают К) – вектор, равный геометрической сумме (главному вектору) количеств движения всех точек системы:
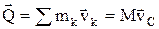, М – масса всей системы, vC – скорость центра масс.
Теорема об изменении количества движения системы: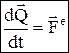 
– производная по времени от количества движения механической системы геометрически равна главному вектору внешних сил, действующих на эту систему. В проекциях: 
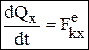, и т.д. Теорема об изменении кол-ва движения системы в интегральной форме:
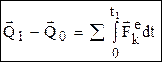, где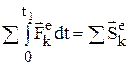 
– импульсы внешних сил.
В проекциях: Q1x – Q0x = åSekx и т.д. количество движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени. Закон сохранения количества движения – если сумма всех внешних сил, действующих на систему, = 0, то вектор количества движения системы будет постоянен по модулю и направлению: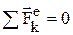 
Þ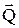 
= const, аналогично в проекциях: 
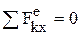Þ Qx= const. Из закона следует, что внутренние силы изменить суммарное количество движение системы не могут. Тело переменной массы, масса которого непрерывно изменяется с течением времени m= f(t) (пр.: ракета, топливо которой убывает). Дифф-ное уравнение движения точки переменной массы:
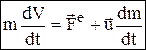– уравнение Мещерского, u – относительная скорость отделяющихся частиц. 
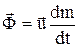– реактивная сила, 
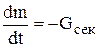— секундный расход топлива, 
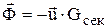. Реактивная сила направлена в противоположную сторону относительной скорости истечения топлива.
Формула Циолковского: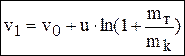 
— определяет скорость ракеты, когда все топливо будет израсходовано – скорость в конце активного участка, mт– масса топлива, mk– масса корпуса ракеты, v0 – начальная скорость. 
– число Циолковского, m0 – стартовая масса ракеты. От режима работы ракетного двигателя, т.е. от того насколько быстро сжигается топливо, скорость ракеты в конце периода горения не зависит. Для достижения 1-ой космической скорости 7,9 км/с, при m0/mk= 4, скорость отброса должна быть 6 км/с, что трудно осуществить, поэтому применяются составные (многоступенчатые) ракеты.
Главный момент количеств движения матер. системы (кинетический момент)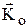 
– величина, равная геометрической сумме моментов количеств движения всех точек системы относительно центра О. 
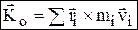. Теорема об изменении момента количеств движения системы (теорема об изменении кинетического момента):
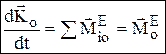— производная по времени от кинетического момента механич. системы относительно некоторого неподвижного центра геометрически равна главному моменту внешних сил, действующих на эту систему относительно того же центра. Аналогичные равенства относительно осей координат: 
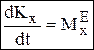и т.д.
Закон сохранения кинетического момента: если 
, то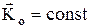 
. Главный момент количеств движения системы является характеристикой вращательного движения. Кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость тела: Kz = Jzw. Если Mz= 0, то Jzw = const, Jz – момент инерции тела..
Кинетическая энергия системы – скалярная величина Т, равная арифметической сумме кинетической энергий всех точек системы: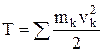 
. Если система состоит из нескольких тел, то Т = åТк. Поступательное движение: Тпост= 
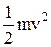. Вращательное движ-ие: Твр= 
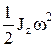, Jz– момент инерции относительно оси вращения. Плоскопараллельное (плоское) движ-ие: Тпл= 
+ 
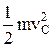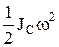, vC – скорость центра масс. Общий случай: Т= + 
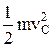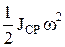, JCP – момент инерции тела относительно мгновенной оси. Теорема Кенига: Т= + 
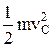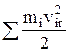– кинетич. энергия мех. сист. = сумме кинетич. энергии центра масс системы, масса которого равна массе всей системы, и кинетич. энергии этой системы в ее относительном движении относительно центра масс. Работа силы: 
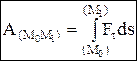, работа момента: 
. Мощность: N= Fv, N=Mzw. Теорема об изменении кинетической энергии системы: в дифференциальной форме: dT =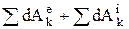 
, 
, 
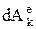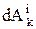– элементарные работы, действующих на точку внешних и внутренних сил, в конечной форме:
Т2 – Т1=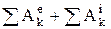 
. Для неизменяемой системы 
и Т2 – Т1=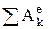 
, т.е. изменение кинетической энергии твердого тела на некотором перемещении равно сумме работ внешних сил, действующих на тело на этом перемещении. Если сумма работ реакций связей на любом возможном перемещении системы равна нулю, то такие связи называются идеальными. Коэффициент полезного действия (кпд): 
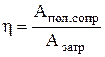< 1, Апол.сопр. – работа полезных сил сопротивления (сил, для которых предназначена машина), Азатр= Апол.сопр.+ Авр.сопр. – затраченная работа, Авр.сопр.-– работа вредных сил сопротивления (силы трения, сопротивления воздуха и т.п.).
h= Nмаш/Nдв, Nмаш – полезная мощность машины, Nдв – мощность дв-ля, приводящего ее в движение. Закон сохранения полной механической энергии: Т + П = const. Если система движется под действием потенциальных сил, то сумма кинетической и потенциальной энергий сохраняет постоянное значение. (Т + П — интеграл энергии). Потенциальные силы – силы, работа которых не зависит от вида траектории, по которой перемещается точка (пр.: сила тяжести, сила упругости) Непотенциальные – напр.: силы трения. Механическая энергия – сумма кинетической и потенциальной энергий. Расход механической энергии обычно означает превращение ее в теплоту, электричество, звук или свет, а приток механической энергии связан с обратным процессом превращения различных видов энергии в механическую энергию.
Динамика твердого тела
Дифференциальные ур-ния поступательного движения твердого тела: 
и т.д.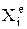 
– проекция внешней силы. Все точки тела движутся так же, как и его центр масс С. Для осуществления поступательного движения необходимо, чтобы главный момент всех внешних сил относительно центра масс был равен 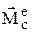0: 
=0.
Дифф-ные ур-ния вращения твердого тела вокруг неподвижной оси: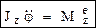 
,
Jz – момент инерции тела относительно оси вращения z,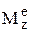 
– момент внешних сил относительно оси вращения (вращающий момент). 
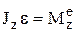, e – угловое ускорение, чем больше момент инерции при данном 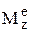, тем меньше ускорение, т.е момент инерции при вращательном движении является аналогом массы при поступательном. Зная 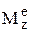, можно найти закон вращения тела j=f(t), и, наоборот, зная j=f(t), можно найти момент. Частные случаи: 1) если 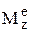= 0, то w = const – тело вращается равномерно; 2) 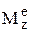= const, то e = const – вращение равнопеременное. Уравнение аналогичное дифф-ному уравнению прямолинейного движения точки 
.
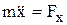Физический маятник – твердое тело, совершающее колебания вокруг неподвижной горизонтальной оси под действием силы тяжести. Ур-ние вращательного движения:
, обозначая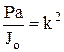 
, получаем дифф-ное уравнение колебаний маятника: 
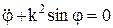, k – частота колебаний маятника. Рассматривая малые колебания, можно считать sinj» j, тогда 
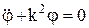– дифф-ное уравнение гармонических колебаний. Решение этого уравнения: j = С1coskt + C2 sinkt или j = asin(kt + b), a – амплитуда колебаний маятника, b – начальная фаза колебаний. Период малых колебаний физического маятника Т= 2p/k = 2p 
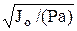. Для малых колебаний маятника период не зависит от угла начального отклонения, этот результат является приближенным. Для математического маятника (материальной точки, подвешенной на нерастяжимой нити и движущейся под действием силы тяжести) имеем дифф. уравнения движения:
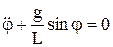, L – длина нити. Если L= 
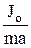, то математический маятник будет двигаться так же, как и физический (период колебаний совпадает). Величина L назыв-ся приведенной длиной физического маятника. Точка К, отстоящая от оси подвеса на расстоянии ОК=L, назыв-ся центром качаний физич. маятника. Если ось подвеса взять в точке К, то точка О будет центром качаний и наоборот – свойство взаимности. Расстояние ОК всегда >ОС, т.е. центр качаний всегда расположен ниже центра масс.
