Любая финансовая, кредитная или коммерческая операция предполагает совокупность условий, согласованных её участниками. К таким условиям относятся: сумма кредита, займа или инвестиций, цена товара, сроки, способы начисления процентов и погашения долга и т.д. Совместное влияние на финансовую операцию многих факторов делает её конечный результат неочевидным. Для его оценивания необходим специальный количественный анализ. Совокупность методов этого анализа составляет предмет финансовой математики.
В данном разделе рассмотрим финансовые вычисления, необходимые для анализа сделок, включающих три основных элемента − размер платежа, срок и ставку процентов. Эти условия обязательно оговариваются сторонами при заключении любых внутренних и внешних финансово-экономических сделок. Так что, обе стороны заинтересованы в объективной и грамотной количественной оценке условий сделки, которая производится на основе финансовых вычислений.
К основным понятиям, которыми оперируют в финансовых вычислениях, относятся: размер займа или кредита, процент, ставка процента, период начисления, учетная ставка, методы наращения и дисконтирования платежей, и т.д.
В практических финансово-экономических расчетах суммы денег обязательно связывают с некоторыми моментами или интервалами времени. Для этого в договорах фиксируются соответствующие сроки, даты и периодичность поступлений денежных средств, а также их выплат.
Необходимость учета фактора времени определяется принципом неравнозначности денег, относящихся к разным моментам времени. Даже в условиях отсутствия инфляции и риска одна и та же сумма денег сегодня и полученная через год неравноценны. Теоретически это обусловлено тем, что любая сумма денег может быть инвестирована и принести доход. Поступившие доходы в свою очередь могут быть реинвестированы, и т.д. Поэтому сегодняшние деньги в этом смысле ценнее будущих. В финансовых вычислениях учет фактора времени осуществляется с помощью начисления процентов.
Под процентными деньгами или процентами в финансовых расчетах понимают абсолютную величину дохода от предоставления денег в долг в любой форме: выдача денежной ссуды, продажа в кредит, помещение денег на сберегательный счет и т.д.
Размер процентной ставки − отношение суммы процентных денег, выплачиваемых за фиксированный отрезок времени, к величине ссуды. Интервал времени, к которому относится процентная ставка, называются периодом начисления. Начисление процентов, как правило, производится дискретно, т.е. в отдельные моменты времени, причем в качестве периодов начисления принимают год, полугодие, квартал, месяц.
Проценты либо выплачиваются кредитору по мере их начисления, либо присоединяются к сумме долга. Процесс увеличения денег в связи с присоединением процентов к сумме долга называют наращением, или капитализацией.
В практике существуют различные способы начисления процентов, зависящие от условий контрактов. Соответственно применяют различные виды процентных ставок. Одно из основных отличий связано с выбором исходной суммы для начисления процентов. Ставки процентов могут применяться к одной и той же начальной сумме на протяжении всего срока ссуды или к сумме с начисленными в предыдущем периоде процентами. В первом случае они называются простыми, а во втором − сложными процентными ставками. Процентные ставки могут быть постоянными или переменными. В этом случае значение ставки равно сумме некоторой изменяющейся во времени базовой величины и надбавки к ней, которую называют маржой. Размер маржи определяется рядом условий, например сроком операции, и обычно он находится в пределах 0,5−5%. В контракте может использоваться и переменный во времени размер маржи.
Рассмотрим методы анализа сделок, в которых предусматриваются разовые платежи при выдаче и погашении кредита или депозита. Задачи такого анализа сводятся к расчету наращенной суммы, суммы процентов и размера дисконта.
Формула наращения по простым процентам
Под наращенной суммой ссуды (долга, депозита и т.д.) понимается её первоначальная сумма вместе с начисленными на неё процентами к концу срока.
Пусть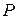 
– первоначальная сумма денег, 
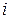− ставка простых процентов. Начисленные проценты за один период равны 
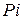, за 
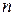периодов − 
.
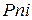Процесс изменения суммы долга с начисленными простыми процентами можно представить в виде арифметической прогрессии, членами которой являются величины
, 
, 
,..., 
.
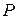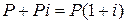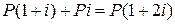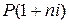Первый член этой прогрессии равен 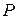, разность − 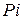, тогда последний член (
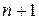)-ый является наращенной суммой:
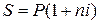. (1)
Формула (1) является формулой наращения по простым процентам, или формулой простых процентов. Множитель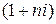 
называется множителем наращения. Он показывает, во сколько раз наращенная сумма больше первоначальной суммы.
Наращенную сумму можно представить в виде двух слагаемых: первоначальной суммы 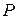и суммы процентов 
:
,
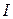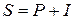где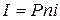 
.
Начисление простых процентов обычно используется в двух случаях: а) при заключении краткосрочных контрактов (представление краткосрочных кредитов и т.п.), срок которых не превышает года; б) когда проценты не присоединяются к сумме долга, а выплачиваются периодически.
Ставка процентов устанавливается в расчете за год, поэтому при продолжительности ссуды менее года необходимо выяснить, какая часть процента уплачивается кредитору. Для этого величину 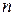выражают в виде дроби
,
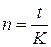где 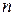− срок, в долях года; 
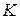− число дней в году (временная база); 
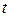− срок операции.
В зависимости от того, какое количество дней в году берется за базу 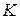, различают два вида процентов:
· обыкновенный процент (коммерческий), когда в году принимается 360 дней, т.е. 12 месяцев по 30 дней;
· точный процент получают, когда за базу берут действительное число дней в году: 365 или 366.
В зависимости от числа дней пользования ссудой 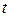различают два способа начисления процентов:
· точный способ − вычисляется фактическое число дней между двумя датами;
· приближенный способ − продолжительность ссуды определяется числом месяцев и дней ссуды, когда все месяцы содержат по 30 дней.
Следует помнить, что в обоих случаях дата выдачи и дата погашения долга считается за один день.
С учетом этого, на практике могут применяться три варианта расчета процентов:
а) точные проценты с точным числом дней ссуды (английская практика);
б) обыкновенные проценты с точным числом дней ссуды (французская практика);
в) обыкновенные проценты с приближенным числом дней ссуды (германская практика).
Сложные проценты
Сложные проценты применяются в долгосрочных финансово-кредитных операциях, если проценты не выплачиваются периодически сразу после их начисления за прошедший интервал времени, а присоединяются к сумме долга. Присоединение начисленных процентов к сумме, которая служила базой для их определения, называют капитализацией процентов.
Пусть первоначальная сумма долга равна 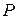, тогда через один год сумма долга с присоединенными процентами составит 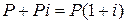, через два года − 
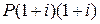, через 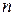лет −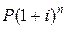 
. Таким образом, получаем формулу наращения для сложных процентов
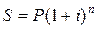, (2)
где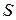 
− наращенная сумма, 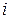− годовая ставка сложных процентов; 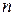− срок ссуды; 
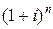− множитель наращения.
В практических расчетах в большинстве случаях применяют дискретные проценты, т.е. проценты, начисляемые за одинаковые интервалы времени (год, полугодие, квартал и т.д.).
Наращение по сложным процентам представляет собой рост по закону геометрической прогрессии, первый член которой равен 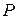, а знаменатель 
.
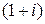Наращенные суммы по формулам простых и сложных процентов (множители наращения, соответственно,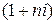 
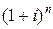и различаются между собой даже при условии одинакового периода начисления и одинаковой процентной ставки.
Аннуитетные и дифференцированные платежи
Часто в контрактах финансового характера предусматривают не отдельные разовые платежи, а серию платежей, распределенных во времени. Например, регулярные выплаты с целью погашения долгосрочного кредита вместе с начисленными на него процентами. Очевидно что, заемщики хотят взять кредит на выгодных условиях, под которыми следует понимать максимально низкую процентную ставку и минимальную итоговую переплату.
Различают аннуитетные и дифференцированный платежи.
Дифференцированные платежи представляют собой непостоянную сумму, состоящую из фиксированной части (получается путем деления суммы кредита на количество месяцев кредитования) и процентов, начисленных на остаток долга по займу.
Формула дифференцированного платежа следующая
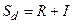, (3)
где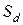 
− дифференцированный платеж; 
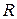− ежемесячное погашение кредита: 
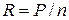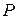( − сумма кредита, 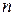− число периодов погашения кредита); 
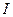− проценты, начисленные на остаток долга за период.
Дифференцированные платежи характерны тем, что задолженность по кредиту погашается равномерно, начиная с самых первых выплат, а проценты начисляют по фактическому остатку. Таким образом, каждый последующий платеж меньше предыдущего. Досрочное погашение не ограничено ни по времени, ни по сумме и позволяет существенно сэкономить на выплачиваемых процентах.
Аннуитет − начисление равных платежей на весь срок погашения кредита. Сумма аннуитетного платежа состоит из суммы основного долга, а также процентов, начисленных на остаток долга по кредиту.
Формула аннуитетного платежа:
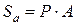, (4)
где 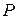− сумма кредита; 
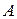− коэффициент аннуитета:
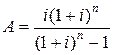. (5)
Здесь 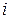− процентная ставка, выраженная в сотых долях в расчете на период (например, для случая 12% годовых и ежемесячного платежа это составит 
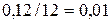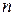); − число периодов погашения кредита.
При аннуитетном способе в первой половине срока погашения задолженность по кредиту практически не гасится, а выплачиваются, в большей части, проценты. Эта особенность делает платежи относительно небольшими, но значительно увеличивают общую сумму начисляемых процентов.
Пример расчета погашения кредита при разных методах начисления платежей: аннуитетного и дифференцированного приведен в файле ПРИМЕР_ЗАДАНИЕ_1.exlx.
