Высшая математика: Методические рекомендации по выполнению домашней контрольной работы №1 / Е.А. Сбродова, М.А. Сагадеева. – Челябинск: ОУ ВО «Южно-Уральский институт управления и экономики», 2015.– 33 с.
Высшая математика: Методические рекомендации по выполнению домашней контрольной работы № 1: 08.03.01 «Строительство»
ã Издательство ОУ ВО «Южно-Уральский институт управления и экономики», 2015
СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 4
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ.. 5
ЗАДАНИЯ ДЛЯ ДОМАШНИХ КОНТРОЛЬНЫХ РАБОТ. 21
РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ.. 31
ВВЕДЕНИЕ
Целью преподавания дисциплины «Высшая математика» состоит в ознакомлении студентов данного направления с основными понятиями, положениями и методами математики. Дисциплина «Высшая математика» формирует базовые знания и кругозор, необходимые для освоения обще-профессиональных и специальных дисциплин. Данный курс способствует созданию условий для формирования профессиональных навыков будущего специалиста.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ
Раздел 1 Элементы линейной и векторной алгебры
Тема 1.1 Матрицы и определители
Алгебраическая операция и ее свойства. Определение и примеры группы, кольца, поля. Определение матрицы. Виды матриц. Транспонирование матриц. Алгебраические операции над матрицами. Свойства алгебраических операций над матрицами. Определители второго, третьего порядков и матрицы n-го порядка. Свойства определителей. Алгебраические дополнения и их свойства. Присоединенная и обратная матрицы. Критерий обратимости. Метод Жордана-Гаусса нахождения обратной матрицы. Ранг матрицы как наивысший порядок ее миноров, отличных от нуля. Вычисление ранга матрицы с помощью элементарных преобразований. Линейная комбинация, линейная зависимость и независимость строк (столбцов) матрицы. (1, гл.1, §1.1-1.6; с.9-35); (2, гл.1).
Матрица – это прямоугольная таблица, составленная из m·n чисел, расположенных в m строках и n столбцах. Обращение к элементу матрицы происходит указанием номера строки и номера столбца. Например, элемент a27 (читается: а два семь) стоит во второй строке и седьмом столбце. Следует изучить основные алгебраические операции, выполняемые над матрицами: умножение матрицы на число, сложение, умножение матриц, транспонирование, и их свойства.
Относительные трудности возникают при усвоении операции умножения матриц. Необходимо твердо усвоить формальное правило умножения (1, с. 12–13) и связанное с ним условие существования произведения АВ матриц А и В:число столбцов матрицы А должно быть равно числу строк матрицы В. Одна из особенностей операции умножения состоит в том, что произведение матриц в общем случае не коммутативно, т.е. АВ ¹ ВА. Если матрицы А и В не квадратные, то это свойство очевидно, так как либо одно из произведений АВ или ВА не существует, либо АВ и ВА – матрицы разных размеров. Даже если А и В – квадратные матрицы, в общем случае АВ ¹ ВА, в чем нетрудно убедиться на любом частном примере. Другая особенность произведения матриц состоит в том, что произведение двух ненулевых матриц может оказаться нулевой матрицей.
Например, можно легко показать, что произведение матриц есть нулевая матрица (сравните: во множестве действительных чисел произведение равно нулю тогда, когда хотя бы один из сомножителей равен нулю).

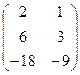 =
= 
При изучении понятия определителей необходимо уяснить, что определитель есть число, сопоставляемое квадратной матрице по определенным правилам. Однако, эти правила не дают эффективного способа вычисления определителей. Легко запоминаются лишь формулы для вычисления определителей второго и третьего порядков (это необходимо сделать!) (1, пример 1.9, c.25, 26).. Основные свойства определителей помогут решить задачу вычисления определителей более высокого порядка. Попробуйте с этим разобраться.
Важным определением в теории матриц является определение обратной матрицы. Оказывается, обратная матрица существует не всегда (!), а лишь в тех случаях, когда ее определитель отличен от нуля. Для того, чтобы вычислить обратную матрицу нужно знать определение присоединенной матрицы, уметь их вычислять, Проверить правильность вычисления обратной матрицы довольно просто. Для этого вычислите произведение АА-1 или А-1 А. Если в результате Вы получите единичную матрицу, то обратная матрица А-1 найдена правильно.
Для усвоения материала необходимо разобрать задачи (1, 1.15 – 1.29).
Пример: Найти матрицу С=ВT×АT×А×В, если А=  , В=
, В=  .
.
Решение:
Алгоритм решения:
1. Находим матрицы ВT, АT, транспонированные к матрицам А и В.
АT=  , ВT=
, ВT=  .
.
2. Находим произведение матриц:
ВT×АT=  ×
×  =
=  .
.
3. Находим произведение матриц:
А×В= 
 =
=  .
.
4. Находим произведение
С=ВT×АT×А×В= 
 =
=  .
.
Ответ: C=  .
.






