Синтаксис команд.
Стандартная команда Maple состоит из имени команды и ее параметров, указанных в круглых скобках: command(p1, p2, …). В конце каждой команды должен быть знак (;) или (:). Разделитель (;) означает, что в области вывода после выполнения этой команды будет сразу виден результат. Разделитель (:) используется для отмены вывода, то есть когда команда выполняется, но ее результат на экран не выводится.
Символ процента (%) служит для вызова предыдущей команды. Этот символ играет роль краткосрочной замены предыдущей команды с целью сокращения записи. Пример использования (%):
> a+b;
a+b
> %+c;
a+b+c.
Для присвоения переменной заданного значения используется знак присвоить (:=).
Когда программа Maple запускается, она не имеет ни одной команды, полностью загруженной в память. Большая часть команд имеют указатели их нахождения, и при вызове они загружаются автоматически. Другие команды находятся в стандартной библиотеке и перед выполнением обязательно должны быть вызваны командой readlib(command), где command – имя вызываемой команды. Остальная часть процедур Maple содержится в специальных библиотеках подпрограмм, называемых пакетами. Пакеты необходимо подгружать при каждом запуске файла с командами из этих библиотек. Имеется два способа вызова команды из пакета:
1. можно загрузить весь пакет командой with(package) где package – имя пакета;
2. вызов какой-нибудь одной команды command из любого пакета package можно осуществить, если набрать команду в специальном формате:
> package[command](options);
где вначале записывается название пакета package, из которого надо вызвать команду, а затем в квадратных скобках набирается имя самой команды command, и после чего в круглых скобках следуют параметры options данной команды.
К библиотекам подпрограмм Maple относятся, например, следующие пакеты: linalg – содержит операции линейной алгебры; geometry – решение задач планиметрии; geom3d – решение задач стереометрии; student – содержит команды, позволяющие провести поэтапное решение задачи в аналитическом виде с промежуточными вычислениями.
Стандартные функции.
| Стандартные функции Maple | |
| Математическая запись | Запись в Maple |
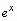
| exp(x) |
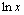
| ln(x) |
| log10(x) |
| log[a](x) |
| sqrt(x) |
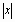
| abs(x) |
| sin(x) |
| cos(x) |
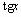
| tan(x) |
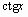
| cot(x) |
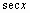
| sec(x) |
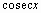
| csc(x) |
| arcsin(x) |
| arccos(x) |
| arctan(x) |
| arccot(x) |
| sinh(x) |
| cosh(x) |
| tanh(x) |
| coth(x) |
 - функция Дирака
| Dirac(x) |
 - функция Хевиссайда
| Нeaviside(х) |
Maple содержит огромное количество специальных функций, таких, как Бесселевы функции, Эйлеровы бета- и гамма – функции, интеграл ошибок, эллиптические интегралы, различные ортогональные полиномы.
С помощью функции exp(x) определяется число е =2.718281828… посредством записи exp(1).
Задание 3.
1. Перейдите в текстовый режим и наберите “Задание №3”. После не забудьте перейти в режим командной строки.
2. Вычислите 
Для этого наберите в командной строке:
> cot(Pi/3)+tan(14*Pi/3);
Нажмите Enter. В результате в области вывода должно появиться число: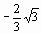 
.
3. Вычислите 
.
Для этого наберите в командной строке:
> combine((sin(Pi/8))^4+(cos(3*Pi/8))^4+
(sin(5*Pi/8))^4+ (cos(7*Pi/8))^4);
Нажмите Enter. (значение команды combine – преобразовывать выражения, например, со степенями). В результате в области вывода должно появиться число: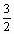 
.
§1.4 Преобразование математических выражений
Maple обладает широкими возможностями для проведения аналитических преобразований математических формул. К ним относятся такие операции, как приведение подобных, разложение на множители, раскрытие скобок, приведение рациональной дроби к нормальному виду и многие другие.
Выделение частей выражений.
Математическая формула, над которой будут производиться преобразования, записывается в следующей форме: >eq:=exp1=exp2; где eq – произвольное имя выражения, exp1 – условное обозначение левой части формулы, exp2 – условное обозначение правой части формулы.
Выделение правой части выражения осуществляется командой rhs(eq), выделение левой части выражения – командой lhs(eq). Рассмотрим пример:
> eq:=a^2-b^2=c;
eq:= 
> lhs(eq);
> rhs(eq);
с
Если задана рациональная дробь вида a/b, то можно выделить ее числитель и знаменатель с помощью команд numer и denom, соответственно. Пример:
> f:=(a^2+b)/(2*a-b);
> numer(f);
> denom(f);
Тождественные преобразования выражений.
Раскрытие скобок выражения eq осуществляется командой expand(eq). Пример:
> eq:=(x+1)*(x-1)*(x^2-x+1)*(x^2+x+1);
> expand(eq);
Разложение многочлена на множители осуществляется командой factor(eq). Пример:
> p:=x^5-x^4-7*x^3+x^2+6*x;
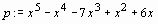
> factor(p);
Команда expand может иметь дополнительный параметр, позволяющий при раскрытии скобок оставлять определенное выражение без изменений. Например, пусть требуется каждое слагаемое выражения 
умножить на выражение (x+a). Тогда в командной строке следует написать:
> expand((x+a)*(ln(x)+exp(x)-y^2), (x+a));
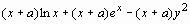
Дробь можно привести к нормальному виду с помощью команды normal(eq). Например:
> f:=(a^4-b^4)/((a^2+b^2)*a*b);
> normal(f);
Упрощение выражений осуществляется командой simplify(eq). Пример:
> eq:=(cos(x)-sin(x))*(cos(x)+sin(x)):
> simplify(eq);
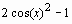
Приведение подобных членов в выражении осуществляется командой collect(exp,var), где exp – выражение, var – имя переменной, относительно которой следует собирать подобные. В команде simplify в качестве параметров можно указать, какие выражения преобразовывать. Например, при указании simplify(eq,trig) будет производиться упрощение при использовании большого числа тригонометрических соотношений. Стандартные параметры имеют названия: power – для степенных преобразований; radical или sqrt – для преобразования корней; exp – преобразование экспонент; ln – преобразование логарифмов. Использование параметров намного увеличивает эффективность команды simplify.
Объединить показатели степенных функций или понизить степень тригонометрических функций можно при помощи команды combine(eq,param), где eq – выражение, param – параметры, указывающие, какой тип функций преобразовать, например, trig – для тригонометрических, power – для степенных. Пример:
> combine(4*sin(x)^3, trig);
Для упрощения выражений, содержащих не только квадратные корни, но и корни других степеней, лучше использовать команду radnormal(eq). Пример:
> sqrt(3+sqrt(3)+(10+6*sqrt(3))^(1/3))=
radnormal(sqrt(3+sqrt(3)+(10+6*sqrt(3))^(1/3)));
С помощью команды convert(exp, param), где exp – выражение, которое будет преобразовано в указанный тип param. В частности, можно преобразовать выражение, содержащее sin x и cos x, в выражение, содержащее только tg x, если указать в качестве параметра tan, или, наоборот, tg x, ctg x можно перевести в sin x и сos x, если в параметрах указать sincos.
Вообще, команда convert имеет более широкое назначение. Она осуществляет преобразование выражения одного типа в другой. Например: convert(list, vector) – преобразование некоторого списка list в вектор с теми же элементами; convert(expr, string) – преобразование математического выражения в его текстовую запись. Для вызова подробной информации о назначении параметров команды convert следует обратиться к справочной системе, набрав convert[termin].
Если вы забыли параметры какой-либо команды, то можно воспользоваться справочной системой Maple. Для вызова справки по конкретной команде, следует выделить набранное имя этой команды и нажать клавишу F1. Если команда набрана правильно, то появится описание этой команды (в большинстве версий Maple помощь на английском языке).
Задание 4.
1. Перейдите в текстовый режим и наберите “Задание №4”. После не забудьте перейти в режим командной строки. Перед выполнением каждого пункта этого задания обязательно набирайте команду обновления restart;
2. Разложить полином на множители 
. Для этого наберите в командной строке:
> factor(x^3+4*x^2+2*x-4);
После нажатия клавиши Enter должно получиться 
.
3. Упростить выражение 
. Наберите:
> eq:=(1+sin(2*x)+cos(2*x))/(1+sin(2*x)-cos(2*x)):
> convert(eq, tan):
> eq=normal(%);
.
4. Упростить выражение 
. Для этого наберите:
> eq:=3*(sin(x)^4+cos(x)^4)-2*(sin(x)^6+cos(x)^6):
> eq=combine(eq, trig);
5. Выполните все контрольные задания. Перед их выполнением не забудьте набрать в текстовом режиме “Контрольные задания”. Результаты выполнения заданий покажите преподавателю.
6. Сохраните файл со всеми выполненными заданиями на диск.
7. Ответьте на все контрольные вопросы.
Контрольные задания
1. Вычислить: 
.
2. Вычислить: 
.
3. Вычислить точное и значение выражения: 
.
4. Записать формулы: 
; 
.
5. Разложить на множители полином 
.
6. Упростить выражение 
Контрольные вопросы
- Что такое Maple и для чего он предназначен?
- Опишите основные элементы окна Maple.
- На какие условные части делится рабочее поле Maple и что в этих частях отображается?
- Как перевести командную строку в текстовую и наоборот?
- В каком режиме проходит сеанс работы в Maple?
- Перечислите пункты основного меню Maple и их назначение.
- Какое стандартное расширение присваивается файлу рабочего листа Maple?
- Как представляются в Maple основные математические константы?
- Опишите виды представления рационального числа в Maple.
- Как получить приближенное значение рационального числа?
- Какими разделительными знаками заканчиваются команды в Maple и чем они отличаются?
- Какой командой осуществляется вызов библиотеки подпрограмм?
- Объясните назначение команд factor, expand, normal, simplify, combine, convert.
