КОМПЬЮТЕРНАЯ ЛОГИКА
Группа 6 (11)
Практическая работа 4
Тема: Перевод правильных дробей
Цель: Повторить изученный материал. Изучить новый теоретический материал. Научиться выполнять операции с неправильными дробями в различных системах счисления
Теоретический материал законспектировать в тетрадь
Перевод из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную:
а) исходная дробь умножается на основание системы счисления, в которую переводится (2, 8 или 16);
б) в полученном произведении целая часть преобразуется в соответствии с таблицей в цифру нужной системы счисления и
отбрасывается – она является старшей цифрой получаемой дроби;
в) оставшаяся дробная часть (это правильная дробь) вновь умножается на нужное основание системы счисления с
последующей обработкой полученного произведения в соответствии с шагами а) и б);
г) процедура умножения продолжается до тех пор, пока ни будет получен нулевой результат в дробной части произведения
или ни будет достигнуто требуемое количество цифр в результате;
д) формируется искомое число: последовательно отброшенные в шаге б) цифры составляют дробную часть результата,
причем в порядке уменьшения старшинства.
В некоторых случаях можно рекомендовать упрощенные способы перевода чисел из одной системы счисления в другую.
Системы счисления называются кратными, если выполняется соотношение: S = RN, где S, R – основания систем счисления, N – степень кратности (целое число: 2, 3 …).
Правило перевода дробных чисел
Отдельно переводится целая часть числа, отдельно - дробная. Результаты складываются.
Задания для самостоятельного выполнения(сдать на листе)
Задание 1. Выполнить перевод из десятичной системы счисления в шестнадцатеричную числа 19,847. Перевод выполнять до трех значащих цифр после запятой.
Решение выполняем по алгоритму:
1)Представим исходное число как сумму целого числа и правильной дроби:
19,847 =
2) Выполним перевод отдельно целой и дробной части числа:
19 =
0,847 =
Тогда имеем:
19 + 0,847 =
Таким образом, 19,847 =
Задание 2. Выполнить перевод из десятичной системы счисления в шестнадцатеричную числа 118,47 по алгоритму из задания 1.
Задание 3.
А)Перевести 23,125(10) в двоичную систему счисления по алгоритму из задания 1. Б)Перевести десятичную дробь А = 49,625 в двоичную систему счисления (q2=2)
Задание 4. Сколько единиц в двоичной записи десятичного числа 14,125? Для решения выполнить перевод числа по алгоритму из задания 1, после чего посчитать количество единиц в результате.
Задание 5. Перевести 23.12510  2 с.с.
2 с.с.
Написать вывод о проделанной работе.
Задание 1. Выполнить перевод из десятичной системы счисления в шестнадцатеричную числа 19,847. Перевод выполнять до трех значащих цифр после запятой.
Представим исходное число как сумму целого числа и правильной дроби:
19,847 = 19 + 0,847.
Как следует из примера 3.2, 19 = 1316; а в соответствии с примером 3.9 0,847 = 0,D8D16. Тогда имеем:
19 + 0,847 = 1316 + 0,D8D16 = 13,D8D16.
Таким образом, 19,847 = 13,D8D16.
Задание 2. Выполнить перевод из десятичной системы счисления в шестнадцатеричную числа 118,47
11810=7616, 0,4710=0,7816, значит, 118,4710=76,7816.
Задание 3. Перевести 23,125(10) в двоичную систему счисления


Задание 4. Сколько единиц в двоичной записи десятичного числа 14,125?
Решение:
Переведем целую часть числа в двоичную систему:

Переведем дробную часть числа в двоичную систему:
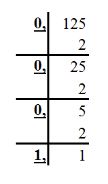
Соединим целую и дробную части:
14,12510 = 1110,0012
Количество единиц равно 4.
Ответ: 4
Задание 5. Перевести 23.12510  2 с.с.
2 с.с.
| 1. Переведем целую часть: | 2. Переведем дробную часть: | 3. Таким образом: |

| 
| 2310 = 101112; 0.12510 = 0.0012. Результат: 23.12510 = 10111.0012. |
Пример 9. Перевести десятичную дробь А = 49,625 в двоичную систему счисления (q2=2)
Решение. Результаты перевода соответственно целой и дробной частей возьмем из примеров 5 и 7.
Ответ: А2= 110001,1010.






