КОМПЬЮТЕРНАЯ ЛОГИКА
Группа 6 (11)
Практическая работа 4
Тема: Перевод правильных дробей
Цель: Повторить изученный материал. Изучить новый теоретический материал. Научиться выполнять операции с правильными дробями в различных системах счисления
Теоретический материал законспектировать в тетрадь
Правильную дробь 
, имеющую в системе с основанием s вид 
, можно выразить в системе счисления с основанием h как многочлен вида
Старшая цифра 
может быть найдена умножением этого многочлена на h, т.е.
Если это произведение меньше 1, то цифра равна 0, если же оно больше или равно 1, то цифра равна целой части произведения. Следующая цифра справа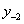 
определяется путём умножения дробной части указанного выше произведения на h и выделения его целой части и т.д. Процесс может оказаться бесконечным, т.к. не всегда можно представить дробь по основанию h конечным набором цифр.
Для перевода правильной дроби из системы счисления с основанием s в систему счисления с основанием h нужно умножать исходную дробь и дробные части получающихся произведений на основание h (по правилам "старой" s-системы счисления). Целые части полученных произведений дают последовательность цифр дроби в h-системе счисления.
Описанная процедура продолжается до тех пор, пока дробная часть очередного произведения не станет равной нулю либо не будет достигнута требуемая точность изображения числа X в h -ичной системе счисления. Представлением дробной части числа X в новой системе счисления будет последовательности целых частей полученных произведений, записанных в порядке их получения и изображённых h -ичной цифрой. Абсолютная погрешность перевода числа X при p знаков после запятой равняется 
.
Пример 2. Перевести правильную дробь 0,453 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.
* В двоичную систему:
Ответ: 
** В восьмеричную систему:
Ответ: 
*** В шестнадцатеричную систему:
Ответ: так как 
, то 
Очевидно, что этот процесс может продолжаться бесконечно, давая все новые и новые знаки в изображении двоичного эквивалента числа 0,710. Так, за четыре шага мы получаем число 0,10112, а за семь шагов число 0,10110012, которое является более точным представлением числа 0,710 в двоичной системе счисления, и т.д. Такой бесконечный процесс обрывают на некотором шаге, когда считают, что получена требуемая точность представления числа.
Пример 1. Перевести число 0,847 в двоичную, восьмеричную и шестнадцатеричную системы счисления. Перевод выполнить
до трех значащих цифр после запятой.
10 => 2
Если записывать последовательные произведения друг под другом и отделить чертой целую и дробную части, то слева от черты, читая сверху вниз, получим двоичный эквивалент переводимой дроби. Для примера переведем в двоичную систему десятичное число 0,35:
0 35
0 70
1 40
0 80
1 60
1 20
0 40
0 80
1 60
Поясним это: 0,35·2=0,70, следовательно, 0 - первая цифра после запятой в переводимой дроби. Далее 0,70·2=1,40. Значит, следующая цифра 1. Затем 0,40·2=0,80. Следующая цифра 0 и т.д.
Выписывая цифры полученного столбца сверху вниз, получим:
0,35≈0,010110012.
Здесь стоит знак приближенного равенства, т.к. мы ограничились восемью двоичными цифрами после запятой, в то время как точный перевод в данном случае представляет собой бесконечную периодическую двоичную дробь.
Задания для самостоятельного выполнения (Сдать на листах)
Задание 1. Заполните таблицу, в каждой строке которой одно и то же дробное число должно быть записано в различных системах счисления.
| Двоичная | Восьмеричная | Десятичная | Шестнадцатеричная |
| 0,101 | |||
| 0,6 | |||
| 0,125 | |||
| 0,4 | |||
| 0,110011 | |||
| 0,09 | 0,3564 | ||
| 0,1С |
Задание 2.
a)Перевести число 0,6562510 в восьмеричную систему счисления.
b)Перевести 0,3125(10) в восьмеричную систему счисления
Задание 3. Перевести число 0,6562510 в шестнадцатеричную систему счисления.
Задание 4.
a)Перевести десятичную дробь 0,562510 в двоичную систему счисления.
b)Перевести десятичную дробь А = 0,5625 в двоичную систему счисления (q2=2)
c)Перевести десятичную дробь А = 0,625 в двоичную систему счисления (q2=2)
d)Перевести 0,65(10) в двоичную систему счисления с точностью до 6 зна-ков
e)Перевести двоичную дробь А2= 0,1101 в десятичную систему счисления. Основаниеq2 изображается в двоичной системе эквивалентомq2=10102.
Задание 5. Перевести в двоичную систему счисления десятичную дробь 0.710.
Задание 6. Перевести числа 0,47 и 0,75 из десятичной системы счисления в двоичную (до четырех знаков после запятой)
Задание 7.
0,100111010 2 =?8 =?16.
Задание 8.
а) 0,2510 =?2.
б) 0,0101012 =?10.
