1) Обчислимо визначник матриці 
.
Оскільки 
, то існує обернена матриця.
2)Знаходимо алгебраїчні доповнення елементів матриці
; 
; 
; 
; 
; 
; 
; 
.
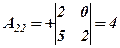3) Записуємо нову матрицю за формулою (3)
.
4) За формулою (4) отримуємо обернену матрицю
.
5) перевіримо, що 
,
Приклад 2. Знайти матрицю, обернену до матриці
.
Розв’язання. 1)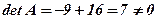 
.
2) 
; 
;
; 
.
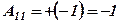3) 
.
4) 
.
5) 
.
Приклади для самостійного розв’язання
Знайти обернені матриці для матриць:
1.. 2.. 3..
4.. 5.. 6..
7..
Відповіді:
1.. 2. 3..
4. 
..5. 
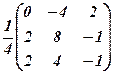. 6.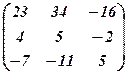 
7..
Розв’язування систем лінійних рівнянь
Матричним способом
Обмежимось розглядом системи 3-х лінійних рівнянь
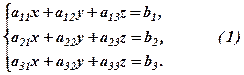
Запишемо такі матриці:
,
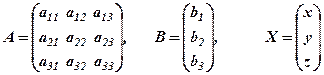де складена з коефіцієнтів при невідомих — матриця системи, 
– матриця вільних членів, 
– матриця невідомих. Знайдемо добуток
Користуючись означенням рівності матриць, ми бачимо, що система ЛР (1) є не що інше, як рівність відповідних елементів матриць – стовпців 
і . Тому початкова система (1) набуває форму матричного рівняння
Для розв’язання останнього домножимо зліва рівняння (2) на обернену матрицю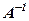 
, вважаючи, що 
, отримаємо
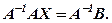
Але 
, а 
, тоді розв’язок матричного рівняння (2) запишеться
(3)
Покажемо, що з формули (3) можна отримати формули Крамера. Дійсно, підставляючи в (3) вирази для 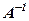і , маємо
За теоремою про заміщення кожний елемент останньої матриці дорівнює значенням допоміжних визначників 
, які були введені при розв’язуванні систем за формулами Крамера. Тому далі маємо
Звернемо увагу на те, що в формулі (3) співмножник 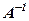, залежить тільки від коефіцієнтів при невідомих, а тільки від вільних членів. Тому, коли приходиться розв’язувати системи вигляду (1) з однаковими лівими частинами і різними вільними членами, то в таких випадках матричний розв’язок (3) стає зручнішим: обернену матрицю 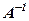знаходимо тільки один раз і перемножуємо на нову матрицю . В той же час, за формулами Крамера прийшлося б заново обчислювати допоміжні визначники відповідно для кожного нового набору вільних членів.
Приклад 1. Розв’язати систему рівнянь матричним способом
Складемо матрицю системи
Для цієї матриці в 1.12. ми вже знайшли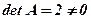 
і обернену матрицю
Тому згідно (3) маємо
Отже, 
Пропонуємо перевірити відповідь.
Приклад 2. Розв’язати матричним способом систему
Розв’язання. Запишемо матриці
, 
, 
.
У матричному вигляді система запишеться
.
Визначник матриці 
, існує обернена матриця 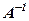. Її алгебраїчні допованення
; 
;
; 
.
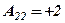Обернена матриця
.
Розв’язком системи є матриця
.
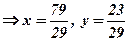Перевірка: 
,
.
Зауваження.
1. Розглянутий матричний спосіб на прикладі лінійних систем третього порядку узагальнюється на системи вищих порядків.
2. В більш загальних випадках в матричних рівняннях
матриці і можуть мати інші розміри і бути не тільки матрицями стовпцями.
3. При розв’язанні матричних рівнянь вигляду
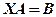
домножують на обернену матрицю 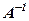справа, тобто
.
