Лабораторная работа № 20
1. Цель работы: закрепление теоретических знаний по теме 4.4. “Дифракция Фраунгофера”
приобретение практических навыков
изучение методики расчетов
2. Порядок подготовки к выполнению работы изучить тему и материал лабораторной работы
3. Порядок выполнения лабораторной работы
4. Подведение итогов выполнения работы
предъявить результаты, подготовка и оформление отчета, заполнить таблички, произвести обработку результатов измерений
5. техника безопасности при выполнении лабораторной работы
1. Цель работы. Изучение явления дифракции световых волн на узкой плоскопараллельной щели и на дифракционной решетке; экспериментальная проверка выполнимости условий для максимумов и минимумов дифракции; определение опытным путем длины волны излучения и периода дифракционной решетки.
2. Подготовка к работе. Перед выполнением лабораторной работы изучите явление дифракции, принцип Гюйгенса – Френеля, условия минимумов и максимумов в случае дифракции на узкой щели и на дифракционной решетке ([1], §118 – 120, 125 – 126; [2], гл. 8 – 11). Ознакомьтесь с устройством лабораторного стенда и методами измерений. Подготовьте ответы на вопросы к допуску.
3. Вопросы для допуска к лабораторной работе
1. В чем заключается явление дифракции? Каким образом на основании принципа Гюйгенса – Френеля можно объяснить образование дифракционной картины при прохождении световой волны через узкую щель?
2. Рассчитайте величину угла φ для минимума первого порядка при дифракции света с длиной волны λ = 0,63 мкм на плоскопараллельной щели шириной d = 0,05 мм.
3. Рассчитайте величину угла φ для главного максимума второго порядка в случае дифракционной решетки с периодом d = 8 мкм, если длина волны λ = 0,63 мкм.
4. Как будут изменяться положения максимумов на дифракционной картине от узкой щели, если передвигать щель ближе к экрану, не изменяя положений экрана и источника?
5. Объясните метод экспериментального определения длины волны излучения и периода дифракционной решетки.
4. Литература
1. Савельев И.В. Курс общей физики. Т. 2. М.: Наука, 1982.
2. Борн М., Вольф Э. Основы оптики. М.: Наука, 1973.
5. Методика проведения эксперимента и описание установки
Дифракцией называется совокупность не укладывающихся в рамки законов геометрической оптики явлений, наблюдаемых при распространении света в среде с резкими неоднородностями. В случае непрозрачных препятствий, например, щелей или отверстий, дифракция приводит к огибанию световыми волнами этих препятствий и проникновению света в область геометрической тени. В результате дифракции на экране за препятствием образуется дифракционная картина с регулярно расположенными в пространстве максимумами и минимумами интенсивности света.
Различают два типа дифракции: если фронт падающей на препятствие волны плоский, а экран расположен на расстоянии, значительно превышающем размеры препятствия, то говорят о дифракции Фраунгофера или о дифракции в параллельных лучах. В случае сферического фронта волны говорят о дифракции Френеля.
Для объяснения явления дифракции можно воспользоваться принципом Гюйгенса – Френеля. Согласно этому принципу, волновой фронт представляется в виде совокупности большого числа вторичных когерентных источников, излучающих вторичные волны в сторону распространения волны. В этом случае образование дифракционной картины является результатом интерференции излучений от вторичных источников, а интенсивность в каждой точке экрана зависит от разностей фаз между волнами, приходящими в эту точку от вторичных источников.
На рис. 1 показано характерное распределение интенсивности в дифракционной картине от узкой щели при падении на нее плоской световой волны в случае, когда расстояние от щели до экрана L значительно превышает ширину щели b (дифракция Фраунгофера). Результат интерференции волн от вторичных источников в некоторой точке экрана О (рис. 2) зависит от разности фаз между практически параллельными световыми лучами, идущими от вторичных источников, расположенных на открытом участке щели АВ. Эта разность фаз, в свою очередь, определяется разностью хода между лучами. Например, для вторичных источников, расположенных в точках А и В, указанная разность хода равна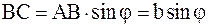 
.
Строгий анализ явления интерференции излучения от вторичных источников приводит к следующему распределению интенсивности в дифракционной картине от узкой щели:
 ,
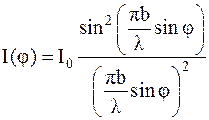| (1) |
где I0 — интенсивность в середине основного максимума, b — ширина щели, λ — длина волны излучения. Из формулы (1) следует, что минимумы интенсивности на дифракционной картине (I = 0) наблюдаются при условии
 ,
|
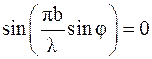то есть при углах
 .
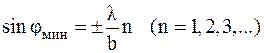| (2) |
Целое число n в формуле (2) называется порядком минимума.
Из рис. 1 следует, что 
, и поскольку при малых углах 
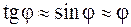, то условие минимума (2) можно записать в виде
 ,
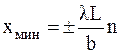| (3) |
где xмин — координата минимума на дифракционной картине.
Соотношение (3) позволяет экспериментально определить длину волны падающего на щель излучения следующими двумя способами.
Снимая экспериментальную зависимость xмин (L) и определяя коэффициент ее наклона
 ,
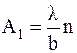| (4) |
получаем:
 .
| (5) |
Экспериментальная же зависимость xмин (n) имеет коэффициент наклона
 .
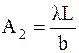| (6) |
Тогда находим
 .
| (7) |
Система из N лежащих в одной плоскости одинаковых параллельных узких щелей ширины b, разделенных непрозрачными промежутками ширины a, называется дифракционной решеткой. Интерференция вторичных волн от соседних щелей решетки приводит к появлению на экране ярких регулярно расположенных линий, называемых главными максимумами (рис. 3).
Для главных максимумов выполняется следующее условие:
 ,
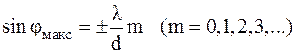| (8) |
где φмакс — угол наблюдения максимума из центра решетки, d = a + b — период решетки, целое число m называется порядком максимума.
Для малых углов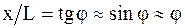 
, и условие (8) можно записать в виде
 .
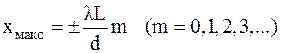| (9) |
Здесь координата максимумов xмакс отсчитывается от середины центрального максимума дифракционной картины.
Экспериментальная зависимость xмакс (m) координаты главного максимума от порядка максимума является линейной и имеет коэффициент наклона, равный
 .
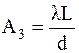| (10) |
Это дает возможность при известных значениях λ и L определить период дифракционной решетки d:
 .
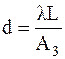| (11) |
Перейдем теперь к описанию лабораторного стенда и методики измерений. Схема установки изображена на рис. 4.
На оптической скамье 1 располагаются: источник световых волн — газовый гелий–неоновый лазер 2, оптический столик 3 и перемещаемый вдоль скамьи держатель 4, на котором закрепляются дифракционная щель или дифракционная решетка. Оптический столик снабжен неподвижной шкалой, вдоль которой с помощью регулировочного винта 5 может перемещаться экран 6 с прорезью для фотодатчика 7. Фотодатчик подсоединен к микроамперметру 8, показания которого пропорциональны интенсивности света, падающего на фотодатчик. Таким образом, измерительная система позволяет фиксировать пространственные положения дифракционных максимумов и минимумов, а также измерять относительные интенсивности света в различных точках дифракционной картины.
6. Порядок выполнения работы
6.1. Подготовка установки к работе (выполняет лаборант).
1. Включить лазер.
2. Установить держатель с фотодатчиком на деление "0" по шкале оптической скамьи.
3. Не включая микроамперметр, регулировочным винтом 5 совместить прорезь фотодатчика с нулевой отметкой на шкале экрана.
4. Пользуясь регулировочными винтами на корпусе лазера, совместить светящееся пятно с центром прорези фотодатчика.
5. Регулировочным винтом отвести прорезь фотодатчика на 3 см по шкале экрана вправо.
6.2. Измерение зависимости положения xмин дифракционных минимумов от расстояния L между щелью и экраном.
1. Установить держатель дифракционной щели на деление "60 см" по шкале оптической скамьи (прорезь фотодатчика остается смещенной на 3 см вправо от нуля на шкале экрана).
2. При помощи винтов раздвинуть зажимы и закрепить дифракционную щель в держателе таким образом, чтобы пятно лазерного луча освещало середину щели, а дифракционная картина на экране была наиболее отчетлива.
3. Отрегулировать ширину щели b, вращая винт на корпусе щели, таким образом, чтобы минимум третьего порядка (n = 3) совпадал с делением "2 см" на шкале экрана. Записать значения L1 = 0,6 м,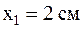 
и b в таблицу 1.
| Таблица 1 | ||||||||
| L, м | 0,6 | 0,5 | 0,4 | 0,3 | 0,2 | |||
| xмин, мм | ||||||||
| b = | λ = | |||||||
4. Не изменяя ширины щели, измерить положения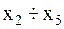 
дифракционного минимума третьего порядка (n = 3) для четырех других положений держателя щели (L = 0,5 м; 0,4 м; 0,3 м; 0,2 м). Данные записать в таблицу 1.
6.3. Измерение зависимости положения xмин дифракционных минимумов узкой щели от их порядка n.
1. Установить держатель с дифракционной щелью в положение L = 50 см по шкале оптической скамьи.
2. С помощью винта на корпусе щели отрегулировать ширину щели b таким образом, чтобы минимум пятого порядка (n = 5) совпадал с делением "2 см" по шкале экрана. В случае необходимости повторно отрегулировать положение щели в держателе, добиваясь максимально яркой дифракционной картины. Записать значение b в таблицу 2.
| Таблица 2 | ||||||||
| n | ||||||||
| xмин, мм | ||||||||
| b = | λ = | |||||||
3. Путем визуального наблюдения по шкале экрана определить положения дифракционных минимумов порядков n = 1 ÷ 5. Результаты записать в таблицу 2.
6.4. Измерение зависимости интенсивности света I от угла φ в пределах центрального максимума дифракционной картины от узкой щели.
1. Установить держатель щели на деление "60 см" по шкале оптической скамьи.
2. Пользуясь винтом на корпусе щели, отрегулировать ширину щели b таким образом, чтобы минимум первого порядка (n = 1) совпадал с делением "1 см" на шкале экрана. Отрегулировать положение корпуса щели в держателе, добиваясь максимально яркого изображения дифракционной картины на экране. Записать значение b в таблицу 3.
3. Включить микроамперметр и установить переключатель диапазонов микроамперметра в положение "10". С помощью регулировочного винта установить прорезь фотодатчика в положение "0", совпадающее с центром основного максимума дифракционной картины. Записать в таблицу 3 измеренное по шкале микроамперметра значение 
.
| Таблица 3 | |||||||||||
| x, мм | |||||||||||
| IЭ | |||||||||||
| |||||||||||
| |||||||||||
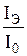
| b = | bЭ = |
4. Перемещая регулировочным винтом прорезь фотодатчика с шагом 1 мм вдоль дифракционной картины, снять показания микроамперметра IЭ в пределах расстояний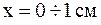 
. Данные записать в таблицу 3.
5. Выключить микроамперметр.
6.5. Измерение положений главных максимумов xмакс при прохождении излучения через дифракционную решетку.
1. Удалив из держателя дифракционную щель, установить в держатель дифракционную решетку таким образом, чтобы лазерный луч проходил через ее центральную часть.
2. Установить держатель в положение L = 20 см по шкале оптической скамьи.
3. Путем визуального наблюдения измерить по шкале на экране положения xмакс главных максимумов порядков m = 1, 2, 3. Данные записать в таблицу 4.
| Таблица 4 | ||||||
| m | ||||||
| xмакс, мм | ||||||
| d = | ||||||
7. Оформление отчёта
1. По данным таблицы 1 построить график зависимости xмин (L), и, определив коэффициент наклона графика A1, рассчитать по формуле (5) длину волны λ. Записать значение λ в табл. 1.
2. По данным таблицы 2 построить график зависимости xмин (n), и, определив коэффициент наклона графика A2, рассчитать по формуле (7) длину волны λ. Записать значение λ в табл. 2.
3. Используя значения величин λ, записанных в табл. 1 и 2, рассчитать среднее значение длины волны λср. Сравнить полученное значение λср с действительной длиной волны лазерного излучения λ = 0,628 мкм.
4. Для эксперимента по пункту 6.4 рассчитать ширину щели bЭ по формуле (3), принимая n = 1, xмин = 1 см, λ = 0,628 мкм. Записать полученное экспериментальное значение bЭ в таблицу 3. Сравнить экспериментальное значение ширины щели bЭ с записанным ранее истинным значением b.
5. По данным таблицы 3 рассчитать относительные интенсив-ности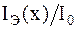 
для различных расстояний x. Полученные величины занести в табл. 3.
6. Пользуясь формулой (1), произвести расчет теоретических значений 
для всех значений координаты x. При расчетах учесть соотношение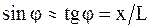 
. Полученные величины занести в табл. 3.
7. По данным таблицы 3 построить на одном рисунке экспериментальный 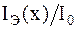и теоретический графики относительной интенсивности главного максимума. Сравнить полученные кривые.
8. По данным таблицы 4 построить график зависимости xмакс (m), и, определив коэффициент наклона графика A3, рассчитать по формуле (11) длину периода дифракционной решетки d. При расчетах принять λ = 0,628 мкм. Полученную величину d занести в табл. 4.
9. По результатам эксперимента сделать выводы.
