Нулевая гипотеза в этом случае заключается в том, что все m генеральных совокупностей, из которых взяты выборки, имеют равные дисперсии, т.е. σ21 = σ22 = … = σ2m = σ2.
Задание 5
Испытано на растяжение 5 серий по 20 образцов. Значения выборочных дисперсий составляют: s 21 = 88; s 22 = 105; s 23 = 94; s 24 = 197.Требуется проверить гипотезу о равенстве генеральных дисперсий предела прочности материала при альтернативной гипотезе σ21 ≠ σ22.
По формуле (3.11)
F max =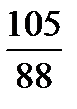 
= 1,1932
По таблице 3.4 для α = 0,05; m = 3 и k = 30 – 1 = 29
F max 0.05 = 4,05
Условие (3.11) выполняется
Заключение: дисперсии равны друг другу.
Критерий Кочрена. Используется также при равных объёмах отдельных выборок и является предпочтительным по сравнению с критерием Хартлея в случаях, когда одна из выборочных дисперсий значительно больше остальных, а также при m > 12.
Находят статистику
G max = 
≤ G α. (3.12)
При выполнении неравенства нулевую гипотезу не отвергают. В противном случае – отвергают и принимают альтернативную гипотезу.
Задание 6
Проверить нулевую гипотезу Н 0: σ21 = σ22 = … = σ2 по условию примера 3.5
По формуле (3.12)
G max = 
= 0,3659
По таблице 3.5 для α = 0,05; m = 5 и k = 20 – 1 = 19
G α = G 0,05 = 0,4999
Условие (3.12) выполняется
Заключение: гипотеза принимается.
Задание 7
Для условий примера 3.4 проверить гипотезу о равенстве средних значений. (n 1 = 28,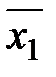 
= 47, s 21 = 82; n 2 = 30, 
= 45, s 22 = 105).
При решении примера 3.4 было показано, что гипотеза о равенстве генеральных дисперсий (σ21 = σ22 = σ2) не противоречит опытным данным. В связи с этим по формуле (3.17) находим оценку генеральной дисперсии и среднего квадратического отклонения:
s 2 = 
= 96,8036;
s = 
= 9,8389.
По формуле (3.18) вычисляем статистику
t = 
= 0,7736
.
Задавшись α = 0,1 (для k = 30 + 28 – 2 = 56> 30 t α ≈ z 1–α/2), по таблице 2.8 находим критическое значение t 0,1 = 1,645.
В связи с тем, что условие (3.19) не выполняется, нулевую гипотезу о равенстве средних значений отвергаем.
Задание 8
По результатам испытаний провести дисперсионный анализ с целью проверки равенства средних значений
| n i | 
| s 2i | |||||||||
| 12,86 | |||||||||||
| 165,5 | 13,10 | ||||||||||
| 157,17 | 15,77 | ||||||||||
| 166,14 | 26,48 | ||||||||||
| 161,8 | 50,70 | ||||||||||
| 16,50 | |||||||||||
| 159,71 | 20,24 | ||||||||||
| 172,33 | 13,07 | ||||||||||
| 53,50 | |||||||||||
| 166,83 | 15,37 | ||||||||||
| 161,29 | 25,24 |
Учитывая, что в каждой партии число образцов n i ≥ 5 и объёмы выборокнеодинаковые, проверку однородности дисперсий производим по критерию Бартлета
По формуле (3.13) вычисляем статистику
χ2 =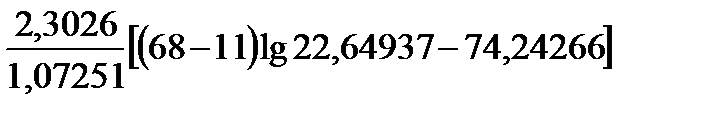 
= 6,431202,
где с = 1 + 
= 1,07251;
s 2 = 
= 22,6494.
В таблице 2.10 для α = 0,1 и числа степеней свободы k = m – 1 = 10
χ20,01 = 16
Условие (3.16) выполняется
χ2 = 6,431202 < χ20,01 = 16
Следовательно дисперсии можно считать однородными.
Оценку генерального среднего производим по формуле (3.21)
= 
= 163,41.
Межпартийная компонента дисперсии (3.22) (число степеней свободы k 1 = 11 – 1 = 10)
s 21 = 
= 134,1456.
Внутрипартийная (остаточная) компонента дисперсии (3.23) (число степеней свободы k 2 =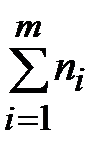 
– m = 68– 11 = 57)
s 22 = 
= 22,6494
Дисперсионное отношение
F = s 21 / s 22 = 5,922708.
Меньше табличного (таблице 3.3)
В этом случае все рассматриваемые результаты испытаний принадлежат одной генеральной совокупности, распределённой нормально с параметрами
= 163,41.
s 2 = 22,64937.
