1. Для фіксованого натурального числа k на множині N визначимо відношення R: (m, n)Î R тоді і тільки тоді, коли
m - n ділиться на k. Довести, що відношення R є відношенням еквівалентності на N.
2. На множині N ´ N визначимо відношення R і Q:
(а) ((a, b),(c, d))Î R Û a + d = b + c;
(б) ((a, b),(c, d))Î Q Û a×d = b × c.
Довести, що відношення R і Q є відношеннями еквівалентності на множині N ´ N.
3. Нехай M = N ´ N. Означимо на множині M відношення R таким чином: (a, b) R (c, d) тоді і тільки тоді, коли
(а) ab = cd; б) a + b = c + d.
Довести, що R є еквівалентністю на M. Виписати всі елементи класів еквівалентності [(1,1)], [(2,2)], [(4,3)], [(1,23)] і [(6,8)] за відношенням R.
4. На множині дійсних чисел означимо відношення H: xHy тоді і тільки тоді, коли (x - y) - раціональне число. Довести, що відношення H є відношенням еквівалентності.
5. На множині N натуральних чисел означимо відношення R: mRn тоді і тільки тоді, коли m / n = 2 k для деякого цілого k.
(а) Довести, що R є відношенням еквівалентності на N.
(б) Скільки різних класів еквівалентності є серед [1] R, [2] R, [3] R і [4] R?
(в) Скільки різних класів еквівалентності є серед [6] R, [7] R, [12] R, [24] R, [28] R, [42] R і [48] R?
6. Нехай у множині M зафіксовано деяку підмножину K Í M. Означимо відношення R на b(M): ARB тоді і тільки тоді, коли A Ç K = B Ç K, A, B Îb(M).
(а) Довести, що R є відношенням еквівалентності на b(M).
(б) Для M = {1,2,3} і K = {1,2} знайти класи еквівалентності за відношенням R.
(в) Для M = {1,2,3,4,5} і K = {1,2,3} визначити [ A ] R, де A = {2,3,4}.
(г) Для M = {1,2,3,4,5} і K = {1,2,3} визначити кількість класів еквівалентності та кількість підмножин множини M у кожному класі еквівалентності за відношенням R.
(д) Визначити кількість класів еквівалентності та кількість підмножин множини M у кожному класі еквівалентності за відношенням R, якщо | M |= n і | K |= m.
7. Нехай M множина всіх прямих на площині. Чи будуть еквівалентностями на M такі відношення:
(а) паралельність прямих; (б) перпендикулярність прямих?
8. Довести, що відношення рівності iM на будь-якій множині M є відношенням еквівалентності.
9. Довести, що для довільного відношення еквівалентності R на множині M виконується iM Í R. Таким чином, iM є найменшим відношенням еквівалентності на множині M.
10. Довести, що відношення рівнопотужності множин є еквівалентністю.
11. Довести, що еквівалентністю є відношення подібності на множині всіх трикутників.
13. Довести, що R є відношенням еквівалентності тоді і тільки тоді, коли R- 1 є відношенням еквівалентності.
14. Довести, що перетин будь-якої сукупності відношень еквівалентності на множині M є еквівалентністю на M.
15. Навести приклад двох еквівалентностей R 1 і R 2 на множині M ={1,2,3,4}таких, що R 1È R 2 не є еквівалентністю на множині M.
16. Довести, що об’єднання R 1È R 2 двох еквівалентностей R 1 і R 2 є еквівалентністю тоді і тільки тоді, коли R 1È R 2= R 1° R 2.
17. Довести, що для довільного відношення еквівалентності R виконується R ° R = R.
18. Навести приклад двох еквівалентностей R 1 і R 2 на множині M ={1,2,3,4}таких, що R 1° R 2 не є еквівалентністю на M.
19. Довести, що композиція R 1° R 2 двох еквівалентностей R 1 і R 2 є еквівалентністю, якщо R 1° R 2 = R 1È R 2.
20. Довести, що композиція R 1° R 2 двох еквівалентностей R 1 і R 2 є еквівалентністю тоді і тільки тоді, коли
(а) R 1° R 2 = R 2° R 1; (в) R 2° R 1 Í R 1° R 2;
(б) R 1° R 2 - симетричне відношення; (г) R 1° R 2 = R 1° R 2 È R 2° R 1.
21. Довести, що коли R 1 і R 2 - еквівалентності, то відношення (R 1È R 2)* також буде еквівалентністю.
22. Довести, що коли R 1 і R 2 - еквівалентності, то відношення (R 1° R 2È R 2° R 1)* також буде еквівалентністю.
23. Довести, що коли R 1 і R 2 - еквівалентності, то (R 1È R 2)* = (R 1° R 2È R 2° R 1)*.
24. Довести, що коли R 1 і R 2 - еквівалентності і R 1° R 2 = R 2° R 1, то R 1° R 2 = (R 1È R 2)*.
25. Нехай R 1 і R 2 - еквівалентності і R 1° R 2= R 2° R 1. Довести, що R 1° R 2 є найменшим відношенням еквівалентності, яке містить R 1È R 2.
26. Нехай R 1 і R 2 - еквівалентності. Довести, що найменшим відношенням еквівалентності, яке містить R 1È R 2, є (R 1È R 2)*.
27. Нехай R 1 і R 2 - еквівалентності. Довести, що найменшим відношенням еквівалентності, яке містить R 1È R 2, є (R 1° R 2È R 2° R 1)*.
28. Довести, що для довільної сукупності відношень еквівалентності { Ri }, i Î I існує еквівалентність Q така, що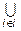 
Ri Í Q і для будь-якого відношення еквівалентності R з включення 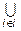Ri Í R випливає Q Í R (тобто Q є найменшим відношенням еквівалентності, яке містить 
Ri)
29. Побудувати найменше відношення еквівалентності Q на множині M = {1,2,3,4}, яке включає задане відношення R.
(а) R = {(2,4),(3,1)};
(б) R = {(1,1),(1,2),(2,3),(3,3)};
(в) R = {(1,2),(2,2),(1,3),(2,3),(4,2)}.
30. Довести, що для довільної сукупності еквівалентностей { Ri }, i Î I найменшою еквівалентністю Q, яка містить 
Ri, є відношення (
Ri)*.
31. Нехай задано довільне відношення R на множині M. Сформулювати алгоритм, який за допомогою основних операцій над відношеннями дозволяє побудувати найменше відношення еквівалентності Q на множині M таке, що R Í Q.
Застосувавши цей алгоритм до заданого відношення R на множині M ={1,2,3,4,5}, знайти відповідне відношення еквівалентності Q.
(а) R = {(1,1),(1,2),(4,2),(5,4)};
(б) R = {(2,4),(3,3),(3,2),(4,1),(4,2),(5,1),(5,5)};
(в) R = {(2,2),(3,3)}.
Для кожного з відношень Q побудувати фактор-множину M/Q.
32. Довести, що для довільного відношення R на множині M найменше відношення еквівалентності Q, яке містить R, дорівнює (R È iM È R- 1)*.
33. Знайти відношення R на множині M = {1,2,3,4}, яке містить мінімально можливу кількість елементів і таке, що найменшим відношенням еквівалентності Q, що включає R, є повне відношення на M, тобто Q = M ´ M.
34. Побудувати на множині M = { a 1, a 2,..., an } відношення R з мінімально можливою кількістю елементів таке, що найменше відношення еквівалентності Q, що містить R, збігається з повним відношенням на M, тобто Q = M ´ M.
35. Визначити мінімально можливу кількість елементів у відношенні R на множині M = { a 1, a 2,..., an }, для якого найменшим відношенням еквівалентності M, що містить R, є повне відношення на M, тобто Q = M ´ M.
Дати геометричну (графову) інтерпретацію відповіді.
36. Довести, що транзитивне замикання R * толерантного відношення R є відношенням еквівалентності.
37. Довести, що транзитивне замикання R * відношення еквівалентності R збігається з R, тобто R * = R.
38. Навести приклад відношення R на множині M = {1,2,3,4}, для якого виконується R * = R і яке не є еквівалентністю.
39. Нехай R 1 - толерантне відношення, R 2 - еквівалентність і R 1Í R 2. Довести, що R 1*Í R 2.
40. Довести, що найменшим відношенням еквівалентності Q, яке містить толерантне відношення R, є R *.
41. Нехай R 1 і R 2 - відношення еквівалентності на множині M. Довести, що відношення R 1° R 2° R 1 буде еквівалентністю тоді і тільки тоді, коли
(а) R 2° R 1° R 2Í R 1° R 2° R 1; (б) R 1° R 2° R 1 = R 1° R 2È R 2° R 1.
41. Нехай R транзитивне й симетричне відношення на множині M і Pr1 R ÈPr2 R=M. Довести, що R є еквівалентністю на множині M.
43. Довести, що коли R рефлексивне й транзитивне відношення на множині M, тоді R Ç R- 1 є відношенням еквівалентності на множині M.
44. Нехай R є відношенням на M. Довести, що R є еквівалентністю тоді і тільки тоді, коли (R ° R- 1) È iM = R.
45. Довести, що рефлексивне відношення R на множині M є еквівалентністю тоді і тільки тоді, коли з того, що xRy і xRz завжди випливає yRz, x, y, z Î M.
46. Довести, що для довільного відношення еквівалентності R виконується:
(а) x Î[ x ] R;
(б) (x, y)Î R Û [ x ] R = [ y ] R ;
(в) або[ x ] R = [ y ] R , або[ x ] R Ç [ y ] R =Æ.
47. Довести, що для довільного відношення еквівалентності R наведені твердження є рівносильними
(а) (x, y)Î R; (б) [ x ] R Ç[ y ] R ¹ Æ; (в) [ x ] R =[ y ] R.
48. Нехай f: A ® B - довільне відображення. Покладемо R ={(x, y) | f (x)= f (y)}. Довести, що R є еквівалентністю на множині A і для відображення f існує розклад f = e ° f 1, де e - природне відображення множини A на A / R, а f 1 - взаємно однозначна відповідність між A / R і f (A) (правило розкладу або факторизації відображення).
49. Нехай C - деяка відповідність між A і B. Означимо відношення RC на множині A таким чином: для x, y ÎPr1 C вважаємо (x, y)Î RC тоді і тільки тоді, коли C (x)Ç C (y)¹Æ.
Довести, що
(а) відношення RC симетричне;
(б) відношення RC рефлексивне тоді і тільки тоді, коли відповідність C всюди визначена;
(в) коли для деякого x Î A виконується (x, x)Ï RC, то (x, y)Ï RC для всіх y Î A;
(г) коли відповідність C є відображенням, то відношення RC транзитивне;
(д) коли відповідність C є відображенням, то RC - еквівалентність на A.
50. Для відповідності C між A і B через QC позначимо відношення на множині A, яке означається таким чином: для x, y ÎPr1 C вважаємо (x, y)Î QC тоді і тільки тоді, коли | C (x)Ç C (y)| = 1.
Довести, що для довільного антирефлексивного й симетричного відношення R на множині A існує така відповідність C між A і деякою множиною B, що R = QC.
51. Нехай R 1 і R 2 - еквівалентності на множині A. Довести, що
(а) R 1° R 1= A 2 Û R 1= A 2; (б) R 1° R 2= A 2 Û R 2° R 1= A 2.
52. Довести, що множини
(а) { A, 
}; (б) { A Ç B, A \ B, B \ A, Ç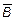 
}; (в) { A D B, A Ç B, 
}
є розбиттями універсальної множини E для довільних множин A, B Í E.
53. Побудувати всі можливі розбиття множини
(а) A = { a, b, c }; (б) A = {Æ,{Æ}}.
Відношення порядку
1. Довести, що множина всіх підмножин (булеан) даної множини є частково впорядкованою за відношенням включення Í.
2. Довести, що iA є частковий порядок на A.
3. Нехай a £ b Û a, b Î N і a ділить b. Довести, що £ - частковий порядок на N.
4. Означимо відношення R на множині цілих чисел Z таким чином: mRn тоді і тільки тоді, коли m - n є невід’ємним парним числом. Довести, що R - частковий порядок на Z. Чи є R лінійним порядком?
5. Означимо на множині R дійсних чисел відношення T: aTb тоді і тільки тоді, коли a /(a 2+1) £ b /(b 2+1), a,b Î R. Довести, що
(а) T не є відношенням часткового порядку на всій множині R;
(б) T є відношенням часткового порядку на множині дійсних чисел з інтервалу [1;¥);
(в) T є відношенням часткового порядку на множині дійсних чисел з інтервалу (-¥;-1].
6. Побудувати всі відношення часткового порядку на множині
(а) M = { a, b }; (б) M = { a, b, c }; (в) M = { a, b, c, d }.
7. Нехай M - скінченна множина і частковим порядком R на множині b(M) є відношення включення Í. Визначити величину | R | для заданої множини M.
(а) M ={1,2}; (б) M ={1,2,3}; (в) M ={1,2,3,4}; (г) M ={1,2,..., n }.
8. Нехай M ={1,2,3,4}. На множині b(M) задамо відношення R таким чином: (A, B)Î R тоді і тільки тоді, коли жодна з множин A і B не є підмножиною іншої. З’ясувати, чи є відношення R частковим порядком. Визначити величину | R |.
9. Довести, що якщо для елементів частково впорядкованої множини M виконується x 1£ x 2£...£ xn £ x 1, то x 1= x 2=...= xn.
10. Нехай M - довільна множина. Означимо відношення R на множині b (M)´ b (M): (A, B) R (C, D) тоді і тільки тоді, коли A D B Í C D D, A, B, C, D Î b (M). Чи є відношення R відношенням часткового порядку?
11. Нехай £ A частковий порядок на множині A, £ B - частковий порядок на множині B. Назвемо прямим добутком частково впорядкованих множин A і B множину A ´ B із заданим на ній відношенням £: (a 1 ,b 1)£(a 2 ,b 2) Û a 1£ Aa 2 і b 1£ Bb 2. Довести, що £ є частковим порядком на A ´ B;
12. Довести або спростувати таке твердження: якщо £ A лінійний порядок на множині A, а £ B - лінійний порядок на множині B, то відношення £, означене в попередній задачі, є лінійним порядком на множині A ´ B.
13. Довести, що для ланцюгів A і B прямий добуток A ´ B є ланцюгом лише тоді, коли або½ A ½= 1, або½ B ½=1.
14. Задамо відношення Q на множині Rn кортежів дійсних чисел довжини n таким чином: (a 1, a 2,..., an) Q (b 1, b 2,..., bn) тоді і тільки тоді, коли a 1£ b 1, a 2£ b 2,..., an £ bn. Довести, що Q є частковим порядком на Rn.
15. Нехай M - довільна множина. Означимо відношення R на множині b (M)´ b (M): (A, B) R (C, D) тоді і тільки тоді, коли A Í C і B Í D, A, B, C, D Î b (M). Визначити, чи є відношення R
(а) відношенням часткового порядку?
(б) відношенням лінійного порядку?
16. Нехай M - непорожня множина і P - множина всіх часткових порядків на M. Для R 1, R 2Î P покладемо R 1£ R 2 тоді і тільки тоді, коли з (a, b)Î R 1 випливає (a, b)Î R 2 для a, b Î M.
Довести, що означене відношення £ є частковим порядком на P.
17. Означимо відношення R на множині N 2: (a, b) R (c, d) тоді і тільки тоді, коли a £ c і b ³ d. Чи є відношення R відношенням часткового порядку?
18. На множині всіх підмножин (булеані) b (M) деякої множини M означимо відношення R: (A, B)Î R тоді і тільки тоді, коли існує бієкція між множинами A і B, A, B Î b (M). Чи буде відношення R відношенням часткового порядку на b (M)?
19. Означимо відношення R на множині N 2 : (a, b) R (c, d) тоді і тільки тоді, коли числа a і b та c і d є попарно взаємно простими і виконується a×d £ b×c. Довести, що відношення R є відношенням лінійного порядку на N 2.
20. Розташувати у лексикографічному порядку елементи множини:
(а) B 3, де B ={0,1}; (б) A 3, де A ={ a, b, c }.
21. Довести, що лексикографічний порядок є лінійним порядком на множині A * всіх слів в алфавіті A.
22. Підмножина B лінійно впорядкованої множини A з відношенням порядку £ називається щільною в A, якщо для будь-яких a, b Î A існує елемент c Î B такий, що a £ c £ b або b £ c £ a.
Чи є щільними у множині дійсних чисел R
(а) множина натуральних чисел N;
(б) множина цілих чисел Z;
(в) множина раціональних чисел Q;
(г) множина алгебраїчних чисел?
23. Довести, що R - частковий порядок тоді і тільки тоді, коли R- 1 частковий порядок.
24. Нехай { Ri } i Î I - система часткових порядків на множині A. Довести, що 
Ri - частковий порядок на множині A.
25. Нехай R - транзитивне відношення на множині M. Довести, що R є частковим порядком на M тоді і тільки тоді, коли R Ç R- 1 = iM.
26. Нехай R 1 і R 2 - часткові порядки на множині A. Чи буде частковим порядком R 1È R 2?
27. Нехай R 1 і R 2 - часткові порядки на множині A. Чи буде частковим порядком R 1° R 2?
28. Нехай R 1 і R 2 - лінійні порядки на множині A. Коли R 1° R 2 буде лінійним порядком на множині A?
29. Довести, що композиція R 1° R 2 відношень строгого порядку R 1 і R 2 буде строгим порядком, коли R 1° R 2 = R 2° R 1 і R 1Ç R 2 - 1 = Æ.
30. Нехай R - частковий (лінійний, повний) порядок на множині A, B - довільна підмножина множини A і R 1 - довільна підмножина R. Чи буде відношенням часткового (лінійного, повного) порядку
(а) R на множині B; (б) R 1 на множині A; (в) R 1 на множині B?
31. Нехай R - частковий (лінійний, повний) порядок на множині A і B Í A (B ¹Æ). Довести, що R Ç B 2 є частковий (лінійний, повний) порядок на множині B.
32. Нехай R - частковий порядок на множині A, який не є лінійним порядком, і B - непорожня підмножина множини A. Чи правильним є твердження, що відношення R Ç B 2 є частковим порядком на множині B, який не є лінійним?
33. Довести, що відношення часткового порядку R на множині M буде лінійним порядком тоді і тільки тоді, коли R È R -1 = M 2.
34. Довести, що об’єднання R 1È R 2 відношень часткового порядку R 1 і R 2 на множині M буде частковим порядком на множині M тоді і тільки тоді, коли R 1° R 2È R 2° R 1 Í R 1È R 2 і R 1Ç R 2-1 = iM.
35. Нехай R 1 - відношення еквівалентність, R 2 відношення строгого порядку. Довести, що відношення R 1° R 2° R 1 буде строгим порядком тоді і тільки тоді, коли R 2° R 1° R 2Í R 1° R 2° R 1 і R 1Ç R 2 = Æ.
36. Довести, що об’єднання R 1È R 2 відношень строгого порядку R 1 і R 2 буде строгим порядком тоді і тільки тоді, коли R 1° R 2È R 2° R 1Í R 1È R 2.
37. Довести, що відношення R на множині A є одночасно відношенням еквівалентності та частковим порядком тоді і тільки тоді, коли R = iA.
38. Нехай £ - частковий порядок на множині A. Означимо відношення < на частково впорядкованій множині A: a < b тоді і тільки тоді, коли a £ b і a ¹ b. Довести, що відношення < іррефлексивне та транзитивне.
39. Довести, що коли деяке відношення < на A іррефлексивне та транзитивне, тоді відношення x £ y Û (x < y або x = y) є частковим порядком на A.
40. Довести, що для довільної частково впорядкованої множини M з k елементів існує таке відображення f: M ® Nk, що для елементів ai, aj Î M зі співвідношення ai < aj випливає нерівність f (ai)< f (aj).
41. Довести, що транзитивне замикання R * відношення часткового порядку R збігається з R, тобто R * = R.
42. Довести, що транзитивне замикання R * рефлексивного відношення R на множині M буде відношенням часткового порядку на M тоді і тільки тоді, коли R * антисиметричне. Сформулюйте цю умову в термінах відношення R.
43. Нехай £ і < - це традиційні відношення порядку на множині натуральних чисел N. Довести, що
(а) < ° < ¹ <; (б) £ ° < = <; (в) £ ° ³ = N 2.
44. На множині N 2000 означено частковий порядок R за допомогою відношення «ділить», тобто mRn тоді і тільки тоді, коли m ділить n. Чи існують у множині N 2000 найменший і найбільший елементи? Чи є в множині N 2000 мінімальні й максимальні елементи, і якщо є, то визначити їхню кількість. Узагальнити відповідь на випадок множини Nk для довільного k Î N.
45. Визначити для скількох відношень часткового порядку на множині M елемент a буде мінімальним.
(а) M ={ a, b }; (б) M ={ a, b, c }; (в) M ={ a, b, c, d }.
46. Довести, що будь-яка частково впорядкована множина містить не більше одного найбільшого (найменшого) елемента.
47. Довести, що найбільший (найменший) елемент частково впорядкованої множини є єдиним максимальним (мінімальним) елементом у цій множині.
48. Побудувати приклад частково впорядкованої множини, яка має
(а) точно один мінімальний елемент, але не має найменшого елемента;
(б) точно один максимальний елемент, але не має найбільшого елемента;
(в) один мінімальний і один максимальний елементи, але не має найменшого й найбільшого елементів;
(г) не має жодного мінімального і максимального елементів та не має найменшого й найбільшого елементів.
49. Довести, що будь-яка непорожня скінченна частково впорядкована множина A містить мінімальний і максимальний елементи.
50. Довести, що скінченна частково впорядкована множина має найменший (найбільший) елемент тоді і тільки тоді, коли вона містить рівно один мінімальний (максимальний) елемент. Чи справедливо це для нескінченних частково впорядкованих множин?
51. Нехай частково впорядкована множина A є скінченною. Довести, що для будь-якого елемента a Î A існують елементи b і c з A такі, що
(а) a £ b і b є максимальним елементом у множині A;
(б) c £ a і c є мінімальним елементом у множині A.
52. Скільки одиничок містить матриця C відношення лінійного порядку R на скінченній множині M з n елементів?
53. Нехай C - матриця відношення часткового порядку R на скінченній множині M з n елементів. Як за допомогою матриці C можна визначити існування в множині M
(а) мінімальних елементів; (в) найменшого елемента;
(б) максимальних елементів; (г) найбільшого елемента.
55. Побудувати лінійний порядок на множині:
(а) N 2; (б) N È N 2È N 3È...È Nn È...; (в) C комплексних чисел.
56. Довести, що множина N натуральних чисел з традиційним відношенням порядку є цілком упорядкованою.
57. Довести, що
(а) множина N, де 0<2<4<...<1<3<5... є цілком упорядкованою;
(б) множина N, де...4<3<2<1 не є цілком упорядкованою.
(в) множина Z, де 1<2<3<...<0<-1<-2<-3<... є цілком упорядкованою.
58. Довести, що множина Z цілих чисел з традиційним відношенням порядку не є цілком упорядкованою.
59. Довести, що будь-яка скінченна лінійно впорядкована множина є цілком упорядкованою.
60. Чи будуть цілком упорядкованими такі множини:
(а) множина Q раціональних чисел з традиційним відношенням порядку;
(б) множина R дійсних чисел з традиційним відношенням порядку;
(в) множина чисел виду 1-1/ n, де n Î N з традиційним відношенням порядку.
61. Довести, що будь-яка підмножина цілком упорядкованої множини є цілком упорядкованою.
62. Знайти всі множини M, для яких існує повний порядок R на M такий, що R -1 також є повним порядком на M.
63. Довести, що будь-яка непорожня цілком упорядкована множина має найменший елемент.
