Процедура топологічної декомпозиції структури системи полягає у представлені її орієнтованим графом з виділенням окремих сильно зв’язаних підграфів, які задаватимуть структури підсистем.
З метою визначення рівнів ієрархії у структурі, упорядкування по рівнях її елементів будують порядкові функції. Таке упорядкування також необхідне для введення загальних правил нумерації вершин.
В множину нульового рівня 
включають всі елементи структури, для яких 
Æ.
В множину першого рівня 
включають всі елементи, для яких 
.
Множина n -го рівня 
включає усі елементи для яких: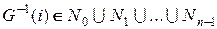 
.
Після розміщення елементів по рівнях проводиться їх наскрізна нумерація в такий спосіб, щоб вершина, яка входить в множину нижнього рівня мала менший номер ніж вершина, яка входить у множину вищого рівня.
Для оцінки кількісних агрегованих характеристик системи на основі аналізу структури, кожному зв’язку чи елементу ставиться у відповідність деяке числове значення 
, 
. Побудова числових функцій, які задаватимуть агреговані характеристики на структурі, переважно пов’язана із знаходженням максимального чи мінімального шляху. Числові функції можуть мати адитивний характер 
, чи мультиплікативний 
.
Задача знаходження максимального або мінімального шляху на структурі є задачею динамічного програмування.
Можливості структури розкриваються при відображені її структурно- топологічних характеристик, серед яких слід відзначити: зв’язаність, надлишковість, рівномірність розподілу зв’язків, компактність.
Зв’язаність структури – це кількісна характеристика, яка дозволяє виявити розриви у структурі, ізольовані елементи. Для її оцінки будують матрицю зв’язаності:
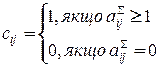
Елементи 
належать матриці 
, яка розраховується за формулою:
, де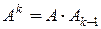 
Якщо структура представляється неорієнтованим графом, то структурна зв’язаність відповідає умові: 
Надлишковість структури – це показник, який показує відношення загальної кількості зв’язків до мінімально необхідної для забезпечення повної зв’язаності. У випадку представлення структури неорієнтованим графом, і відображенням його матрицею суміжності, цей показник матиме вигляд
Рівномірність розподілу зв’язків 
характеризує повноту використання можливостей структури з 
зв’язків та 
вершин, при досягненні максимальної зв’язаності. Для його розрахунку на основі представлення неорієнтованим графом вводять поняття ступені вершини 
– кількості зв’язків які інцидентні (входять чи виходять з вершини). Тоді розраховують середню ступінь вершини 
та середньо квадратичне відхилення
Компактність структури визначається наближеністю елементів між собою, що у подальшому аналізі дозволить прогнозувати інерційність системи з заданою структурою. Наближеність елементів один до одного будемо визначати мінімальною відстанню між ними 
, якщо числові функції неможливо встановити на цьому етапі аналізу структури, то відстань між елементами визначаю кількістю проміжних зв’язків між ними, а агрегований показник компактності структури визначають за одною із таких формул:
– абсолютний показник;
– відносний показник,
де 
;
– діаметр структури.
