Этот вид работы с большим трудом усваивается учащимися школы VIII вида. Одна из трудностей состоит в том, что ученики с трудом понимают, каким образом одна и та же величина может иметь различную числовую характеристику, т. е., например, как может быть, что длина класса 7 м, 70 дм, 700 см. Числа разные, но они характеризуют одну и ту же величину — длину класса.
Другая трудность возникает при выполнении преобразований: 5 р. = 500 к., 200 см=2 м (название более крупной меры ставится рядом с меньшим числом).
При выполнении преобразований, как показывают опыт и специально проведенные исследования, учащиеся чаще всего допускают такие ошибки:
1)при замене крупных мер мелкими: 4 км 85 м=485 м (пропущен
нуль); 78 м 5 дм = 7805 дм (вставлен лишний нуль);
35 р. 7 к.=3570 к. (нуль стоит не на месте); 35 км 386 м=35 386 км;
3 кг 85 г=3085 км (неверно записано наименование); 4 р. 70 к.=470
(результат не имеет наименования);
2)при замене мелких мер крупными: 28 746 к.=28 р. 746 к.;
8050 г=80 кг 50 г или 805 кг 0 г (неумение вычленить из числа
нужные разряды); 387 м=3 кг 87 м, 2308 кг=2 р. 308 к.=23 р.
08 к. (неправильная запись наименований); 785 ц=7 кг 85 ц
(нарушение порядка наименований); 280 кмх2=5600 кв. м=5(> и (случайная запись наименований).
Одной из причин взаимозаменяемости наименований этих мер является отрыв их от конкретного образа, а также сходство и звучании.
Поэтому полезны такие задания: отмерить полоску длиной 10 см, а затем определить длину этой же полоски в дециметрах, Значит, длина этой полоски равна 1 дм, или 10 см, т. е. в этом случае происходит замена крупных мер более мелкими. Наоборот, можно записать, что длина полоски равна 10 см, или 1 дм, т. е произвести замену мелких мер более крупными.
Надо найти длину карандаша в сантиметрах (14 см), а потом в дециметрах и сантиметрах (1 дм 4 см). 14 см содержит 1 десяток сантиметров, или 1 дм и еще 4 см. Опираясь на равенство отрезков, записываем: 14 см=1 дм 4 см, а 1 дм 4 см=14 см, т. е. мелкие меры заменили крупными, а крупные — мелкими.
Также путем сравнения отрезков учеников обучают замене миллиметров сантиметрами и наоборот. Например, предлагается найти длину гвоздя в сантиметрах, а получившийся остаток (меньше сантиметра) в миллиметрах. Получаются два числа: 1 см 5 мм и 15 мм, которые характеризуют одну и ту же величину. Значит, 1 см 5 мм=15 мм. Полезно давать задания и такого типа: найти величину (длину) двумя единицами измерения, а затем одной и сравнить результаты.
Чтобы выполнить эти преобразования, учащиеся должны уметь умножать 10, 100, 1000, а также делить на 10, 100, 1000 как без остатка, так и с остатком (соотношение мер, изучаемых во вспомогательной школе, связано с числами 10, 100, 1000); уметь привести примеры чисел, полученных при измерении величин с соотношением единиц, равным либо 10, либо 100, либо 1000, например: 3 см 5 мм, 8р. 15 к., 3 км 859 м и т. д.
Последовательность изучения преобразований чисел, полученных от измерения величин, связана с последовательностью изучения нумерации целых неотрицательных чисел и действий над ними.
Знакомство с преобразованием чисел начинается с замены крупных мер мелкими (5-й класс). Прежде всего надо создать такую ситуацию, в которой учащиеся могли бы убедиться в необходимости этого преобразования.
Например, ученику предлагается измерить полоску в децимет-||.|.\; отрезать от нее полоску длиной в 4 см и ответить на вопро-и,1. какой длины полоска осталась? Какой длины полоска была? (I дм.) Сколько сантиметров отрезали? (4 см.) Запись дается икая: 1 дм — 4 см. Надо 1 дм заменить 10 см.
Далее проводятся специальные упражнения, например:
5 р. =... к.
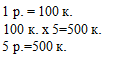2 дм=... см
1 дм=10 см
10 смх2=20 см
2 дм=20 см
В приведенных примерах крупные меры заменялись (выражались) мелкими.
Параллельно с этим преобразованием учитель показывает, как число, полученное от измерения в мелких мерах, выразить в крупных мерах.
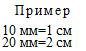Объяснение
1 десяток миллиметров составляет 1 см. Сколько десятков в числе 20? В числе 20 содержится 2 десятка (20:10=2). Значит, 20 мм — это 2 см.
На данном этапе полезно провести сопоставление с разрядными единицами:
100 ед. = 1 сот. 100 к. = 1 р. 200 ед.=2 сот. 200 к.=2 р. 800 ед.=8 сот. 800 к.=8 р.
Чтобы узнать, сколько рублей содержится в данном числе, надо число копеек разделить по 100 к.
Далее рассматриваются более трудные случаи. Например, надо 5 см 6 мм выразить в миллиметрах. Так как в 1 см содержится 10 мм, то 5 см будет в 5 раз больше. 10 мм-5=50 мм, затем 50 мм+6 мм=56 мм, значит, 5 см 6 мм=56 мм.
Обратная задача: выразить число в более крупных единицах измерения, например 56 мм надо выразить в сантиметрах и миллиметрах. Вспомним, что 10 мм=1 см. Далее учитель спрашивает: «Сколько десятков в числе 56?» (В числе 56 содержится 5 десятков, или 5 см. Значит. 56 мм=5 см 6 мм.)
 |
Особое внимание следует обратить на запись чисел, получен! от измерения, с пропущенными разрядами, например таких: 3 р. ' В связи с этим примером необходимо вспомнить, что в 1 р. содерж; ся 100 к., в 3 р. — 300 к. в результате устанавливается, что в чи< 3 р. 7 к. пропущен разряд десятков (7 к. — это единицы) и вме> пропущенного разряда следует вписывать нуль: 3 р. 07 к. Такая пись предотвратит возможные, часто встречающиеся оши(н (3 р. 7 к.=37 к.) при замене крупных мер мелкими и при выполнении действий (3 р. 7 к.+4 р. 8 к.=8 р. 5 к.).
Следует сопоставить запись многозначных чисел и чисел, полу ченных от измерения величин такого вида: 3 р. 07 к. и 30/. 5 кг 056 г и 5056, 8 т 005 кг и 8005, 10 250 и 10 тыс. 250 ел. 10 250 м и 10 км 250 м.
Полезны такие задания:
Сколько всего единиц тысяч в числе 27 245?
Вставь пропущенные числа: 45 ед. =... дес.... ед., 45 см = =... дм... см.
Замени мелкие меры крупными: 475 к. =... р.... к. 3745 к. =..., 185 см =..., 3075 г=...
Вставь пропущенные числа: 10 м 45 см=... см, 3 т 405 кг=... кг. Сравни числа (вставь знаки >, <, =): 4500 м... 4 км 50 м, 7 т 5 ц... 7 т 500 кг, 3800 к.... 380 р.
Поставь нужные наименования: 1... =1000..., 1... = 100....
