ИЗМЕРЕНИЯ. ОЦЕНКА ПОГРЕШНОСТЕЙ
В основе точных естественных наук, к числу которых относится и физика, лежат измерения. Измерения - это процедура, которая ставит в соответствие физической величине некоторое число. Мы говорим, что физическая величина А измерена, если известно сколько раз в А содержится некоторая единица а. Это и есть числовое значение а величины А. Само по себе число а не несет никакой информации. Указывая число а, необходимо указать и единицу измерения а. Тогда можно записать А =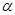 
а. Например, если масса т тела в пять раз больше 1кг, значит т = 5 кг.
Полученные в результате измерений значения различных величин могут зависеть друг от друга. Физика устанавливает связь между такими величинами и выражает ее в виде формул, которые показывают, как числовые значения одних величин могут быть найдены по числовым значениям других.
Измерения делятся на прямые и косвенные. Прямые измерения проводят с помощью приборов, которые измеряют саму исследуемую величину. Так, массу тел можно найти с помощью весов, длину измерить линейкой, а время - секундомером. Те же величины в других случаях могут быть найдены только с помощью косвенных измерений - пересчетом других величин, значения которых получены в результате прямых измерений. Так находят массуЗемли, расстояние от Земли до Солнца, продолжительность геологических периодов. Измерение плотности тел по их массе и объему, скорости поезда - по величине пути, пройденного за известное время, также принадлежат к косвенным измерениям.
Получение надежных числовых значений физических величин отнюдь не является простой задачей из-за многочисленных погрешностей, неизбежно возникающих при измерениях. Ниже мы отметим эти погрешности и приведем формулы для их оценки, а также обратим внимание на запись окончательного результата измерений.
Случайные и систематические погрешности. Обработка результатов прямых измерений. Запись окончательного результата
Говоря о погрешностях измерений, следует, прежде всего, упомянуть о грубых погрешностях (промах), возникающих вследствие недосмотра экспериментатора или неисправности аппаратуры. Такие погрешности происходят, если, например, экспериментатор неправильно прочтет номер деления на шкале, если в электрической цепи произойдет замыкание и вследствие других подобных причин. Грубых погрешностей следует избегать. Если установлено, что они имеют место, соответствующие измерения нужно отбрасывать.
Не связанные с вышеупомянутыми погрешности эксперимента делятся на случайные и систематические. Многократно повторяя одни и те же измерения, можно заметить, что довольно часто их результаты не в точности равны друг другу, а "пляшут" вокруг некоторого среднего. В подобных случаях мы имеем дело со случайными погрешностями.
Случайные погрешности могут быть связаны с сухим трением (из-за которого стрелка прибора вместо того, чтобы останавливаться в правильном положении, "застревает" вблизи него), с люфтами в механических приспособлениях, с тряской, которую в городских условиях трудно исключить, с несовершенством объекта измерений (например, при измерении диаметра проволочки, которая из-за случайных причин, возникающих при ее изготовлении, имеет не вполне круглое сечение). Рассмотрим последний случай.
Пусть измерения диаметра проволочки в различных ее местах, полученные при помощи микрометра, имеют следующие результаты:
| № опыта | |||||||
| диаметр (мм) | 0,36 | 0,36 | 0,35 | 0,34 | 0,36 | 0,34 | 0,35 |
Вместо одного нужного нам результата мы получили семь. Что делать с полученными цифрами? Как оценить погрешности?
В качестве наилучшего значения для измеренной физической величины Х обычно принимают среднее арифметическое из всех полученных результатов
. (1)
В нашем случае получим
.
Этому результату следует приписать случайную погрешность, определяемую формулой
. (2)
В нашем случае
.
Отсутствие случайной погрешности отнюдь не означает, что измерение проведено абсолютно точно, так как на ряду со случайными погрешностями имеют место систематические.
Систематические погрешности могут быть связаны с несовершенством методики эксперимента (например, пренебрегая силами трения при колебании маятника, мы уже допускаем неточность), с ошибками приборов (неправильная шкала, неравномерно растягивающаяся пружина, неравномерный шаг микрометрического винта и т.д.).
Систематические погрешности сохраняют свои значения во время эксперимента.
Оценку систематической погрешности 
экспериментатор проводит, анализируя особенности методики эксперимента, паспортную точность приборов и делая контрольные опыты.
В дальнейшем в качестве систематической погрешности мы будем брать приборную погрешность, которая, как правило, равна половине цены деления шкалы измерительного прибора.
В рассматриваемом примере с проволочкой цена деления шкалы микрометра 
= 0.01 мм. Следовательно,
= 
= 0.005 мм.
Полная погрешность определения физической величины 
находится через случайную 
и систематическую погрешности по формуле
= 
.
В нашем случае имеем:
Как записать теперь окончательный результат измерений?
Пусть в результате расчетов по формулам (1), (2) и (3) для 
и получены следующие значения:
= 1.992205 (ед. измерения)
= 0.003691 (ед. измерения)
Окончательный результат измерения физической величины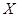 
записывается в виде
. (4)
Имейте в виду, что преждечем подставлять в формулу (4) численные значения и , необходимо провести округления.
Значение погрешности округляются до двух значащих цифр, если первая из них является единицей, и до одной значащей цифры во всех остальных случаях. С учетом этого = 0,004 (ед. измерения). Анализируя значение погрешности, можно сделать вывод, что значение должно быть округлено до третьей цифры после запятой, т.е.
= 1.992 (ед. измерений).
Таким образом, окончательным результатом измерения является:
Х = 1.992 ± 0.004 (ед. измерений).
В рассматриваемом примере с изменением диаметра проволочки можно записать
d = (0.350 ± 0.006) мм.
Обработка результатов косвенных измерений
Пусть интересующая нас физическая величина X связана с величинами a и b некоторым физическим соотношением
Х= 
,
причем величины a и b определены в результате прямых измерений, т.е. нам известны 
Результат косвенного измерения величины Х записывается в виде
где в качестве наилучшего значения для Х принимается
(5)
а погрешность 
рассчитывается через погрешности 
и 
поформуле
(6)
где 
и 
- частные производные функции f по переменным а и b.
Применение формулы (6) для конкретных функций 
приводит к следующим формулам для оценки погрешностей:
: 
;
: 
;
: 
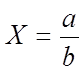; (7)
Рассмотрим следующий пример. Предположим, что Вы хотите определить ускорение свободного падения g. Пренебрегая сопротивлением воздуха для свободно падающего стального шарика, можно записать:
,
где t - время падения, а h - высота, с которой падает шарик. Таким образом, измеряя высоту h и время падения t, можно рассчитать ускорение свободного g падения по формуле
.
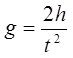Вы пять раз сбрасываете шарик с одной и той же высоты и измеряете время t. Пусть результаты измерений времени следующие:
с;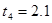 
с; 
с; 
с; 
с.
Измерение времени проводится секундомером, цена деления шкалы которого
с.
Измеряя высоту h, получили 
м.
Обработаем результаты измерений в соответствии с формулами (1),(2),(3),(5),(7) и определим ускорение свободного падения:
Таким образом, в рассмотренном эксперименте результатом измерения свободного падения является 
