Уравнение называется линейным, если неизвестные величины входят в него только в первой степени и с постоянными коэффициентами. Система линейных алгебраических уравнений может быть записана в следующем виде:
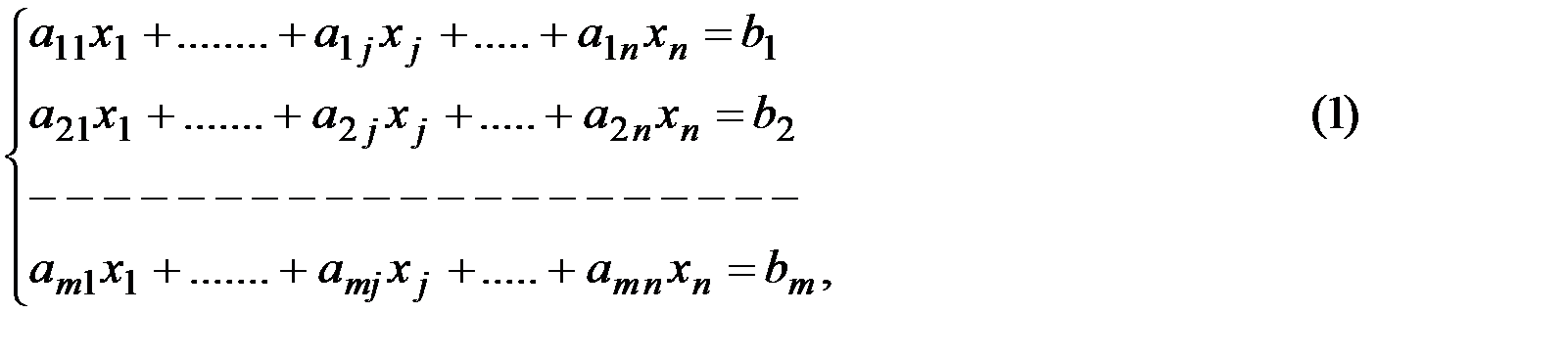
где 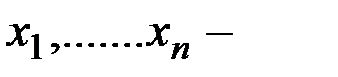 переменные, а
переменные, а  и
и 
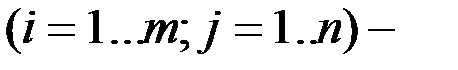 известные числа.
известные числа.
Среди различных методов решения системы (1) наиболее эффективным и важным для дальнейшего является метод Жордана−Гаусса.
Решение системы линейных алгебраических уравнений методом Жордана−Гаусса заключается в последовательном исключении переменных при помощи тождественных преобразований, приводящих систему к эквивалентной ей системе с базисом.
Система линейных алгебраических уравнений называется системой с базисом, если в каждом ее уравнении имеется неизвестное, входящее в данное уравнение с коэффициентом, равным единице, и не входящее ни в одно из остальных уравнений. Если предположить, что в  -м уравнении выделенной служит неизвестная
-м уравнении выделенной служит неизвестная 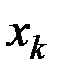 , то систему с базисом можно записать в виде:
, то систему с базисом можно записать в виде:
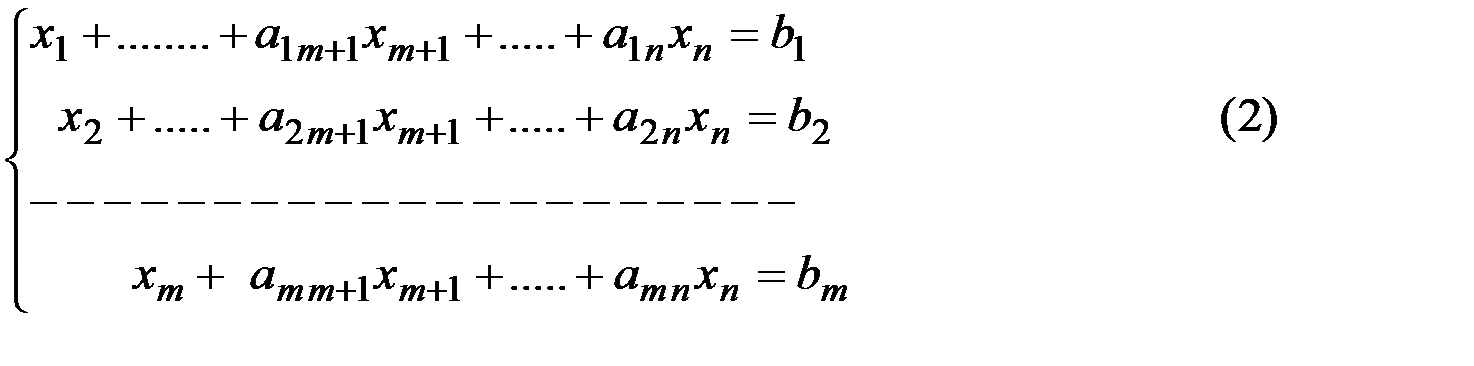
Неизвестные 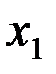 ,
,  ,……
,……  называют базисными, а остальные
называют базисными, а остальные 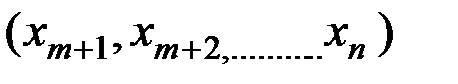 - свободными. Если члены, содержащие свободные неизвестные, перенести в правые части уравнений, то система
- свободными. Если члены, содержащие свободные неизвестные, перенести в правые части уравнений, то система  запишется в следующей форме:
запишется в следующей форме:

Соотношения (3) дают общее решение системы (2): свободные переменные могут принимать произвольные значения, а значения базисных переменных определяются системой (3).
Если все свободные переменные положить равными нулю, то базисные переменные будут равны правым частям уравнениям. Такое решение называют базисным.
Для получения решения системы линейных алгебраических уравнений достаточно привести эту систему к виду системы с базисом, то есть в каждом уравнении выделить базисную переменную.
Весь алгоритм метода Жордана−Гаусса оформляется в виде последовательных таблиц, отражающих выполняемые преобразования системы. Каждая строка таблицы соответствует одному из уравнений. В первом столбце записывают правые части уравнений, в остальных - коэффициенты при неизвестных.
Приведем основные правила метода Жордана−Гаусса и затем проиллюстрируем его применение на конкретном примере.
Каждый шаг преобразований по методу Жордана−Гаусса требует выполнения следующих действий:
1. Выбор ключевого (главного) элемента.
За ключевой элемент строки можно принять любой отличный от нуля коэффициент при одном из неизвестных. Строку и столбец ключевого элемента называют ключевыми.
2. Преобразование ключевой строки.
Все элементы ключевой строки делятся на ключевой элемент, при этом на месте ключевого элемента появляется единица. Ключевую строку помечают, например, символом * слева от таблицы. Это позволяет в дальнейшем контролировать количество уже преобразованных ключевых строк.
3. Назначение дополнительных множителей.
Каждой неключевой строке исходной таблицы ставится в соответствие множитель, равный взятому с обратным знаком ее элементу, стоящему в ключевом столбце. Эти множители приписывают справа от таблицы.
4. Преобразование неключевых строк.
Для преобразования неключевой строки нужно каждый элемент преобразованной ключевой строки умножить на дополнительный множитель преобразуемой строки и сложить с соответствующим элементом неключевой строки.
5. Появление нулевой строки.
Если в ходе вычислений появляется строка, состоящая из одних нулей, то такая строка вычеркивается из таблицы, поскольку соответствующее ей уравнение является следствием остальных уравнений системы.
6. Окончание преобразования таблицы. Преобразование строк таблицы продолжается до тех пор, пока не останется непомеченных строк. При этом возможны три случая:
а) количество меток равно количеству переменных; в этом случае решение задачи единственно и ключевые переменные равны правым частям последней таблицы.
б) количество меток меньше количества переменных; в этом случае существует бесконечное число решений задачи; ключевые переменные при этом выражаются через остальные, т.е. свободные переменные, которые могут принимать произвольные значения.
в) в ходе преобразования строк появляется противоречивая строка, в которой все коэффициенты при неизвестных равны нулю, а свободный член отличен от нуля; в этом случае система не имеет решений, поскольку соответствующее уравнение системы не выполняется ни при каких значениях переменных.
Пример. Решить систему уравнений методом Жордана-Гаусса.

Решение. Занесем коэффициенты системы в таблицу согласно описанным выше правилам (см. Табл.1).
В Таблице 1 приведены промежуточные таблицы Т.1-Т.4, соответствующие последовательным этапам решения данной задачи.
В Т.1-Т.4 звездочками отмечены строки, в которых уже был выбран ключевой элемент. В Т.4 появляется строка, в которой все коэффициенты при неизвестных равны нулю. Эта строка исключается, после чего уже в каждой строке таблицы имеется ключевой элемент.
Таблица 1

| 
| 
| 
| 
| 
| Дополн.множ. | ||
| Т.1 | -4 | -5 | -2 | -- | ||||
| -1 | -1 | -2 | ||||||
| -9 | -6 | -4 | -3 | -3 | ||||
| -8 | -6 | -7 | ||||||
| * | -4 | -5 | -2 | |||||
| Т.2 | -- | |||||||
| -2 | -6 | -2 | ||||||
| -8 | ||||||||
| * | 28/3 | 13/3 | -1 | |||||
| * | 20/3 | 5/3 | -3 | |||||
| Т.3 | -31/3 | -4 | -28/3 | -- | ||||
| -31/3 | -4 | -28/3 | -3 | |||||
| * | 115/9 | 13/3 | 67/9 | |||||
| * | ||||||||
| * | -31/9 | -4/3 | -28/9 | |||||
| Т.4 |
Таблица Т.4 дает запись системы с базисом, эквивалентной исходной:

Общее решение этой системы, а значит и исходной, дается формулами:

Положив свободные переменные равными нулю  , получаем базисное решение
, получаем базисное решение  .
.
Чтобы убедиться в правильности полученного решения, следует сделать проверку. Для этого нужно подставить общее решение в исходные уравнения системы. Все уравнения должны при этом обратиться в тождества. Если этого не происходит, следует искать ошибку в вычислениях.
В нашем примере подстановка общего решения в уравнения системы (4) приводит к следующим соотношениям:


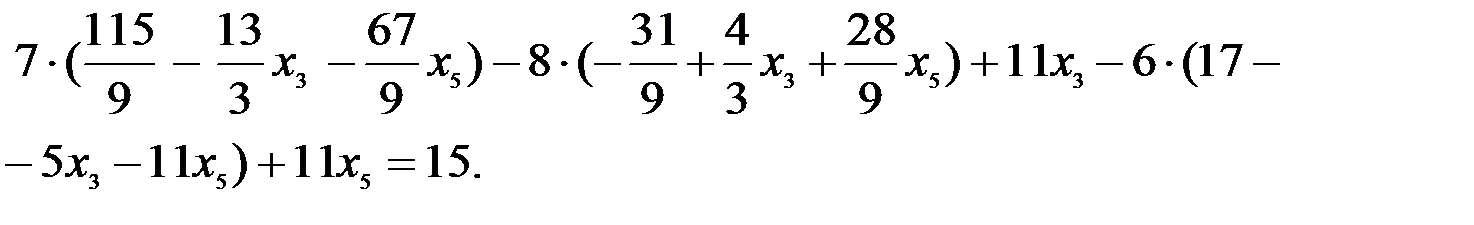
Нетрудно убедиться, что все уравнения превращаются в тождества. Следовательно, задача решена верно.
Если бы в условиях рассмотренного примера правая часть последнего уравнения системы (4) была равна числу, отличному от 15, в таблице Т.4 вместо нулевой появилась бы противоречивая строка и система не имела бы решений.
Контрольные задания
2.1-2.20. Решить систему методом Жордана-Гаусса. Найти общее решение и два частных решения. Сделать проверку.
2.1. 2.2.


2.3. 2.4.


2.5. 2.6.


2.7. 2.8.
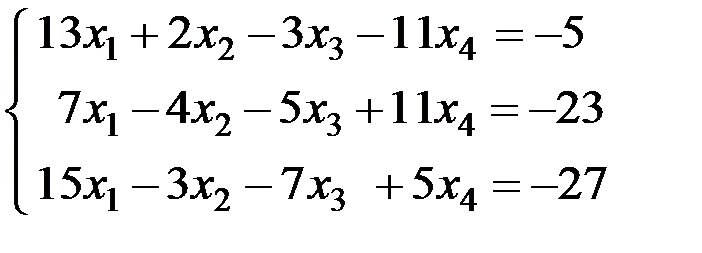
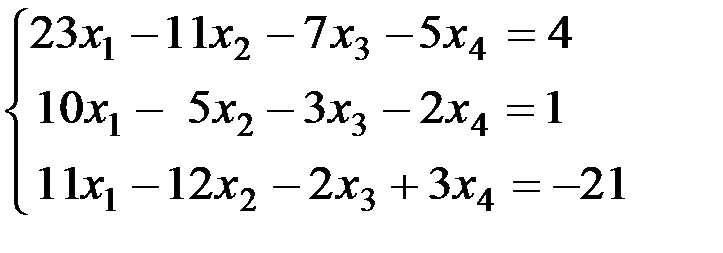
2.9. 2.10.


2.11. 2.12.


2.13. 2.14.


2.15. 2.16.


2.17. 2.18.


2.19. 2.20.


ТЕМА 3. ПРЕДЕЛ ФУНКЦИИ
Число А называется пределом функции y = f (x) при х, стремящемся к бесконечности, если для любого сколь угодно малого положительного числа ε > 0 найдется такое положительное число S > 0 (зависящее от ε: S = S (ε)), что для всех х таких, что | x | > S, верно неравенство
| f (x) – A | < ε.
Этот предел функции обозначается
 или f (x) → А при х → ∞.
или f (x) → А при х → ∞.
Число А называется пределом функции y = f (x) при х, стремящемся к х 0,если для любого сколь угодно малого положительного числа ε > 0 найдется такое положительное число δ > 0 (зависящее от ε: δ = δ(ε)), что для всех х, не равных х 0 и удовлетворяющих условию | x – x 0| < δ, выполняется неравенство
| f (x) – A | < ε.
Этот предел функции обозначается
 или f (x) → А при х → х 0.
или f (x) → А при х → х 0.
Если при стремлении х к х 0 переменная х принимает лишь значения, меньшие х 0, или, наоборот, лишь значения, большие х 0, и при этом функция f (x) стремится к некоторому числу А, то говорят об односторонних пределах функции f (x), левостороннем и правостороннем:


Функция α(х) называется бесконечно малой величиной (б.м.) при х → х 0 или при х → ∞, если ее предел равен нулю: 
Свойства бесконечно малых (б.м.) величин.
10. Алгебраическая сумма конечного числа б.м. величин есть б.м.
20. Произведение б.м. величины на ограниченную функцию (в том числе на постоянную, на другую б.м.) есть величина б.м.
30. Частное от деления б.м. величины на функцию, предел которой отличен от нуля, есть величина б.м.
Если

то б.м. величины α(х) и β(х) при х → х 0 (х → ∞) называются эквивалентными, и в этом случае пишут α(х) ~ β(х).
Можно показать что, если существует предел отношения двух б.м. величин, конечный или бесконечный, то он не изменится, если эти б.м. заменить им эквивалентными. Это означает, что эквивалентные б.м. величины взаимозаменяемы при вычислении пределов.
Примеры эквивалентных б.м.:
sin x ~ x; tg x ~ x; ℮ x – 1 ~ x; ln(1 + x) ~ x;
arcsin x ~ x; arctg x ~ x;
(1 + x) m ~ 1 + mx; 1 – cos x ~ x 2/2.
Функция f (x) называется бесконечно большой величиной (б.б.) при х → х 0, если для любого, даже сколь угодно большого положительного числа М > 0, найдется такое положительное число δ > 0 (зависящее от ε: δ = δ(ε)), что для всех х, не равных х 0 и удовлетворяющих условию | x – x 0| < δ, выполняется неравенство
| f (x)| > M.
Аналогично можно определить понятие бесконечно большой (б.б.) величины при х → ∞. Приведем его в краткой форме 
Свойства бесконечно больших величин.
10. Произведение б.б. величины на функцию, предел которой отличен от нуля, есть б.б. величина.
20. Сумма б.б. величины и ограниченной функции есть б.б. величина.
30. Частное от деления б.б. величины на функцию, имеющую предел, есть б.б. величина.
Теорема. Если функция α(х) есть б.м. величина при х → х 0 (х → ∞), то функция  является б.б. величиной при х → х 0 (х → ∞). И наоборот, если функция f (x) есть б.б. величина при х → х 0 (х → ∞), то функция
является б.б. величиной при х → х 0 (х → ∞). И наоборот, если функция f (x) есть б.б. величина при х → х 0 (х → ∞), то функция  есть б.м. величина при х → х 0 (х → ∞).
есть б.м. величина при х → х 0 (х → ∞).
Приведем основные теоремы о пределах.
1. Если предел существует, то он единственный.
2. Если функция y = f (x) в окрестности некоторой точки х 0 монотонно возрастает (убывает), то она в этой точке имеет предел. Причем, если к тому же функция y = f (x) ограничена сверху (снизу), то этот предел конечен.
3. 


В частности, постоянный множитель можно выносить за знак предела

4. 
5. Функция y = f (x), имеющая в точке х 0 конечный предел, ограничена.
Первым замечательным пределом называется предел

Вторым замечательным пределом (числом ℮) называется предел
 или
или  .
.
Пример 1. Найти предел  .
.
Решение. Очевидно, что числитель дроби 3 x 2 – 1 при x→2 стремится к 3∙22 – 1 = 11. Аналогично знаменатель стремится к 23 + 1 = 9. Тогда вся дробь будет стремится к  . Таким образом,
. Таким образом,  =
=  .
.
Пример 2. Найти предел  .
.
Решение. При х → 8 числитель (2х - 7) стремится к 2∙8 - 7 = 9, т. е. является ограниченной функцией, а знаменатель (х - 8) стремится к нулю, т. е. является б.м. величиной. Отсюда по свойствам б.м. величин искомый предел равен ∞.
Пример 3. Найти предел  .
.
Решение. Если подставить x = 1 в рассматриваемую функцию, получим ноль в числителе и знаменателе. Без дополнительных преобразований трудно сказать, к чему будет стремиться подобное выражение. Поэтому такие выражения называются неопределенностями. Встречаются неопределенности вида  ,
, 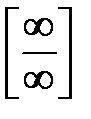 , [∞ - ∞], [0 ∙ ∞], [1∞], для каждой из которых существуют свои способы вычисления пределов, то есть раскрытия неопределенностей.
, [∞ - ∞], [0 ∙ ∞], [1∞], для каждой из которых существуют свои способы вычисления пределов, то есть раскрытия неопределенностей.
Теперь решим пример. Разложим числитель на множители
 =
=  =
=  = 7.
= 7.
Для решения задач, где ищется предел дробно-рациональной функции (отношения двух многочленов), можно пользоваться следующим правилом:
Пусть Р n = a 0 + a 1 x + a 2 x 2 + … + a n xn и Q m = b 0 + b 1 x + b 2 x 2 + … + b m xm. Тогда
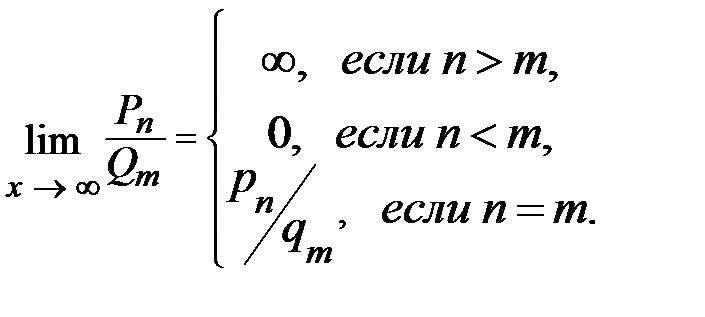
Пример 4. 1) Найти  . По указанному правилу, т.к. старшая степень числителя n =
. По указанному правилу, т.к. старшая степень числителя n =  , а старшая степень знаменателя m = 2, то предел равен ∞.
, а старшая степень знаменателя m = 2, то предел равен ∞.
2) Найти  . Старшая степень числителя n = 2, старшая степень знаменателя m = 3. Имеем n < m, поэтому предел равен 0.
. Старшая степень числителя n = 2, старшая степень знаменателя m = 3. Имеем n < m, поэтому предел равен 0.
3) Найти  . Старшая степень числителя n =
. Старшая степень числителя n =  = 1, старшая степень знаменателя m =
= 1, старшая степень знаменателя m =  = 1. Имеем n = m, поэтому предел равен
= 1. Имеем n = m, поэтому предел равен  =
=  .
.
Пример 5. Найти  .
.
Решение. Подставив в заданную функцию x = 1, получаем неопределенность вида  . Здесь мы воспользуемся известным фактом, что если некоторое значение аргумента x = x 0 является корнем многочлена, то (x - x 0) является одним из сомножителей разложения этого многочлена по корням. Поэтому разделим числитель на (x – 1). Это деление можно выполнить «столбиком»:
. Здесь мы воспользуемся известным фактом, что если некоторое значение аргумента x = x 0 является корнем многочлена, то (x - x 0) является одним из сомножителей разложения этого многочлена по корням. Поэтому разделим числитель на (x – 1). Это деление можно выполнить «столбиком»:
x 5 – 2 x + 1 | x – 1
x 5 – x 4 x 4 + x 3 + x 2 + x - 1
x 4 – 2 x
x 4 – x 3
x 3– 2 x
x 3 – x 2
x 2– 2 x
x 2 – x
- x + 1
- x + 1
Следовательно, x 5 – 2 x + 1 = (x – 1)(x 4 + x 3 + x 2 + x – 1). Тогда, разлагая на множители разность кубов в знаменателе, получим:
 =
=  =
=
=  =
=  = 1.
= 1.
Пример 6. Найти  .
.
Решение. Это неопределенность вида [∞ - ∞]. Домножим функцию, стоящую под знаком предела, на сопряженную сумму  :
:

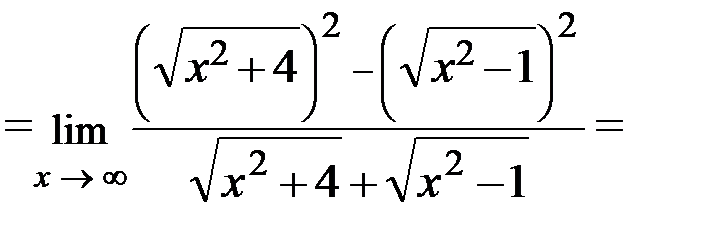

Пример 7. Найти 
Решение. Это задача с использованием первого замечательного предела  .
.
Обратим внимание на то, что при использовании первого замечательного предела нужно следить за аргументами частного под знаком предела. Они должны быть идентичны, т. е.  , т. к. аргумент и в числителе и в знаменателе равен 6 х и при х → 0 также 6 х → 0, а вот
, т. к. аргумент и в числителе и в знаменателе равен 6 х и при х → 0 также 6 х → 0, а вот  не является первым замечательным пределом, т. к. аргументы числителя и знаменателя не совпадают. В этом случае:
не является первым замечательным пределом, т. к. аргументы числителя и знаменателя не совпадают. В этом случае:
 =
= 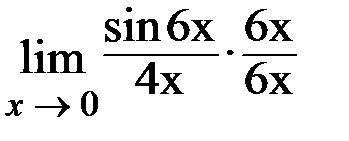 =
=  =
=
=  =
=  .
.
Пример 8. Найти  .
.
Решение. Это задача с использованием второго замечательного предела в первой форме  . Обратим внимание на то, что, как и при использовании первого замечательного предела, нужно следить за аргументами выражения в скобках и степени — они должны быть идентичны. Также заметим, что в обеих формах второго замечательного предела в скобках стоит сумма.
. Обратим внимание на то, что, как и при использовании первого замечательного предела, нужно следить за аргументами выражения в скобках и степени — они должны быть идентичны. Также заметим, что в обеих формах второго замечательного предела в скобках стоит сумма.
 =
=  =
=  = ℮15.
= ℮15.
Пример 9. Найти  .
.
Решение. Чтобы применить второй замечательный предел, сначала преобразуем выражение в скобках, выделив единицу:
 =
=  =
=  =
=
=  =
=
=  = ℮-14.
= ℮-14.
Пример 10. Найти  .
.
Решение. Это задача с использованием эквивалентных бесконечно малых величин. Заменяя  эквивалентной б.м. 5х2, а (1 - cos2 x) эквивалентной б.м.
эквивалентной б.м. 5х2, а (1 - cos2 x) эквивалентной б.м.  = 2 x 2, получим
= 2 x 2, получим
 =
=  =
=  .
.
Контрольные задания.
Найти следующие пределы.
3.1. а)  ; б)
; б) 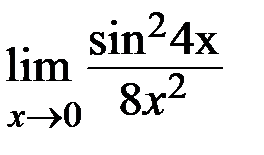 .
.
3.2. а)  ; б)
; б)  .
.
3.3. а)  ; б)
; б) 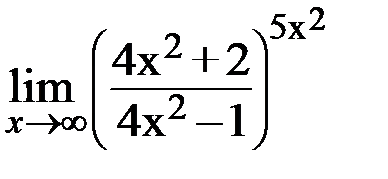 .
.
3.4. а)  ; б)
; б)  .
.
3.5. а)  ; б)
; б)  .
.
3.6. а)  ; б)
; б)  .
.
3.7. а)  ; б)
; б)  .
.
3.8. а)  ; б)
; б)  .
.
3.9. а)  ; б)
; б)  .
.
3.10. а)  ; б)
; б)  .
.
1.11. а)  ; б)
; б) 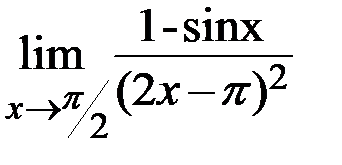 .
.
3.12. а)  ; б)
; б)  .
.
3.13. а)  ; б)
; б)  .
.
3.14. а)  ; б)
; б) 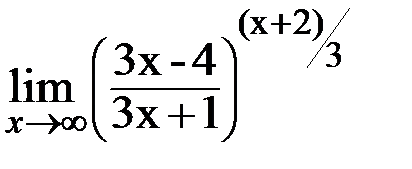 .
.
3.15. а)  ; б)
; б) 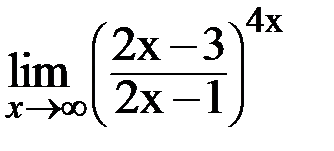 .
.
3.16. а)  ; б)
; б)  .
.
3.17. а) 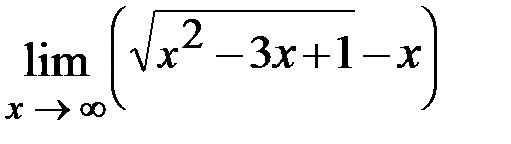 ; б)
; б)  .
.
3.18. а)  ; б)
; б) 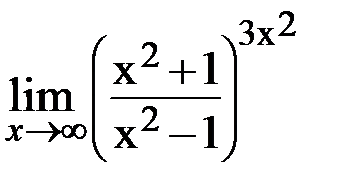 .
.
3.19. а)  ; б)
; б)  .
.
3.20. а)  ; б)
; б)  .
.






