Пропорции и пропорционирование

 

Сравнение двух величин мы называем отношением. Для образования пропорции необходимо два или несколько взаимосвязанных отношений. Композиционной значимостью обладают именно пропорции, в которых раскрываются внутренние закономерности связи формы.

Отдельно взятое отношение не может быть ни прекрасным, ни безобразным. Эстетическую значимость оно получает, лишь войдя в закономерную связь с другими, образуя пропорции. Пропорции – это соразмерность частей между собой и с целым. Пропорции служат средством гармонизации формы изделия. Простыми отношениями называют такие отношения в которых зависимость двух величин выражается дробным числом, где числитель и знаменатель целые числа в пределе от одного до шести (условно).

Пропорции – это одно из классических средств композиции, с помощью которого достигается организованность формы.

Масштаб и пропорции неразрывно связаны между собой.

Пропорции – это равенство двух отношений. Например: a/b=c/d.

Каждое промышленное изделие, каждое здание имеет свои пропорции. Пропорциональный, значит находящийся в определенном отношении к какой-либо величине.

Пропорциональные величины – величины, зависящие друг от друга таким образом, что с увеличением одной из них в несколько раз, соответственно во столько же раз увеличивается другая величина. В противном случае пропорции нарушаются. Размерные отношения элементов формы – это та основа, на которой строится вся композиция.

Как бы ни были хороши детали изделия, если всю объемно-пространственную не объединяет четкая пропорциональная система, трудно рассчитывать на целостность формы.

Пропорционирование – это творческий процесс, поэтому, каждое сооружение, каждое промышленное изделие представляет целую систему размерных отношений, определяющую функциональное назначение предмета.

Нельзя пропорционировать, например, станок, прежде чем определится его кинематическая схема. Пропорция учитывает конкретные условия, место и назначение предмета. В предметном мире, как и в мире природы все должно быть взаимосвязано пропорциями.

Пропорции имеют большое художественное значение. Они определяют соразмерность и гармоничность элементов формы, всех ее частей друг с другом и с целым.

Исследованию пропорций посвящали свои труды ученые, зодчие и художники античности и эпохи Ренессанса: Витрувий, Палладио, Виньола, Серлио и др. В наше время изучением пропорций занимались Э.Мессель, Д.Хэмбидж, М.Гика, крупные советские архитекторы и искусствоведы И.М. Жолтовский, А.Г. Габричевский, И.Б. Михайловский, Б.М. Михайлов, Л.Н. Павлов.

Леон-Батиста Альберти писал: «Красота – есть строгая соразмерная гармония».

Именно поэтому, пропорциональный строй, соразмерность частей и целого служат важной проверкой технического совершенства конструкций.

Если же, пренебрегая инженерной стороной, дизайнер рисует форму только ради «красивых» пропорций, неизбежно возникают конструктивно неоправданные пустоты за кожухами, увеличиваются габариты и масса станка.

Итак, пропорции связаны с основой конструкции, и от этого нельзя абстрагироваться.

Существует два основных подхода к пропорционированию различных промышленных изделий.

I – строится на относительной свободе проектировщика в выборе пропорций, когда он может задавать пропорции идя от формы к конструкции. Например при проектировании мебели.

II – иного подхода требуют изделия со сложной объемно-пространственной структурой, размерные отношения которых определяются конструкцией. Здесь необходимо вовремя корректировать пропорциональный строй формы как в целом, так и в отдельных ее элементах.

Среди других способов пропорционирования особенно выделяется так называемое «Золотое сечение».

 

 

2.5.1.1 Золотое сечение – гармоническая пропорция

 

 

Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.

В математике пропорцией (лат. proportio) называют равенство двух отношений: a: b = c: d.

Отрезок прямой АВ можно разделить на две части следующими способами:

• на две равные части – АВ: АС = АВ: ВС;
• на две неравные части в любом отношении (такие части пропорции не образуют);
• таким образом, когда АВ: АС = АС: ВС.

Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему

a: b = b: c или с: b = b: а.

Рис. 2.41 - Геометрическое изображение золотой пропорции

Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.

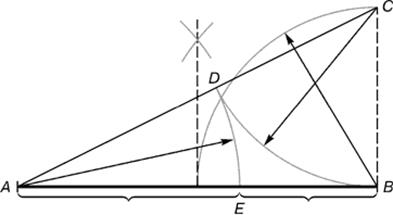
Рис. 2.42 - Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC

Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.

Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618..., если АВ принять за единицу, ВЕ = 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.

Свойства золотого сечения описываются уравнением:

x ² – x – 1 = 0.

Решение этого уравнения:

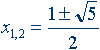
Свойства золотого сечения создали вокруг этого числа романтический ореол таинственности и чуть ли не мистического поклонения.

 

 

Второе золотое сечение

 

 

Болгарский журнал «Отечество» (№10, 1983 г.) опубликовал статью Цветана Цекова-Карандаша «О втором золотом сечении», которое вытекает из основного сечения и дает другое отношение 44: 56.

Такая пропорция обнаружена в архитектуре, а также имеет место при построении композиций изображений удлиненного горизонтального формата.

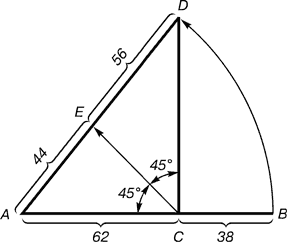
Рис. 2.43 - Построение второго золотого сечения

Деление осуществляется следующим образом (рис. 2.43, 2.44). Отрезок АВ делится в пропорции золотого сечения. Из точки С восставляется перпендикуляр СD. Радиусом АВ находится точка D, которая соединяется линией с точкой А. Прямой угол АСD делится пополам. Из точки С проводится линия до пересечения с линией AD. Точка Е делит отрезок AD в отношении 56: 44.

 

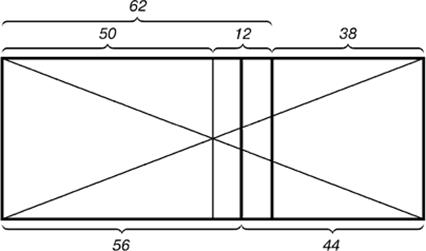
Рис. 2.44 - Деление прямоугольника линией второго золотого сечения

На рисунке 2.44 показано положение линии второго золотого сечения. Она находится посередине между линией золотого сечения и средней линией прямоугольника.

Золотой треугольник

 

 

Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой.

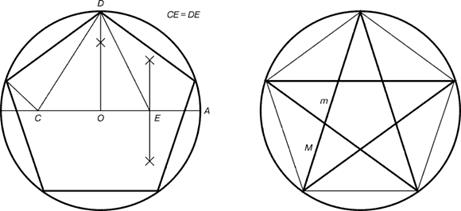
Рис. 2.45 - Построение правильного пятиугольника и пентаграммы

Для построения пентаграммы (рис. 2.45) необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471...1528). Пусть O – центр окружности, A – точка на окружности и Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.

Каждый конец пятиугольной звезды представляет собой золотой треугольник (рис. 2.46). Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

 

 

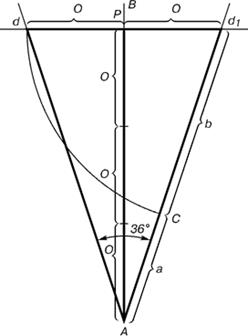
Рис. 2.46 - Построение золотого треугольника

 

Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d ₁ соединяем прямыми с точкой А. Отрезок dd ₁ откладываем на линию Ad ₁, получая точку С. Она разделила линию Ad ₁ в пропорции золотого сечения. Линиями Ad ₁ и dd ₁ пользуются для построения «золотого» прямоугольника.

 

 

История золотого сечения

 

 

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников (рис. 2.47).

 

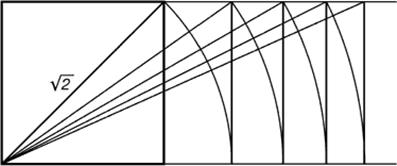
Рис. 2.47 - Динамические прямоугольники

Платон (427...347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.

В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

 

Рис. 2.48 – Античный циркуль золотого сечения

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.

Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок – бога отца, а весь отрезок – бога духа святого).

Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.

В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет. «Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать».

Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица – ртом и т.д. Известен пропорциональный циркуль Дюрера.

Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).

Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».

Построение ряда отрезков золотой пропорции (рис. 2.49) можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).

Если на прямой произвольной длины, отложить отрезок m, рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов

Рис. 2.49 – Построение шкалы отрезков золотой пропорции

В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». Вновь «открыто» золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».

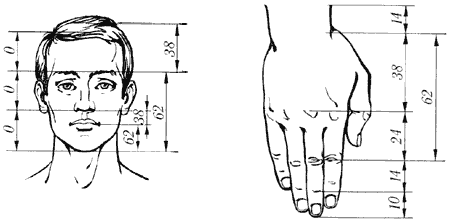
Рис. 2.50 - Золотые пропорции в частях тела человека

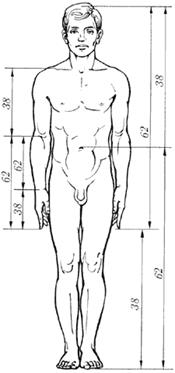
Рис. 2.51 - Золотые пропорции в фигуре человека

Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон (рис. 2.50, 2.51). Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13: 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8: 5 = 1,6. У новорожденного пропорция составляет отношение 1: 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону. Следующая его книга имела название «Золотое деление как основной морфологический закон в природе и искусстве». В 1876 г. в России была издана небольшая книжка, почти брошюра, с изложением этого труда Цейзинга. Автор укрылся под инициалами Ю.Ф.В. В этом издании не упомянуто ни одно произведение живописи.

В конце XIX – начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и т.д.

Ряд Фибоначчи

 

 

С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:

Месяцы 0 1 2 3 4 5 6 7 8 9 10 11 12 и т.д. Пары кроликов 0 1 1 2 3 5 8 13 21 34 55 89 144 и т.д.

Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21: 34 = 0,617, а 34: 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618: 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.

Фибоначчи так же занимался решением практических нужд торговли: с помощью какого наименьшего количества гирь можно взвесить товар? Фибоначчи доказывает, что оптимальной является такая система гирь: 1, 2, 4, 8, 16...