¬≥домо, що пр€ма л≥н≥€ в простор≥ визначаЇтьс€ положенн€м двох њњ точок. “аким чином, досить виконати комплексне кресленн€ цих двох точок, а пот≥м з`Їднати однойменн≥ проекц≥њ точок пр€мими л≥н≥€ми, отримаЇмо в≥дпов≥дно горизонтальну, фронтальну ≥ проф≥льну проекц≥њ пр€моњ.
¬≥дносно площин проекц≥й пр€ма може займати р≥зн≥ положенн€. ѕр€м≥, паралельн≥ одн≥й ≥з площин проекц≥й, називають пр€мими р≥вн€.
Ќазва њх залежить в≥д того, €к≥й площин≥ вони паралельн≥. ѕр€му, паралельну горизонтальн≥й площин≥ проекц≥й, називають горизонталлю ≥ позначають на кресленн€х через h (рис. 1.2.1) h2 ll x,  =
=  ,
,  Ц кут нахилу пр€моњ ј¬ до площини ѕ2.
Ц кут нахилу пр€моњ ј¬ до площини ѕ2.

|
|
–исунок 1.2.1
ѕр€му, паралельну фронтальн≥й площин≥ проекц≥й, називають фронталлю ≥ позначають через f (рис. 1.2.2.).
f1 ll х,  =
=  ,
,  Ц кут нахилу пр€моњ —D до площини ѕ1.
Ц кут нахилу пр€моњ —D до площини ѕ1.
ѕр€му, паралельну проф≥льн≥й площин≥ проекц≥й, називають проф≥льною пр€мою ≥ позначають через p (рис. 1.2.3).
p2  ’, p1
’, p1  ’,
’,  =
=  ,
,  та
та  Ц кути нахилу пр€моњ EF до площин ѕ1 та ѕ2.
Ц кути нахилу пр€моњ EF до площин ѕ1 та ѕ2.
ѕр€м≥, перпендикул€рн≥ одн≥й ≥з площин проекц≥й, називаютьс€ проекц≥ювальними, при цьому вони одночасно паралельн≥ двом ≥ншим площинам проекц≥й. ” проекц≥ювальних пр€мих одна проекц≥€ вироджуЇтьс€ в точку, а дв≥ ≥нш≥ проекц≥њ паралельн≥ сам≥й пр€м≥й ≥ зб≥гаютьс€ з напр€мом л≥н≥њ зв`€зку.

|
|
–исунок 1.2.2

|
|
–исунок 1.2.3
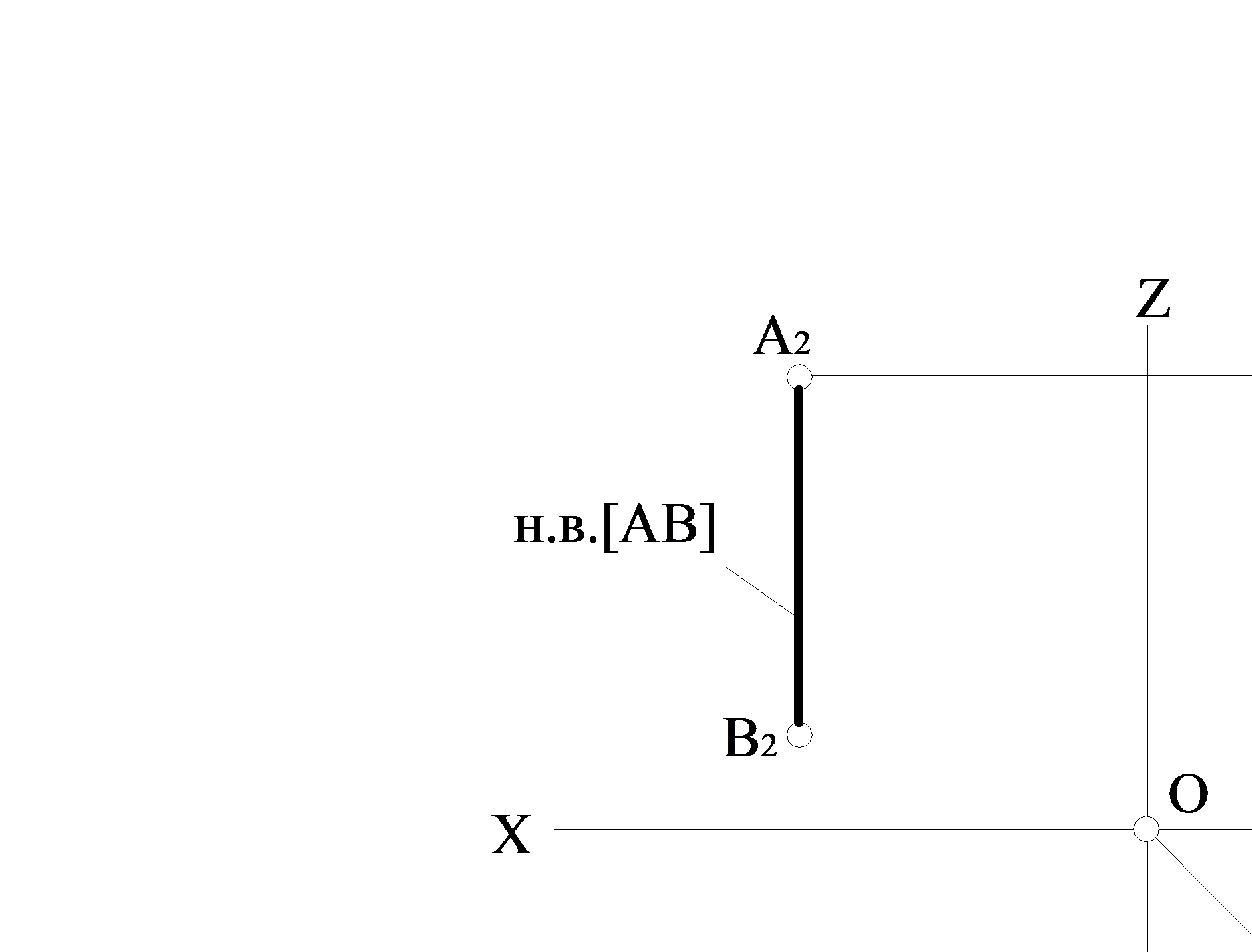
ѕр€му, перпендикул€рну горизонтальн≥й площин≥ проекц≥њ ѕ1 ≥ одночасно паралельну фронтальн≥й ѕ2 ≥ проф≥льн≥й ѕ3 площинам проекц≥й, називають горизонтально проекц≥ювальною (рис. 1.2.4).
|
|
–исунок 1.2.4
ѕр€му, перпендикул€рну фронтальн≥й площин≥ проекц≥й ѕ2 ≥ одночасно паралельну горизонтальн≥й ѕ1 та проф≥льний ѕ3 площинам проекц≥й, називають фронтально проекц≥ювальною (рис. 1.2.5).

|
|
–исунок 1.2.5
ѕр€му перпендикул€рну проф≥льн≥й площин≥ проекц≥й ѕ3 ≥ одночасно паралельну горизонтальн≥й ѕ1 та фронтальн≥й ѕ2 площинам проекц≥й, називають проф≥льно проекц≥ювальною (рис. 1.2.6)
ѕр€му, €ка не паралельна ≥ не перпендикул€рна жодн≥й ≥з площин проекц≥й, називають пр€мою загального положенн€. ѕриклад такоњ пр€моњ наведено на рис. 1.2.7. ¬≥др≥зок 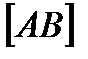 пр€моњ на жодну ≥з площин проекц≥й не в≥дображаЇтьс€ в натуральну величину, тобто
пр€моњ на жодну ≥з площин проекц≥й не в≥дображаЇтьс€ в натуральну величину, тобто  <
< 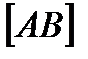 ,
,  <
<  ,
, 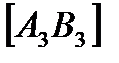 <
<  . ѕр€ма загального положенн€ маЇ р≥зн≥ кути нахилу до площин проекц≥й. ѕ≥д кутом нахилу пр€моњ до площини проекц≥й розум≥ють такий кут, €кий утворюЇтьс€ м≥ж самою пр€мою та њњ в≥дпов≥дною проекц≥Їю.
. ѕр€ма загального положенн€ маЇ р≥зн≥ кути нахилу до площин проекц≥й. ѕ≥д кутом нахилу пр€моњ до площини проекц≥й розум≥ють такий кут, €кий утворюЇтьс€ м≥ж самою пр€мою та њњ в≥дпов≥дною проекц≥Їю.
|
|
|
|
|
–исунок 1.2.6
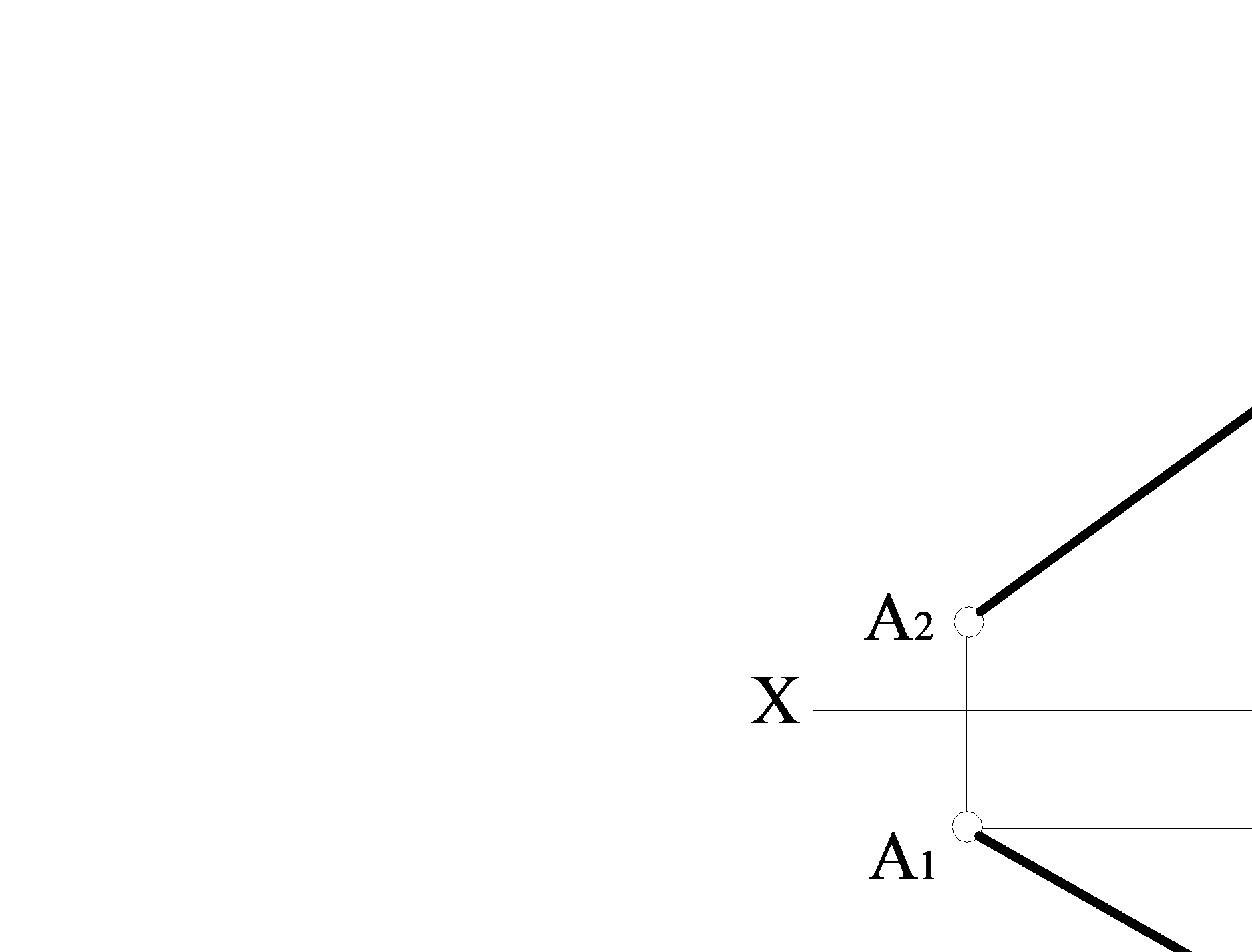
–исунок 1.2.7
ѕр€ма може належати одн≥й ≥з площин проекц≥й. Ќа рис. 1.2.8 наведено приклад пр€моњ ј¬, що належить горизонтальн≥й площин≥ проекц≥й ѕ1.
Ќа рис. 1.2.9 наведено приклад пр€моњ CD, що належить фронтальн≥й площин≥ проекц≥й ѕ2.
Ќа рис. 1.2.10 наведено приклад пр€моњ EF, що належить проф≥льн≥й площин≥ проекц≥й ѕ3.

|

|
–исунок 1.2.8
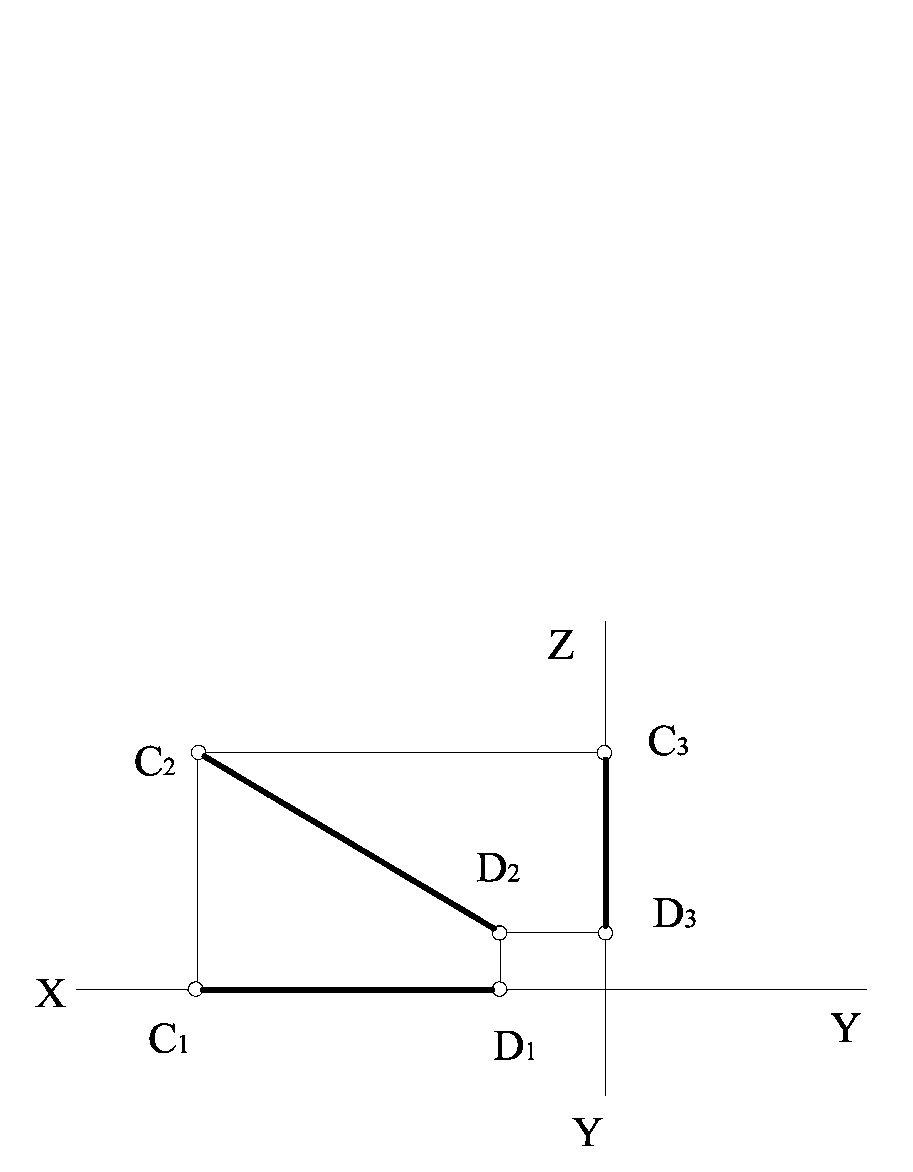
|
–исунок 1.2.9

|
|
–исунок 1.2.10






 = ќ’ ^ ј1¬1 = ј¬ ^ ѕ2
= ќ’ ^ ј1¬1 = ј¬ ^ ѕ2

 = OX ^ C2D2 = CD ^ ѕ1
= OX ^ C2D2 = CD ^ ѕ1
 ќ’
p1
ќ’
p1  ќ’
E3F3 =
ќ’
E3F3 = 
 = OY ^ P3 = EF ^ ѕ1
= OY ^ P3 = EF ^ ѕ1
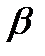 = OZ ^ P3 = EF ^ ѕ2
= OZ ^ P3 = EF ^ ѕ2
 ѕ1
AB װ ѕ2, AB װ ѕ3
A2B2 װ OZ
A3B3 װ OZ
A1
ѕ1
AB װ ѕ2, AB װ ѕ3
A2B2 װ OZ
A3B3 װ OZ
A1  (¬1) Ц точка
(¬1) Ц точка
 ѕ2
CD װ ѕ1
CD װ ѕ3
C1D1 װ OY
C3D3 װ OY
C2
ѕ2
CD װ ѕ1
CD װ ѕ3
C1D1 װ OY
C3D3 װ OY
C2 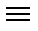 (D2) Ц точка
(D2) Ц точка
 (F3)
(F3)
 ѕ3
EF װ ѕ1
EF װ ѕ2
E1F1 װ OX
E2F2 װ OX
E3
ѕ3
EF װ ѕ1
EF װ ѕ2
E1F1 װ OX
E2F2 װ OX
E3 


