Рассмотрим расчет простого гидравлически короткого трубопровода. При этом используем уравнение Бернулли и другие уравнения, приведенные выше.
Расчет начинается с составления уравнения Бернулли для расчетной схемы, при этом придерживаются следующей методики.
1. Выбирают положение плоскости сравнения.
Обязательным требованием при выборе положения плоскости сравнения является ее горизонтальность, т.е., она должна быть перпендикулярна линии действия сил тяжести. Для упрощения расчетов и исключения возможных ошибок при определении геометрических напоров, плоскость сравнения 0-0 выбирают таким образом, чтобы 
. Но иногда целесообразно выбирать и другие положения плоскости сравнения, например, вдоль оси горизонтальной части трубопровода. Пример выбора плоскости сравнения приведен на рисунке 45.
Рисунок 45 - Схемы трубопроводов
2. Выбирают расчетные сечения.
Часто уравнение Бернулли применяется для определения разности пьезометрических напоров, под действием которых жидкость с заданным расходом Q движется в напорных трубопроводных системах. Если же напор известен, то по уравнению определяют расход жидкости или необходимый диаметр трубопровода. Для сокращения числа неизвестных величин, входящих в уравнение Бернулли, целесообразно сечения 1-1 и 2-2 выбирать таким образом, чтобы наибольшее количество членов уравнения было известно, или же легко определялось. Величины давлений выбирают как в абсолютных, так и в относительных значениях, но в идентичных значениях для обоих сечений. Если в сечении 1-1 выбрана величина избыточного давления, то и в сечении 2-2 тоже должно быть указано избыточное давление. В тех случаях, когда в одном из сечений давление равно атмосферному, давление удобнее выбирать в избыточных значениях.
3. Конкретизируют уравнение Бернулли для конкретной расчетной схемы трубопровода. Т.е. подставляют известные величины в уравнения и выясняют неизвестные.
Для лучшего понимания рассмотрим пример составления уравнения Бернулли для трубопровода, представленного на рисунке 46. Выбираем плоскость сравнения 0-0 таким образом, что все сечения напорной системы лежат выше этой плоскости, а центр тяжести выходного сечения трубопровода совпадает с ней. Выбираем расчетные сечения:
1-1 - по свободной поверхности жидкости в напорном резервуаре, 2-2 - на выходе из трубопровода.
В сечениях 1-1 и 2-2 известны следующие величины (см. рис.46):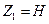 
, 
, 
, (так как приток и отток из резервуара равны между собой), , 
, 
.
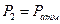Рисунок 46 - Расчетная схема трубопровода
Таким образом, после подстановки указанных величин в исходное уравнение, получим конечный вид уравнения Бернулли для случая, представленного на рисунке 46:
.
В уравнении пока неизвестны скоростной напор в конечном сечении и потери напора в трубопроводе (
; 
).
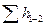Определение потерь напора будет рассмотрено ниже, а скоростной напор определяется с использованием уравнения неразрывности. Из уравнений неразрывности следует, что скорости обратно пропорциональны площадям живых сечений:
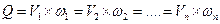
Тогда по известному расходу можно найти значение скорости в конечном сечении и скоростной напор .
4. Определяют потери напора 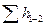. Отметим, что расчет потерь связан с выявлением характерных гидравлических сопротивлений. Потери напора слагаются из потерь двух видов:
- потерь напора на преодоление гидравлических сопротивлений по длине, пропорциональных длине участков русла или трубы, по которым движется жидкость, т.е. потерь на трение 
;
- потерь напора на преодоление гидравлических сопротивлений в пределах коротких участков в непосредственной близости к тем или иным местным конструктивным устройствам (вход, выход, расширение, сужение, поворот, трубопроводная арматура, фасонина и т.п.), т.е. местных потерь напора 
.
Принимается, что общие потери напора в системе равны сумме потерь напора по длине отдельных участков и всех местных потерь напора:
.
Для расчета потерь по длине (на трение) и местных потерь пользуются формулами Дарси-Вейсбаха и Вейсбаха:
, 
.
После того, как получен окончательный вид уравнения Бернулли и выявлены все возможные потери напора, определяют тип задачи, которую необходимо решить:
• Определение перепада напора Н (потребного напора), необходимого для пропуска заданного расхода жидкости по заданному трубопроводу (с известными длинами и диаметрами).
Эту задачу можно решить аналитически достаточно просто, используя конечный вид уравнения Бернулли для системы, подставив в него все известные величины, рассчитав потери напора.
• Определение расхода жидкости, который может пропустить заданный трубопровод с известным диаметром, длиной и перепадом давлений в начальном и конечном сечении (известной потерей напора).
Задачу этого типа решить аналитически достаточно трудно, т.к. скорость V и коэффициент Дарси 
зависит от расхода Q, который в начале расчета неизвестен.
При решении задачи используют или метод последовательных приближений (итерации) или графо-аналитический метод. При этом задаются рядом значений расхода Q и добиваются равенства левой и правой частей уравнения Бернулли. При использовании метода итерации получается большой объем вычислений. При использовании графо-аналитического метода достаточно трех-четырех приближений, после чего строится график зависимости Σh1-2=f(Q) и по нему определяется искомый расход. Пример построения зависимости Σh1-2=f(Q) показан на рисунке 47.
Рисунок 47 - Графо-аналитический метод
Определение необходимого диаметра трубопровода, обеспечивающего пропуск известного расхода при заданных длине и перепаде напоров (давлений).
Как и в предыдущем случае используются методы последовательного приближения или графо-аналитический, но задаются несколькими значениями диаметра и по результатам расчета строят график зависимости 
(d), по нему и подбирают искомый диаметр.
Пример решения этой задачи графо-аналитическим методом приведен на рисунке 48.
Рисунок 48 - Применение графо-аналитического метода.
5. Следующим пунктом расчета является построение напорной и пьезометрической линий.
После того, как решением уравнения Бернулли установлены напоры в начальном и конечном сечениях, расход и потери напора, можно приступить к построению напорной линии.
Построение напорной линии начинается с исходного сечения 1-1. Определяем для него гидродинамический напор с учетом того, что , а следовательно, 
. Если бы на пути от сечения 1-1 до сечения 6-6 не было бы сопротивлений, то потери напора не происходило бы и напорная линия оказалась бы параллельной плоскости сравнения 0-0, исходя из сечения 1-1. Гидравлические сопротивления, возникающие в реальной жидкости, будут приводить к уменьшению исходного напора на величину потерь на трение и местные сопротивления. При построении напорной линии эти потери откладываются вниз от исходного значения напора.
Потеря на вход на участке 1-2 понизит напорную линию на величину hм, на трение на участке 2-3 на величину hтр, и т.д. (см. рис.49). В итоге мы получим ломаную линию, показывающую изменение напора при движении жидкости из сечения 1-1 в сечение 6-6. Интенсивность потерь напора (энергии) называется гидравлическим уклоном, который равен отношению потерь напора на трение по длине hтр, к длине участка li.
Пьезометрическую линию строят следующим образом:
- определяют скоростной напор 
на каждом участке постоянного диаметра;
- откладывают вниз от напорной линии соответствующие значения величин скоростного напора
Получаем ломаную линию, называемую пьезометрической линией. Как видно пьезометрическая линия на участке проходит параллельно и ниже напорной на величину скоростного напора на участке. На участках, где происходит изменение диаметров трубопровода, параллельность нарушается из-за различия скоростных напоров αiVi/2g и αi+1 Vi+1/2g.
Рисунок 49 - Пример построения пьезометрической и напорной линий.
