Для решения задачи будем использовать дискретно-аналитический метод, который состоит в следующем: по оси x осуществляется конечно-разностная аппроксимация, а по оси времени t рассматривается непрерывная задача (рис. 4.3).
Рис. 4.3. Схема дискретизации.
Введем обозначения:
; 
, 
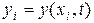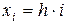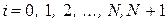, (4.55)
где в простейшем случае
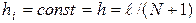. (4.56)
Здесь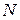 
– количество внутренних узлов конечно-разностной сетки, причем пусть 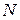– нечетное число.
Для всех внутренних узлов 
получим конечно-разностное уравнение – дискретный аналог уравнения колебаний (4.54):
, 
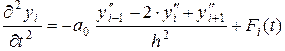, (4.57)
где
(4.58)
– вторая конечная разность, приближенно представляющая вторую производную от искомой функции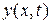 
по аргументу 
.
В соответствии с краевыми условиями из (4.54) для граничных узлов, очевидно, можем записать:
; 
; 
; 
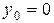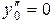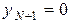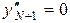. (4.59)
C учетом (4.59) преобразуются уравнения (4.57) Имеем:
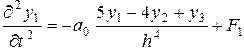; (4.60)
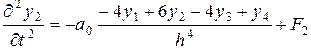; (4.61)
, 
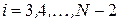; (4.62)
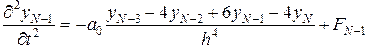; (4.63)
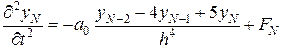. (4.64)
Обоснуем, например, (4.60) и (4.61):
;
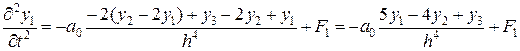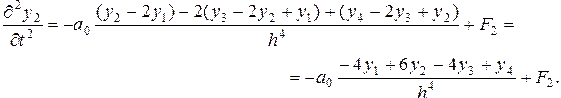
Введя обозначение
, (4.65)
можем представить разрешающую систему конечно-разностных уравнений (4.60)-(4.64) в матричном виде
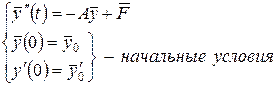(4.66)
где
. (4.67)
Заметим, что матрица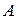 
положительно определена, т.е. все ее собственные числа положительные (в этом можно убедиться при их непосредственном вычислении).
Общее решение задачи (4.66) имеет вид:
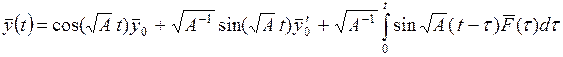. (4.68)
По условию рассматриваемой задачи
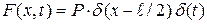, (4.69)
откуда следует, что
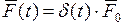, где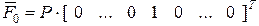 
. (4.70)
Это значит, что в векторе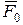 
лишь один «срединный элемент» (с номером 
) равен единице, а остальные элементы равны нулю. Ненулевой элемент вектора соответствует узлу конечно-разностной сетки с координатой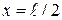 
, в котором в момент времени 
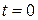приложено сосредоточенное ударное воздействие величиной 
.
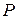Подставив (4.69) в (4.68), получим окончательный вид общего решения:
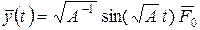. (4.71)
Варианты задания.
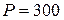– величина приложенного сосредоточенного ударного воздействия; 
; 
; 
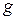– номер группы, 
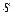– номер студента по журналу.
Принять количество количество внутренних узлов конечно-разностной сетки 
.
Пример соответствующего M-файла (ниже задано 
, 
):
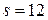function blow_f
g=input('g=');
s=input('s=');
n=input('n=');
L=300;P=300;
h=L/(n+1);
alfa=10^8*(100+g+s);
x=0:h:L;
a0=6*eye(n);a0(1,1)=5;a0(n,n)=5;
a1=ones(n-1,1);
a2=ones(n-2,1);
A=a0-4*(diag(a1,-1)+diag(a1,1))+diag(a2,-2)+diag(a2,2)
A=alfa*A/h^4;
F=zeros(n,1);F((n+1)/2)=P;
sq_A=sqrtm(A);
fJ=sqrt(eig(A));
t0=pi/(4*fJ(n));
tmax=125*t0;
nt=3;
t=[t0,tmax/2,tmax];
res=zeros(nt,n+2);
fprintf('\n прогиб балки Y(x,t)\n')
for i=1:nt
Y_t=inv(sq_A)*funm(sq_A*t(i),'sin')*F;
res(i,2:n+1)=Y_t';
fprintf('Y(%6.4f):',t(i)),fprintf('%8.4f',res(i,:)),fprintf('\n')
end
hold on
plot(x,res(1,:),'.-')
plot(x,res((nt+1)/2,:),'o-.r')
plot(x,res(nt,:),'*:g')
grid on
s1=sprintf('t=%6.4f',t(1));
s2=sprintf('t=%6.4f',t((nt+1)/2));
s3=sprintf('t=%6.4f',t(nt));
legend(s1,s2,s3,0)
title(sprintf('Y(x,t)=-inv(sqrt(A))*sin(sqrt(A)t))*F\n%s %s %s', s1,s2,s3))
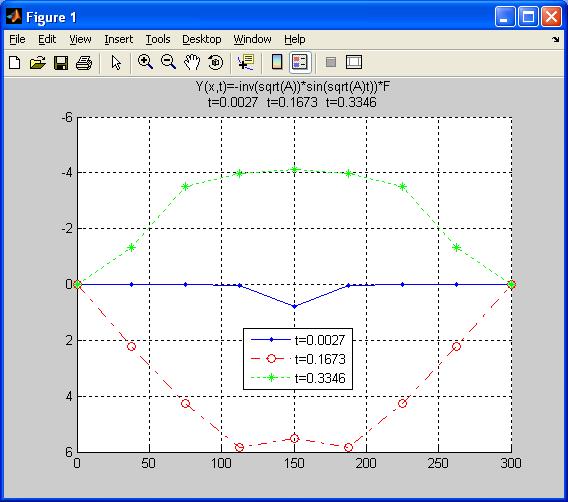
Результаты расчета:
g=3
s=12
n=7
A =
5 -4 1 0 0 0 0
-4 6 -4 1 0 0 0
1 -4 6 -4 1 0 0
0 1 -4 6 -4 1 0
0 0 1 -4 6 -4 1
0 0 0 1 -4 6 -4
0 0 0 0 1 -4 5
прогиб балки Y(x,t)
Y(0.0027): 0.0000 -0.0001 -0.0053 0.0217 0.7703 0.0217 -0.0053 -0.0001 0.0000
Y(0.1673): 0.0000 2.2085 4.2797 5.8565 5.5146 5.8565 4.2797 2.2085 0.0000
Y(0.3346): 0.0000 -1.3399 -3.5149 -3.9787 -4.1294 -3.9787 -3.5149 -1.3399 0.0000
>>
Замечание. Здесь вычисление функций от матрицы A реализуются следующим образом:
Ø 
с использованием стандартной функции sqrtm(A),
Ø 
с использованием funm(sqrtm(A),’sin’).
| Function | Syntax for Evaluating Function at Matrix A |
| exp | funm (A, @exp) |
| log | funm(A, @log) |
| sin | funm(A, @sin) |
| cos | funm(A, @cos) |
| sinh | funm(A, @sinh) |
| cosh | funm(A, @cosh) |
Кроме того, для вычисления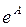 
, 
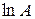и можно использовать встроенные функции expm(A), logm(A) и sqrtm(A), соответственно.
