Определение теоретического закона распределения случайных величин.

При увеличении объема выборки и количества интервалов разбиения ломаная линия эмпирической кривой распределения становится более плавной, т.е. при n®¥ кривая приближается к теоретической кривой распределения. Уравнение, описывающее кривую теоретического распределения, называется законом распределения.

Для эффективного анализа точности технологического процесса необходимо установить теоретический закон распределения данных выборочной совокупности. Затем, производя замену выборочного распределения теоретическим законом, свойства которого можно перенести на распределение выборки, облегчить работу технолога по анализу причин, формирующих качество контролируемых показателей.

Экспериментально установлено, что около 60% всех выходных технологических параметров обработки подчиняются закону нормального распределения, т.е. закону Гаусса. Этому же закону подчиняется и рассеяние размеров деталей, анализу которого посвящена данная самостоятельная работа.

Уравнение кривой нормального распределения имеет вид:

 

,

 

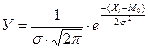Где У –плотность вероятности;

М₀ и s - параметры закона распределения;

Х_i – аргумент функции плотности вероятности, который представляет собой время безотказной работы;

е –основание натурального логарифма.

Кривая плотности вероятности нормального распределения (рис.1) симметрична относительно максимальной ординаты. Параметр представляет собой абсциссу, соответствующую оси симметрии кривой нормального распределения и называется математическим ожиданием. Этот параметр является теоретическим аналогом среднего арифметического значения D_ср. Параметр s называется теоретическим средним квадратичного отклонением и является теоретическим аналогом эмпирического (выборочного) среднего квадратичного отклонения S.

Положение и форма кривой зависят от величины и s. При изменении форма кривой остается прежней, смещаясь при этом по оси абсцисс. Величина s оказывает влияние на форму кривой распределения. Так, например, при уменьшении величины среднего квадратичного отклонения кривая «сжимается» по оси абсцисс и «вытягивается» вдоль оси ординат.

На теоретической кривой нормального распределения выделяют 5 характерных точек. Максимальную ординату кривой, соответствующую (точка 3, рис.1) определяют по формуле:

(10)

 

На расстоянии ±s от вершины кривая имеет две точки перегиба (точки 2 и 4, рис. 1) ординаты которой равны:

 

(11)

 

Кривая асимптотически приближается к оси абсцисс. На расстоянии ±3s от положения вершины кривой ее ветви так близко подходят к оси абсцисс, что в этих пределах оказывается 99,73% всей площади, т.е. практически 100%. Возникающая при этом погрешность 0,27% существенного значения для инженерных расчетов не имеет. Поэтому можно принять, что У_1,5=0.

Величина w=6s является фактическим полем рассеяния размеров деталей. Следует различать эмпирическое и фактическое поле рассеяния. Эмпирическое – определяется размахом R. Величина фактического поля рассеяния определяется для генеральной совокупности в предположении, что n®¥. Исходя из этого всегда w>R, причем разница w-R уменьшается с увеличением объема выборки.

Теоретический закон распределения оценивает генеральную совокупность. Если из этой совокупности берется представительная выборка, то на основании теории больших чисел можно считать, что распределение размеров деталей в выборке будет отражать характер распределения всей генеральной совокупности, тогда при статистических расчетах с некоторыми допущениями можно принять:

»D_ср ; а s»S.

Погрешность соответствия s и S зависит от числа элементов выборки n и учитывается поправочным коэффициентом Р, приведенным в табл.3.

 

Таблица 3.

Значения поправочного коэффициента Р в зависимости от объема выборки n

Значения коэф-та Р	Объем выборки n
1,46	1,4	1,37	1,31	1,28	1,25	1,22	1,20	1,16	1,14	1,12	1,10

 

 

Тогда: s=р*S=1,28*0,094=0,12 (12)

На практике фактическое поле рассеяния определяется с учетом погрешности по формуле:

=0,12*6=0,72 (13)

Определение w является важнейшей задачей анализа технологических процессов, поскольку только фактическое поле рассеяния размера деталей объективно отражает точность контролируемого параметра в реальных производственных условиях. Для построения теоретической кривой распределения для рассматриваемого примера необходимо значения ординат характерных точек выразить в единицах частоты, т.е.:

(14)

(15)

Абсциссы соответствующих точек равны:

(16)

(17)

(18)

(19)

(20)

Полученные точки соединяют плавной кривой (рис. 1, кривая 3.).