Построение эмпирической кривой распределения.

АНАЛИЗ НАДЕЖНОСТИ И ТОЧНОСТИ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА МЕХАНИЧЕСКОЙ ОБРАБОТКИ СТАТИСТИЧЕСКИМ МЕТОДОМ.

Цель работы: овладение практическими навыками анализа точности технологических процессов механической обработки деталей в условиях крупносерийного производства с использованием методов математической статистики.

Задачи работы:

-определение статистических характеристик точности технологического процесса;

- определение количества вероятного брака;

Статистический анализ точности технологического процесса механической обработки.

При обработке деталей на станках их размеры колеблются в определенных пределах, отличаясь друг от друга и от контролируемого размера на величину случайной погрешности. В результате этого образуется рассеяние размеров деталей, обработанных при одинаковых условиях. Для изучения и анализа закономерностей распределения размеров деталей при их рассеянии применяют методы математической статистики, в основе которых лежит использование выборочной совокупности или выборки.

Выборочной совокупностью называется часть деталей, которые отбираются из генеральной совокупности (общей партии) для получения достоверных сведений о всей генеральной совокупности. Генеральной называется совокупность всех возможных деталей, изготовляемых на данной операции и объединенных каким-либо признаком, который отражает интересующий технолога контролируемый параметр.

Причем, выборка должна быть представительной (репрезентативной), чтобы результаты выборки можно было использовать для анализа точности технологических процессов в условиях массового производства.

Число деталей n в выборке составляет ее объем. Большой выборочной совокупностью считается выборка при n>30, а малой n<30. От объема выборки зависит точность результата. Обычно в производственных условиях объем больших выборок, которые используются для анализа технологических процессов, составляет 50-200 штук деталей.

Построение эмпирической кривой распределения.

В табл.1 приведены результаты измерений наружного диаметра партии (выборки) деталей после токарной обработки, значения которого носят случайный характер D_i. При этом, детали считаются пригодными, если их размеры укладываются в интервал 100÷100,5 мм.

Таблица 1.

№п/п	D,мм	№п/п	D,мм	№п/п	D,мм	№п/п	D,мм	№п/п	D,мм
	100,20		100,22		100,32		100,19		100,28
	100,35		100,05		100,31		100,12		100,35
	100,36		100,18		100,31		100,10		100,23
	100,41		100,28		100, 09		100,26		100,25
	100,42		100,10		100,21		100,16		100,22
	100,17		100,12		100,22		100,16		100,35
	100,24		100,23		100,15		100,00		100,29
	100,22		100,18		100,05		100,37		100,23
	100,20		100,27		100,27		100,33		100,29
	100,22		100,15		100,26		100,40		100,20

 

Расположив полученные действительные размеры D_i в порядке возрастания их значений, получим ранжированный ряд случайных дискретных величин. Разность между наибольшим и наименьшим значением этого ряда определяет величину эмпирического поля рассеивания действительных размеров или размах значений выборки R, т.е.:

=100,42-100=0,42 (1)

Для сокращения времени расчетов поле рассеивания результатов измерений можно разбить на k интервалов, количество которых определяется по формуле Хайнкольда:

 

(2)

Ширина интервала можно определить по формуле:

(3)

При этом границы одинаковых интервалов выбирают так, чтобы значение D_min попало в первый интервал, а D_max – в последний.

Число деталей, попавшее в каждый интервал, называется частотой m_j. При определении значений частот придерживаются следующего правила: все значения размеров, попавшие на границы интервалов, должны учитываться в последующем интервале. Иногда при анализе значений выборки используют относительную величину частоты, т.е. частость, равную

В табл. 2. (столбцы 1-5) представлено эмпирическое распределение размеров деталей по данным табл.1.

Характер распределения значений случайной величины, которой является действительный размер обрабатываемой детали, более наглядно демонстрируется графически гистограммой или эмпирической кривой распределения. Для построения гистограммы, используя данные табл.2., по оси абсцисс в масштабе откладывается значения размеров интервалов, а по оси ординат – соответствующие им частоты или частости . В результате построения получается ступенчатая линия. Если последовательно соединить между собой точки, соответствующие ординатам середин каждого интервала, то образующаяся ломанная линия представляет собой эмпирической кривой распределения (рис.1.).

Таблица 2.

Распределение размеров деталей

№ интервала	Интервал действительных размеров, Di, мм	Частота, mj, шт.	Значения середин интервалов, Хj, мм	Частость,	Отклонения от моды, Uj =xj -Dр
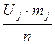
	100,00-100,06		100,03	0,06	-0,18	0,0324	0,0972	-0,54	-0,0108
	100,06-100,12		100,09	0,06	-0,12	0,0144	0,0432	-0,36	-0,0072
	100,12-100,18		100,15	0,14	-0,06	0,0036	0,0252	-0,42	-0,0084
	100,18-100,24		100,21	0,3
	100,24-100,30		100,27	0,2	0,06	0,0036	0,036	0,06	0,012
	100,30-100,36		100,33	0,14	0,12	0,0144	0,1008	0,84	0,0168
	100,36-100,42		100,39	0,1	0,18	0,0324	0,162	0,9	0,018
ИТОГО						0,4644		0,0204

 

Модальным интервалом является интервал №4, а его середина М_o =100,21 –модальным значением.