ФГБОУ ВПО
«РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГЕОЛОГОРАЗВЕДОЧНЫЙ УНИВЕРСИТЕТ ИМЕНИ СЕРГО ОРДЖОНИКИДЗЕ» МГРИ-РГГРУ
Кафедра РМСВМС и МД
Секция МД
ОСНОВЫ ГЕОДЕЗИИ ЛЕКЦИИ
Москва
2014
Предмет и задачи геодезии, ее связь с другими науками
Геодезия – это наука, рассматривающая методы и способы измерения земной поверхности, применение которых дает возможность определять форму и размеры земли, а также производить съемку (измерения) отдельных ее частей для изображения на картах, планах используемых для создания различных инженерных сооружений.
Геодезия включает в себя высшую и космическую геодезии, топографию, фотограмметрию и инженерную геодезию.
– Высшая геодезия – изучает фигуру и размер земли, методы определения координат точек на поверхности для территории всей страны.
– Космическаягеодезия – решает геодезические задачи с помощью искусственных спутников земли.
– Топография – рассматривает способы изучения земной поверхности, и изображение ее на картах и планах.
– Фотограмметрия – решает задачи измерений по аэро- фото- и космическим снимкам для различных целей.
– Инженерная геодезия – изучает методы геодезического обеспечения при разработке проектов, строительств, эксплуатации различных сооружений, а также при изучении освоении и охране природных ресурсов.
Геодезические работы разделяются на полевые и камеральные.
– Полевые работы состоят из измерений горизонтальных и вертикальных углов, а также горизонтальных, наклонных и вертикальных расстояний.
– Камеральные работы состоят из вычислений результатов полевых измерений и графических построений.
Формы и размеры земли
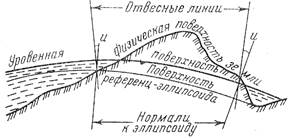Физическая поверхность земли представляет собой сочетание возвышенностей и углублений, которые, как правило, заполнены водой, поскольку большую часть поверхности земли составляет поверхность океанов и морей, то за общую фигуру земли приняли очертание поверхности воды в спокойном ее состоянии мысленно продолженным под материками. В любой точке эта поверхность перпендикулярна и т.о. везде горизонтальна, такая поверхность называется уровенной, приуроченная к среднему уровню океана и называется среднеуровенной поверхностью.
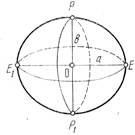Тело, ограниченное среднеуровенной поверхностью, называется геоидом. Вследствие неравномерности распределения масс в земной коре, поверхность геоида не является правильной геометрической поверхностью, поэтому, для изучения фигуры земли, используют правильное тело эллипсоид вращения, фигура, которая близка к геоиду. Она характеризуется большой и малой полуосями, и полярным сжатием.
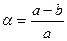– формула полярного сжатия.
Размеры земного эллипсоида, принятые как обязательные в нашей стране:
а=6 378 245 м
в=6 356 863 м
α=1:298
В исключительных случаях без ущерба для точности можно принимать землю за шар с R=6 371.11 км.
Системы координат
– делятся на плановые и высотные.
· 
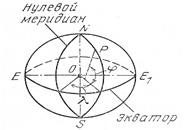Плановые системы координат. Географические координаты.
За основную поверхность проекции принимают поверхность эллипсоида и геоида.
За основные координатные линии принимают меридианы и параллели.
Меридиан – это сечение эллипсоида плоскостью проходящей через полярную ось NS.
Параллель – сечение эллипсоида плоскостью перпендикулярно7й полярной оси NS.
Долгота – это двугранный угол между плоскостью нулевого меридиана и плоскостью меридиана проходящего через определяемую точку. Отсчитывается к западу и востоку от нулевого меридиана, изменяется от 0º до 180º.
Широта – угол между плоскостью экватора и нормалью к эллипсоиду (отвесной линией) отсчитывается к северу и югу от экватора и изменяется от 0º до 90º.
· Плоские прямоугольные координаты
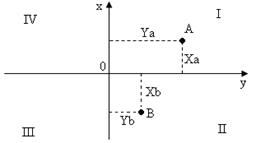– представляют собой две взаимно перпендикулярные прямые лежащие в горизонтальной плоскости. Точка пересечения прямых начало счета координат. Одна из прямых совпадает с меридианом и принимается за ось х, с положительным направлением на север, а вторая за ось у с положительным направление на восток.
Эта система координат применяется на небольших участках земной поверхности размерами не более 20х20 км.
В некоторых случаях ось х не совпадает с меридианом, в этом случае системакоординат называется частной или условной. Частные системы применяются при производстве инженерно–технических работ.
· Система координат Гаусса–Крюгера (зональная система координат)
В геодезии на плоскости изображаются значительные участки земной поверхности. Для этого применяются различные проекции, дающие возможность переносить изображение на плоскость при помощи математических законов. Для геодезии выгодно чтобы изображение не имело искажения в углах между направлениями (равноугольные проекции или конформные). К этой проекции изображение контуров будет подобным, масштаб практически постоянным и не зависеть от направления, искажения будут возникать только в длинах линий.
Суть проекции и соответствующей системы координат заключается в следующем.
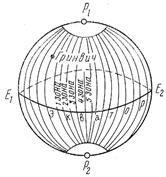
1. Земной эллипсоид при помощи меридианов делится на 6º или 3º зоны. Зоны нумеруют к востоку от нулевого меридиана, средний меридиан каждой зоны называется осевым.
2. Каждая зона в отдельности проектируется на плоскость таким образом, чтобы осевой меридиан и экватор изобразились прямыми линиями без искажений. Осевой меридиан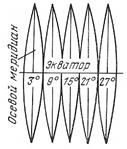 
принимается за ось х, с положительным направление на север, а экватор с положительным направлением на восток. Линии параллельны осевому меридиану и экватору, и образуют координатную сетку.
Искажения в этой системе координат возрастают по мере удаления от осевого меридиана (искажается длина). На границе зоны искажения длин линий будет ≈1/1500 для 6º зоны и ≈1/6000 для 3º зоны. Поправка за искажения длины линий будет вычислять по формуле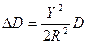 
.
D – длина отрезка
R – радиус земли
Y – средняя ордината отрезка.
3. Поскольку внутри каждой зоны системы координат одинаково возникают определенные положения точки на земной поверхности. Для установления зоны, в которой расположена точка, к значению ординаты слева приписывают номер зоны:
уа=1 532 371.15
ув=2 532 371.15
Чтобы не иметь отрицательных ординат точкам осевого меридиана условно приписывается ордината 500км.
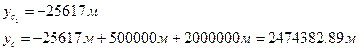
Высоты точек в геодезии называются отметками.
Отметка – это отвесное расстояние от начала счета высот до точки.
Если за начало счета высот принимать среднюю уровенную поверхность, система высот называется абсолютной, а отметки абсолютными.
В нашей стране за начало счета прият нуль Кранштадтского футштока, и система высот называется Балтийской.
Если за начало счета высот принимается произвольная уровенная поверхность, то система высот называется относительной, отметки относительными.
В горном деле за начало счета высот принимают отметку устья вскрываемой выработки.
Ориентирование линий
– это определение положения линий относительно каких–то исходных направлений.
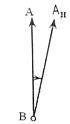
В качестве исходных направлений используется истинный магнитный и осевой меридианы, а в качестве ориентирных углов используют истинный и магнитный азимуты, дирекционный угол и румб.
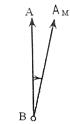Истинный азимут – это угол между северным направлением истинного меридиана и определяемой линией, отсчитывается по часовой стрелке и измеряется от 0º до 360º.
Магнитный азимут – это угол между северным направлением магнитного меридиана и определяемой линией, отсчитывается по часовой стрелке от 0º до 360º.
Поскольку истинный и магнитные полюса земли не совпадают, истинный и магнитный меридианы каждой точки, также не совпадает, а истинный и магнитный азимуты: различаются на величину магнитного склонения (δ).
Магнитное склонение – угол между северными концами истинного и магнитного меридианов. Магнитное склонение бывает восточным и западным, постоянно меняться. Различают вековое, годичное, суточное. Также существует магнитные аномалии, поэтому ориентирование по магнитному азимуту считается не надежным.
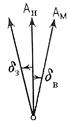
Связь между истинным и магнитным азимутом
Аи=Ам+ δв
Аи=Ам– δз
Дирекционный угол – это угол между северным направлением осевого меридиана или параллельной ему линии и определяемым направлением, отсчитывается по часовой стрелке от 0º до 360º.
Прямой и обратный азимуты и дирекционные углы.
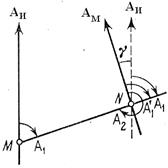Если направление линии MN с точки M на точку N считать прямым, то NM будет обратным направлением той же линии. В соответствии с этим угол А1 является прямым азимутом MN в точке М, а А2 – обратным азимутом той же линии в точке N.
Как следует из рисунка зависимость между прямым и обратным азимутами линии MN определится выражением
А2=А1+180º+γ
или в общем случае
Аобр=Апр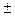 
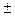180º γ
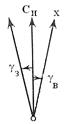
Угол сближения меридианов γ – угол между истинными меридианами двух точек или угол между северными концами истинного и осевого меридиана. Сближение между углами бывает восточным и западным.
