МИНИСТЕРСТВО ОБРАЗОВАНИЯ ТВЕРСКОЙ ОБЛАСТИ
ГБПОУ «Тверской колледж им. А.Н. Коняева»
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Элементы высшей математики»
специальность 09.02.03 «Программирование в компьютерных системах»
для студентов заочников
Разработчик: преподаватель Бодров Е.Н.
Тверь 2015
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ПОДГОТОВКЕ К ЭКЗАМЕНУ И ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
При изучении курса «Элементы высшей математики» рекомендуется использовать литературу:
Основные источники:
1. Баврин И.И. Курс высшей математики/И.И. Баврин – М.: ВЛАДОС, 2008. – 560 с.
2. Дадаян А. А. Математика/ А. А. Дадаян. – М.: ФОРУМ ИНФРА- М, 2007. – 544 с.
3. Дадаян А. А. Сборник задач по математике/ А. А. Дадаян. – М.: ФОРУМ ИНФРА- М, 2007. – 352 с.
4. Кремер Н.Ш. Высшая математика для экономистов/ Н.Ш. Кремер. – М.: ЮНИТИ-ДАНА, 2010. – 479 с.
5. Минорский В. П. Сборник задач по высшей математике/ В. П. Минорский. – М.: Физико-математическая литература, 2008. – 336 с.
Дополнительные источники:
1. Ильин В.А., Ким Г.Д. Линейная алгебра и аналитическая геометрия/В.А. Ильин, Г.Д. Ким. – М.: ТК Велби, Изд-во Проспект, 2007. – 400 с.
Интернет-ресурсы:
URL: http://www.math.ru/ (дата обращения: 25.08.2015).
При подготовке к экзамену рекомендуется:
1. Изучить теоретические вопросы, которые выносятся на экзамен;
2. Повторить решение задач, выполненных в контрольной работе;
3. Составить список непонятных вопросов и решений задач и задать их преподавателю на консультации перед экзаменом.
При выполнении контрольной работы следует руководствоваться следующими требованиями:
1. Работа должна быть представлена в срок, установленный графиком учебного процесса.
2. В начале работы должен быть указан номер варианта.
3. Перед решением задач необходимо указать их номер и полностью привести условие.
4. Работа должна быть правильно оформлена и выполнена четким, разборчивым почерком без применения сокращений слов.
5. Решение заданий должно быть подробным.
6. Каждое задание должно заканчиваться ответом.
Вариант соответствует порядковому номеру студента в журнале, если он более десяти, то в качестве варианта берётся количество единиц.
ЗАДАНИЯ КОНТРОЛЬНОЙ РАБОТЫ
ЗАДАНИЕ 1
Дана матрица  . Найдите
. Найдите  ,
,  .
.
1.  ,
,  .
.
2.  ,
,  .
.
3.  ,
,  .
.
4.  ,
,  .
.
5.  ,
,  .
.
6.  ,
,  .
.
7. 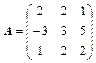 ,
,  .
.
8. 
 .
.
9.  ,
,  .
.
10. 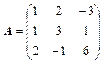 ,
,  .
.
ЗАДАНИЕ 2
Решите системы уравнений: а) по правилу Крамера; б) методом Гаусса; в) матричным методом.
1)  2)
2) 
3)  4)
4) 
5)  6)
6) 
7) 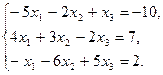 8)
8) 
9)  10)
10) 
ЗАДАНИЕ 3
Даны координаты вершин пирамиды АВСD. Требуется:
1) записать векторы  ,
,  ,
,  в системе орт
в системе орт  ,
,  ,
,  и найти модули этих векров;
и найти модули этих векров;
2) найти угол между векторами  ,
,  ;
;
3) найти площадь грани АВС;
4) найти объем пирамиды АВСD;
5) составить уравнение ребра АС;
6) составить уравнение грани АВС.
| А (1; 2; 1), В (-1; 5; 1), С (-1; 2; 7), D (1; 5; 9). | |
| А (2; 3; 2), В (0; 6; 2), С (0; 3; 8), D (2; 6; 10). | |
| А (0; 3; 2), В (-2; 6; 2), С (-2; 3; 8), D (0; 6; 10). | |
| А (2; 1; 2), В (0; 4; 2), С (0; 1; 8), D (2; 4; 10). | |
| А (2; 3; 0), В (0; 6; 0), С (0; 3; 6), D (2; 6; 8). | |
| А (2; 2; 1), В (0; 5; 1), С (0; 2; 7), D (2; 5; 9). | |
| А (1; 3; 1), В (-1; 6; 1), С (-1; 3; 7), D (1; 6; 9). | |
| А (1; 2; 2), В (-1; 5; 2), С (-1; 2; 8), D (1; 5; 10). | |
| А (2; 3; 1), В (0; 6; 1), С (0; 3; 7), D (2; 6; 9). | |
| А (2; 2; 2), В (0; 5; 2), С (0; 2; 8), D (2; 5; 10). |
ЗАДАНИЕ 4
Установите вид заданной кривой. Найдите основные параметры (для окружности – центр и радиус; для эллипса – оси, координаты фокусов, эксцентриситет; для параболы – координаты вершины, фокуса и уравнение директрисы; для гиперболы – оси, координаты фокусов, эксцентриситет, уравнения асимптот). Построите график.
1. а)  б)
б) 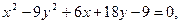 в)
в) 
| 6.а)  б)
б)  в)
в) 
|
2. а)  б)
б)  в)
в) 
| 7. а)  б)
б)  в)
в) 
|
3. а)  б)
б)  в)
в) 
| 8. а) 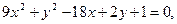 б)
б) 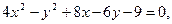 в)
в) 
|
4. а)  б)
б)  в)
в) 
| 9. а)  б)
б)  в)
в) 
|
5. а)  б)
б)  в)
в) 
| 10. а)  б)
б)  в)
в) 
|
ЗАДАНИЕ 5
Найдите сумму, произведение и частное чисел  и
и  :
:
1)  ,
,  ;
;
2)  ,
,  ;
;
3)  ,
,  ;
;
4) 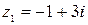 ,
,  ;
;
5)  ,
,  ;
;
6) 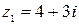 ,
,  ;
;
7)  ,
,  ;
;
8)  ,
, 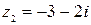 ;
;
9)  ,
,  ;
;
10)  ,
,  .
.
Программа экзамена
по дисциплине «Элементы высшей математики»
Преподаватель: Бодров Е.Н.
1. Матрицы, действия над матрицами. Примеры.
2. Определители. Свойства определителей.
3. Разложение определителя по элементам строки или столбца. Примеры.
4. Обратная матрица. Способы нахождения обратной матрицы. Примеры.
5. Системы линейных уравнений. Правило Крамера. Примеры.
6. Метод Гаусса. Примеры.
7. Матричный способ решения систем линейных уравнений.
8. Определение вектора. Координаты вектора. Линейные операции над векторами.
9. Нелинейные операции над векторами (скалярное, векторное и смешанное произведение). Примеры.
10. Уравнения прямой.
11. Уравнения плоскости.
12. Кривые второго порядка.
13. Числовые последовательности. Примеры.
14. Предел функции. Теоремы о пределах. Примеры.
15. Замечательные пределы. Примеры.
16. Односторонние пределы. Примеры.
17. Непрерывность функции. Точки разрыва. Примеры.
18. Производная функции. Производные основных элементарных функций. Примеры.
19. Вычисление производной по определению. Примеры.
20. Правила дифференцирования. Примеры.
21. Сложная функция и её производная. Примеры.
22. Дифференциал функции. Производные и дифференциалы функции.
23. Правило Лопиталя. Примеры.
24. Механический и геометрический смыслы производной.
25. Монотонность функции. Экстремумы функции. Примеры.
26. Выпуклость графика функции. Точки перегиба. Примеры.
27. Асимптоты. Примеры.
28. Исследование функций и построение их графиков.
29. Наибольшее и наименьшее значения функции на отрезке. Примеры.
30. Первообразная и неопределённый интеграл. Таблица основных интегралов.
31. Свойства неопределённого интеграла. Непосредственное интегрирование. Примеры.
32. Интегрирование подстановкой. Примеры.
33. Интегрирование по частям. Примеры.
34. Интегрирование рациональных и иррациональных функций. Примеры.
35. Интегрирование тригонометрических функций. Примеры.
36. Определённый интеграл. Свойства определённого интеграла.
37. Вычисление определённого интеграла методом подстановки. Примеры.
38. Вычисление определённого интеграла по частям. Примеры.
39. Несобственные интегралы. Примеры.
40. Решение геометрических задач с помощью определённого интеграла. Примеры.
41. Решение технических задач с помощью определённого интеграла. Примеры.
В билет войдут два вопроса и две задачи по указанным темам






