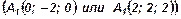45. Через вершину конуса проведено сечение под углом 30° к высоте конуса. Вычислить площадь сечения, если высота конуса равна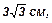 
а радиус основания равен 5 см. (24 см2).
46. Через образующую цилиндра проведено два сечения, из которых одно осевое. Площадь меньшего из сечений равна Q. Угол между плоскостями сечений равен 60°. Найти площадь осевого сечения.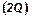 
47. Найти радиус шара, объем которого равен объему тела, образованного вращением равнобедренного прямоугольного треугольника вокруг гипотенузы, длина которой равна 2а. 
Длины окружностей оснований усеченного конуса равны 4p и 10p. Высота конуса равна 4. Найти площадь поверхности усеченного конуса. (64p).
49. Известно, что две взаимно перпендикулярные образующие конуса делят окружность его основания на дуги 120° и 240°. Найти объем конуса, если его высота равна Н. 
50. В конус вписан шар. Найти объем шара, если образующая конуса равна ℓ и наклонена к основанию под углом a.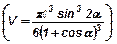 
51. Равнобедренный треугольник, у которого основание равно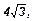 
а угол при вершине 120°, вращается вокруг прямой, содержащей основание. Найти площадь поверхности тела вращения. (16p).
52. Объем конуса равен V. Высота его разделена на три равные части, и через точки деления проведены плоскости, параллельные основанию. Найти объем средней отсеченной части.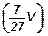 
53. В конус, осевое сечение которого есть равносторонний треугольник, вписан шар радиуса r = 2 см. Найти объем конуса. (24p см3).
54. В конус с радиусом основания 2 см вписан шар радиуса 1 см. Найти объем конуса.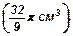 
Найти полную поверхность цилиндра, в осевом сечении которого квадрат, если его боковая поверхность равна 80. (120).
56. Центральный угол в развертке боковой поверхности конуса равен 120°. Площадь боковой поверхности конуса равна 12p. Найти площадь осевого сечения конуса.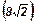 
.
57. Образующая усеченного конуса равна ℓ и составляет с плоскостью основания угол a. Диагональ его осевого сечения перпендикулярна образующей. Найти площадь боковой поверхности конуса.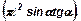 
.
Диагонали ромба равны 6 и 8. Этот ромб вращается вокруг прямой, содержащей одну из его сторон. Найти площадь поверхности полученного тела. (96p).
Сечения шара двумя параллельными плоскостями, между которыми лежит центр шара, имеют площади 144p и 25p. Найти площадь поверхности шара, если расстояние между параллельными плоскостями равно 17. (676p).
Сечения сферы двумя параллельными плоскостями имеют длины 10p и 24p. Найти площадь сферы, если расстояние между плоскостями равно 7 и центры сечений лежат на одном радиусе. (676p).
61. Высота усеченного конуса равна 5, а диагональ осевого сечения - 13. Радиусы оснований относятся как 1:2. Найти объем конуса.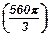 
62. В равнобедренном треугольнике АВС АВ = ВС = 10, АС = 12. Треугольник вращается вокруг оси, проходящей через вершину С и перпендикулярной АС. Найти объем тела вращения. (576p).
63. Угол в развертке боковой поверхности конуса равен 120°. Площадь боковой поверхности конуса равна 3p. Найти объем конуса.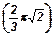 
64. Сечение цилиндра, параллельное его оси, отсекает от окружности основания дугу 120°. Радиус основания цилиндра равен R, а угол между диагональю сечения и осью цилиндра равен 30°. Найти объем цилиндра.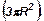 
65. Плоскость, параллельная оси цилиндра, отстоит от нее на расстояние, равное 15. Диагональ получившегося сечения равна 20, а радиус основания цилиндра равен 17. Найти объем цилиндра. 
66. Радиус основания конуса равен 4, а его высота - 10. В этот конус вписан цилиндр так, что его верхнее основание касается боковой поверхности конуса, а нижнее лежит в плоскости его основания. Осевое сечение цилиндра - квадрат. Найти объем цилиндра.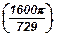 
67. Через точку, не лежащую на сфере, проведены две плоскости, касающиеся сферы. Найти расстояние от центра сферы до линии пересечения плоскостей, если угол между плоскостями равен 60°, а площадь сферы 32p.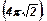 
68. Через точку на поверхности шара проведены две плоскости, пересекающие его. Обе плоскости удалены от центра сферы на расстояние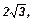 
угол между ними равен 60°. Найти площади получившихся сечений. 
69. Два цилиндра, радиусы которых относятся как 2:3, имеют равные объемы. Найти отношение площадей боковых поверхностей данных цилиндров.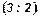 
70. Из круга вырезан сектор, представляющий собой четверть круга. Из этого сектора и из оставшейся части круга изготовлены боковые поверхности двух конусов. Найти отношение высот этих конусов.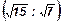 
На гранях двугранного угла взяты две точки, удаленные от ребра двугранного угла на 6 см и 10 см. Известно, что одна из этих точек удалена от второй грани на 7,5 см. Найти расстояние от второй точки до противоположной грани двугранного угла. (4,5 см).
72. Через сторону ромба ABCD проведена плоскость a. Сторона АВ составляет с этой плоскостью угол 30°. Найти угол между плоскостью ромба и плоскостью a, если острый угол ромба равен 45°. (45°).
73. Из точки М к плоскости a проведены две наклонные, которые образуют со своими проекциями на плоскость a углы 30°. Угол между наклонными равен 90°. Найти расстояние между основаниями наклонных, если расстояние от точки М до плоскости a равен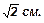 
(4 см).
74. Плоскости a и b параллельны. Из точки М (плоскости a и b расположены по одну сторону от точки М) проведены две прямые. Первая прямая пересекает плоскости a и b соответственно в точках А и В, а вторая прямая - в точках С и D, причем AM = CD, MC = 16, AB = 25. Расстояние от точки М до плоскости a равно 12. Найти расстояние между плоскостями. (15).
75. Точка М расположена между параллельными плоскостями a и b. Через точку М проведены две прямые. Первая прямая пересекает плоскость a в точке А, а плоскость b - в точке В. Вторая прямая пересекает эти плоскости соответственно в точках С и D; МA = МD, MC = 32, МB = 50. Расстояние от точки М до плоскости a равно 24. Найти расстояние между плоскостями. (54).
76. В треугольнике АВС АВ = ВС = 25, АС = 48, BD - перпендикуляр к плоскости АВС. BD =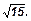 
Найти расстояние от точки D до прямой АС. (8).
77. ABCD - ромб со стороной, равной а, ÐА = 60°, АМ^АВС, АМ = 0,5а. Найти расстояние от точки М до прямой СD. (a).
78. треугольнике АВС АC = BC = m, ÐАCD = 120°, РА^АВС. Точка Р удалена на расстояние, равное m, от прямой ВС. Найти расстояние от точки Р до плоскости АВС.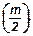 
Точка М удалена от каждой стороны равнобедренной трапеции на расстояние, равное 12 см. Основания трапеции равны 18 см и 32 см. Найти расстояние от точки М до плоскости трапеции. (0).
80. Средняя линия прямоугольной трапеции равна 6. Острый угол трапеции равен 30°. Точка М удалена от плоскости трапеции на расстояние, равное 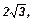и находится на равном расстоянии от ее сторон. Найти расстояние от точки М до сторон трапеции. (0).
81. Через середину отрезка с концами в точках Р(-1; 2; 5) и Q(3; -4; 1) проведена плоскость, перпендикулярная прямой, проходящей через точки А (0; -2; -1) и В (3; 2; -1). Составить уравнение плоскости. (3x + 4y +1 = 0).
82. Высота АА1 прямоугольного параллелепипеда ABCDA1B1C1D1 вдвое больше каждой из сторон основания. Найти угол между прямыми BD1 и АМ, где М - точка пересечения диагоналей грани DСC1D1.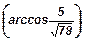 
83. Дан куб ABCDA1B1C1D1; точка К - середина ребра AA1, L - центр грани CC1D1D. Найти угол между плоскостями BKL и АD1С.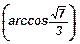 
84. Дан прямоугольный параллелепипед ABCDA1B1C1D1, в котором АВ = 4, AD = 6, AA1 = 2. Точки F и K расположены на ребрах AD и B1C1 соответственно, причем AF:FD = C1K:KB1 = 1:2, P - точка пересечения диагоналей грани ABCD. Найти угол между прямыми PK и B1F.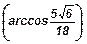 
85. Дан тетраэдр ABCD. Все плоские углы при вершине D - прямые; DA = 1, DB = 2, DC = 3. Найти медиану тетраэдра, проведенную из вершины D.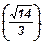 
86. Даны точки А (1; 0; 1), В (-2; 2; 1), С (2; 0; 3) и D (0; 4; -2). Найти уравнение плоскости, проходящей через точку D параллельно плоскости АВС. (2x + 3y - z - 14 = 0).
87. Найти площадь сечения куба ABCDA1B1C1D1 плоскостью, проходящей через вершину А и середины ребер B1C1 и C1D1, если ребро куба равно а.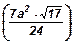 
88. Дан равнобедренный треугольник АВС (АС = СВ). А (1; -2; 1), В (3; 2; -3). Вершина С лежит на оси ординат. Найти площадь треугольника АВС. (9).
89. В правильной четырехугольной призме ABCDA1B1C1D1 сторона основания равна 2, а боковое ребро - 4. Е - середина CD и K - середина C1С. DK пересекает D1C в точке Р. Найти расстояние между серединой М отрезка B1Е и точкой Р.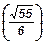 
90. Точки А (1; 1; 5), В (4; 7; 5), С (8; 5; 5), D (5; -1; 5) являются вершинами прямоугольника АВСD. Найти больший угол между диагоналями прямоугольника.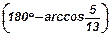 
91. (Л4, № 14.76.50). В параллелограмме АВСD известны координаты трех вершин А (3; 1; 2), В (0; -1; -1), С (-1; 1; 0). Найти длину диагонали BD.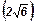 
CV 92. (Л4, № 14.76.51). Доказать, что точки А (1; -1; 1), В (1; 3; 1), С (4; 3; 1), D (4; -1; 1) являются вершинами прямоугольника. Вычислить длины его диагоналей и координаты точки их пересечения.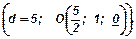 
93. Вершинами треугольника являются точки А(2; -3; 0), В(2; -1; 1), С(0; 1; 4). Найти величину угла, образуемого медианой ВD и основанием АС. (45°)
94. Треугольная пирамида задана вершинами А(3; 0; 1), В(-1; 4; 1), С(5; 2; 3), D(0; -5; 4). Вычислить длину вектора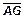 
, если G - точка пересечения медиан грани BCD.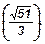 
95. Объем прямой треугольной призмы ABCA1B1C1 равен 3. Определить координаты вершины A1, если координаты вершин одного из оснований призмы известны: А (1; 0; 1), В (2; 0; 0), С (0; 1; 0). 
