ЗАДАЧИ К ЭКЗАМЕНУ ПО ГЕОМЕТРИИ. 10 класс.
1. Угол между противоположными ребрами АВ и CD пирамиды ABCD равен a, АВ = а, CD = b. Найдите площадь сечения этой пирамиды плоскостью, проходящей через середину ребра ВС параллельно прямым АВ и CD. 
2. Объем правильной четырехугольной пирамиды равен V. Угол наклона ее бокового ребра к плоскости основания равен a. Найти боковое ребро пирамиды. 
В пирамиде ABCF через медиану BK основания АВС и середину L бокового ребра AF проведена плоскость. Найти отношение объема многогранника BCKLF к объему пирамиды АBKL. (3).
4. Основанием четырехугольной пирамиды служит квадрат. Одно из боковых ребер перпендикулярно плоскости основания, два других наклонены к основанию под углом 60°. Найти полную поверхность пирамиды, если сторона квадрата равна 4. 
5. Угол между боковой гранью и плоскостью основания правильной треугольной пирамиды равен 45°. Объем пирамиды равен 
Найти длину стороны основания пирамиды. (2).
6. В правильной треугольной пирамиде известны высота Н и величина двугранного угла 2a, образованного боковыми гранями. Найти длину стороны основания. 
7. Найти двугранный угол между боковыми гранями правильной треугольной пирамиды, если двугранный угол, образуемый боковой гранью с основанием, равен a. 
8. Основанием пирамиды SABCD является прямоугольник ABCD со сторонами 
и а. Ребро SC перпендикулярно к плоскости основания, а ребро SA образует с ней угол a. Найти площадь сечения пирамиды плоскостью, параллельной прямой SA и проходящей через BD. 
9. Отрезок прямой, соединяющей центр основания правильной треугольной пирамиды с серединой бокового ребра, равен стороне основания. Найти угол между смежными боковыми гранями пирамиды. 
10. Основанием пирамиды служит равнобедренная трапеция, основания которой равны 2 см и 8 см. Боковые грани наклонены к основанию под углом 60°. Найти высоту пирамиды и площадь ее боковой поверхности. 
11. В основании пирамиды лежит ромб со стороной, равной а, и углом 60°. Боковые грани, проходящие через стороны острого угла ромба, перпендикулярны плоскости основания, а остальные две боковые грани наклонены к плоскости основания под углом 60°. Найти площадь боковой поверхности пирамиды. 
12. В основании пирамиды DАВС лежит треугольник ABC, у которого АC = = ВС = a, ÐACB = 120°. Грани DАС и DАВ перпендикулярны к плоскости основания, а грань DВС составляет с ней угол 45°. Найти площадь боковой поверхности пирамиды. 
13. В правильной треугольной пирамиде боковые грани наклонены к плоскости основания под углом 60°. Расстояние от вершины основания до боковой грани равно 
Найти площадь боковой поверхности пирамиды. 
14. В правильной четырехугольной пирамиде сторона основания равна 4 см, а расстояние от центра основания до бокового ребра равно 2 см. Найти угол между смежными боковыми гранями и плоский угол при вершине пирамиды. 
15. В правильной треугольной усеченной пирамиде стороны оснований равны 6 см и 8 см, а боковые грани наклонены к плоскости основания под углом 60°. Найти площадь боковой поверхности пирамиды. 
16. В правильной четырехугольной усеченной пирамиде стороны оснований равны 6 см и 8 см, а боковые грани наклонены к плоскости основания под углом 45°. Найти площадь боковой поверхности пирамиды.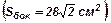 
17. В правильной треугольной пирамиде высота основания равна h, боковые ребра наклонены к плоскости основания под углом a. Найти объем пирамиды. 
18. В правильной четырехугольной пирамиде диагональ основания равна d. Боковые грани наклонены к плоскости основания под углом a. Найти объем пирамиды. 
19. Стороны оснований правильной четырехугольной усеченной пирамиды равны 
и 
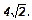Площадь диагонального сечения равна 90. Найти объем пирамиды.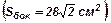
20. Центр грани куба с ребром а соединен с серединами сторон противоположной грани, которые также соединены в последовательном порядке. Вычислить площадь поверхности пирамиды, ребрами которой являются проведенные отрезки. 
Боковые грани правильной треугольной призмы - квадраты. Площадь боковой поверхности призмы равна 144. Найти объем многогранника, вершинами которого служат центры всех граней призмы. (12).
22. В кубе ABCDA1B1C1D1 c ребром длины а точка K - середина ребра AB, точка Е - середина ребра DD1. Найти периметр треугольника A1KЕ и определить, в каком отношении делит объем куба плоскость, проходящая через вершины этого треугольника.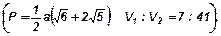 
23. В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро АВ = а, ВС = а, AA1 = b, причем а > b. Найти площадь сечения, проходящего через вершину А и перпендикулярного диагонали BD1. 
24. В правильной треугольной призме через сторону нижнего основания и середину противоположного ребра проведена плоскость, образующая с плоскостью основания угол 60°. Площадь сечения равна 
Найти объем и полную поверхность призмы. 
25. Основанием наклонного параллелепипеда служит ромб ABCD со стороной а и острым углом a. Ребро АA1 равно b и образует с ребрами АВ и AD угол j. Найти объем параллелепипеда. 
26. В прямой треугольной призме через одну из сторон нижнего основания проведена плоскость, пересекающая противоположное боковое ребро и составляющая с плоскостью основания угол, равный 45°. Определить площадь сечения, если в основании призмы лежит правильный треугольник, сторона которого равна а. 
27. В прямой призме ABCA1B1C1 АВ = 13, ВС = 21, АС = 20. Диагональ боковой грани A1C составляет с плоскостью грани CC1B1B угол 30°. Найти площадь полной поверхности призмы. 
28. В основании прямой призмы лежит параллелограмм, через сторону которого, равную а, и противоположную ей сторону верхнего основания проведено сечение, составляющее с плоскостью основания угол b; площадь сечения Q. Найти объем призмы. 
29. В правильной треугольной призме ABCA1B1C1 сторона основания равна 4 см. Через середину A1C1 и сторону основания ВС проведена плоскость. Найти площадь сечения, если длина бокового ребра равна 2 см.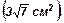 
30. В прямом параллелепипеде ABCDA1B1C1D1 основанием служит ромб со стороной, равной а, ÐВAD = 60°. Через сторону AD и вершину В1 проведена плоскость, составляющая с плоскостью основания угол 45°. Найти длину бокового ребра и площадь сечения. 
31. В прямом параллелепипеде ABCDA1B1C1D1 АВ = 1, ВС = 
ÐАВС = 150°. Через диагональ AС и вершину В1 проведена плоскость, составляющая с плоскостью основания угол в 60°. Найти площадь боковой поверхности. 
32. Высота правильной четырехугольной призмы равна h. Из одной вершины основания проведены в двух смежных боковых гранях две диагонали, угол между которыми равен a. Определить боковую поверхность призмы. 
33. В наклонной треугольной призме площади двух граней равны 70 см2 и 105 см2, угол между ними 60°. Боковое ребро равно 10 см. Найти площадь боковой поверхности призмы. 
34. Основанием прямоугольного параллелепипеда служит квадрат. Диагональ параллелепипеда равна d и составляет с боковой гранью угол 30°. Найти объем параллелепипеда. 
35. Основанием прямой призмы ABCA1B1C1 служит прямоугольный треугольник АВС (ÐС = 90°). АС = 4; ВС = 
Ð AB1C = 30°. Найти объем призмы. 
36. В основании прямого параллелепипеда лежит ромб, диагонали которого равны 6 и 8. Плоскость сечения, проходящего через два противоположных ребра верхнего и нижнего оснований, составляет с основанием угол 60°. Найти объем параллелепипеда. 
37. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 диагонали B1F и B1E равны соответственно 24 и 25. Найти объем призмы.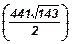 
38. Основанием наклонной призмы служит правильный треугольник. Одна из боковых граней является ромбом с диагоналями, равными 6 и 8. Боковые ребра наклонены к основанию под углом 60°. Найти объем призмы. 
39. В наклонном параллелепипеде ABCDA1B1C1D1 боковое ребро равно 10. Расстояния от ребра AA1 до ребер BВ1 и DD1 равны соответственно 5 и 12, а расстояние между ребрами АА1 и СС1 равно 13. Найти объем параллелепипеда. (600).
40. Стороны основания прямоугольного параллелепипеда равны 6 и 8. Через диагональ основания проведена плоскость, параллельная диагонали параллелепипеда. Эта плоскость составляет с плоскостью основания угол 45°. Найти объем параллелепипеда. (460,8).
41. Стороны треугольника a = b = 10 см, с = 12 см касаются сферы радиуса 5 см. Найти расстояние от центра сферы до плоскости треугольника. (4 см).
42. В конус вписан шар, поверхность которого равна площади основания конуса. Найти косинус угла при вершине в осевом сечении конуса. 
43. Осевое сечение конуса - равносторонний треугольник. Найти отношение объема конуса к объему вписанного в него шара. 
