Вибираємо матеріал із середніми механічними характеристиками (стор.34, табл.3.3):
- для шестерні – сталь 45 (покращена), НВ230;
- для колеса зубчатого – сталь 45 (покращена), НВ200.
Розраховуємо допустиме контактне напруження:
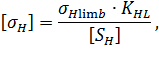
де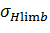 
– границя контактної витривалості (стор.34, табл.3.2);
– коефіцієнт довговічності, при довготривалій експлуатації редуктора приймають, 
;
– коефіцієнт безпеки, приймають 
(стор.33).
Визначаємо границя контактної витривалості:
,
де 
– числове значення твердості поверхонь зубів.
Отже розрахункове допустиме контактне напруження становитиме:
- для шестерні:
МПа
- для колеса зубчатого:
МПа
Загальне допустиме контактне напруження для зубчатої передачі становить:
МПа
Приймаємо коефіцієнт нерівномірного розподілення навантаження по довжині контактних ліній: 
(стор.32, табл.3.1), та приймаємо коефіцієнт ширини вінця 
в залежності від виду циліндричної передачі:
− для циліндричної прямозубої передачі: 
(приймаємо 
);
− для циліндричної косозубої передачі: 
(приймаємо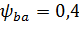 
);
− для циліндричної шевронної передачі: 
(приймаємо 
).
Визначаємо міжвісеву відстань із умови дотичної витривалості:
,
де 
– коефіцієнт міжвісевої відстані:
− для циліндричної прямозубої передачі: 
;
− для циліндричної косозубої або шевронної передач: 
;
– передаточне число зубчатої передачі;
– крутний момент на вихідному валу зубчатого редуктора;
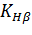– коефіцієнт нерівномірного розподілення навантаження по довжині контактних ліній;
– загальне допустиме контактне напруження;
- коефіцієнт ширини вінця.
Отже, міжвісева відстань становитиме:
мм
приймаємо ближче стандартне значення по ГОСТ 9563-60: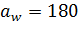 
мм (стор.36).
Розраховуємо номінальний модуль:
мм
приймаємо стандартне значення по ГОСТ 9563-60: 
мм (стор.36).
Приймаємо кут нахилу зубів 
:
− для циліндричної прямозубої передачі: 
(приймаємо );
− для циліндричної косозубої передачі: 
(приймаємо 
);
− для циліндричної шевронної передачі: 
(приймаємо 
);
Визначаємо сумарне число зубів шестерні та колеса циліндричної прямозубої передачі:
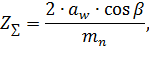
де 
– прийнята міжвісева відстань;
– кут нахилу зуба;
– прийнятий номінальний модуль.
Виходячи з розрахункового значення сумарного числа зубів, можна визначити число зубів окремо для шестерні 
та колеса зубчатого 
:
де 
– сумарне число зубів шестерні та колеса;
– передаточне число зубчатої передачі.
Визначаємо число зубів шестерні циліндричної косозубої або шевронної передач:
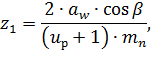
де – прийнята міжвісева відстань;
– кут нахилу зуба;
– передаточне число зубчатої передачі;
– прийнятий номінальний модуль.
Отже, число зубів шестерні становить:
;
приймаємо ціле число, округлюючи до ближчого значення: 
;
Визначаємо число зубів колеса зубчатого циліндричної косозубої або шевронної передач:
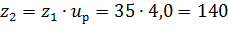
приймаємо ціле число, округлюючи до ближчого значення: 
.
Уточнюємо значення кута нахилу зубів:
отже уточнюючий кут нахилу зубів становитиме: 
.
Визначаємо основні розміри шестерні та зубчатого колеса:
- ділильні діаметри циліндричної прямозубої передачі:
,
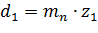
де – прийнятий номінальний модуль;
та – прийняте число зубів шестерні та колеса зубчатого.
− ділильні діаметри циліндричної косозубої або шевронної передач:
мм;
мм
− перевірка міжвісевої відстані:
мм
- діаметри вершин зубів шестерні та зубчатого колеса для всіх видів циліндричних передач:
мм;
мм
- діаметри западин зубів шестерні та зубчатого колеса для всіх видів циліндричних передач:
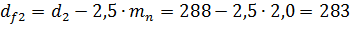мм;
мм
- ширина зубчатого колеса для всіх видів циліндричних передач:
мм
приймаємо ближче стандартне значення по ГОСТ 9563-60: 
мм (стор.161÷162).
- ширина шестерні для всіх видів циліндричних передач:
мм
Визначаємо коефіцієнт ширини шестерні по діаметру:
Визначаємо колову швидкість коліс та степінь точності передачі:
м/с
при такій коловій швидкості приймаємо 8-му степінь точності передачі. (стор.32)
Розраховуємо загальний коефіцієнт, який враховує нерівномірний розподіл навантаження по ширині вінця та між зубцями передачі, а також динамічне навантаження:
де 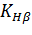– коефіцієнт нерівномірного розподілу навантаження по ширині вінця [таб.3.5]: 
;
– коефіцієнт нерівномірного розподілу навантаження між зубцями передачі [таб.3.4]: 
;
– коефіцієнт динамічного навантаження [таб.3.6]: 
.
Отже, загальний коефіцієнт становитиме:
Розраховуємо перевірку контактних напружень циліндричної прямозубої передачі:
Розраховуємо перевірку контактних напружень циліндричної косозубої або шевронної передач:
,
де – прийнята міжвісева відстань;
– крутний момент на вихідному валу зубчатого редуктора;
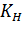– загальний коефіцієнт;
– прийнята ширина зубчатого колеса;
– передаточне число зубчатої передачі;
– загальне допустиме контактне напруження.
Отже, перевірка контактних напружень становитиме:
Розраховуємо сили, які діють в зачепленні циліндричної зубчатої передачі (роз'яснення див. стор.158-159):
- колова сила:
Н
- радіальна сила:
Н
− вісева сила:
H
Перевіряємо міцність зубів на витривалість по напруженням згину циліндричної прямозубої передачі:
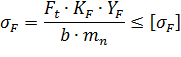
Перевіряємо міцність зубів на витривалість по напруженням згину циліндричної косозубої або шевронної передач:
де 
– розрахункова колова сила;
KF – коефіцієнт навантаження;
– коефіцієнт, який враховує форму зуба (роз'яснення див. стор.42);
– коефіцієнт, який введений для компенсації похибки;
– коефіцієнт нерівномірного розподілу навантаження між зубцями передачі;
– прийнята ширина зубчатого колеса;
– прийнятий номінальний модуль.
Розраховуємо коефіцієнт навантаження:
де 
– коефіцієнт, який враховує нерівномірність розподілу навантаження по довжині зуба [таб.3.7]: 
;
– коефіцієнт динамічного навантаження [таб.3.8]: 
.
Отже, коефіцієнт навантаження становитиме:
Розраховуємо коефіцієнти, які враховують форму зубів та залежить від еквівалентного числа зубів 
:
- для шестерні:
- для зубчатого колеса:
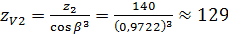
тоді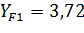 
та 
приймається розрахунковим методом інтерполяції (стор.42).
Розраховуємо допустиме напруження:
де 
– значення границі витривалості при нульовому циклі згину (стор.43÷45, таб.3.9);
– коефіцієнт безпеки:
де 
– коефіцієнт, який враховує нестабільність матеріалу зубчатих коліс (стор.43÷45, таб.3.9);
– коефіцієнт, який враховує спосіб отримання заготовки зубчатого колеса (стор.44).
Отже, коефіцієнт безпеки становить:
Отже, розрахункове допустиме напруження становить:
- для шестерні:
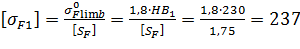МПа
- для зубчатого колеса:
МПа
Знаходимо співвідношення:
- для шестерні: 
МПа
- для колеса: 
МПа
В подальшому розрахунок слід вести для зубів колеса, у якого знайдене менше співвідношення.
Визначаємо коефіцієнт, який введений для компенсації похибки :
Приймаємо коефіцієнт нерівномірного розподілу навантаження між зубцями передачі: 
(приймається середнє значення для розрахунку курсового проекту).
Отже, міцність зубів на витривалість по напруженням згину зубчатого колеса становить:
Умова виконана.
