Нулевая гипотеза: Генеральная совокупность, из которой извлечена выборка, распределена по нормальному закону. (Н0: Х 
Основная гипотеза (Н0: Х 
, которую мы проверим с помощью критерия Пирсона 
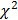
Вероятности рассчитываются с помощью функции Лапласа Ф(y):
P1= P(-∞ < y < 14,5) = 
P2= P(14,5 < y < 17,5) = 
=0,0045
P3= P(17,5 < y < 20,5) =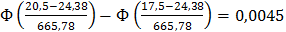 
P4= P(20,5 < y < 23,5) =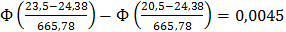 
P5= P(23,5 < y < 26,5) = 
P6= P(26,5 < y < 29,5) = 
P7= P(29,5 < y < 32,5) =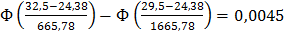 
P8= P(32,5 < y < 35,5) = 
0,0045
P9= P(35,5 < y < ∞) = 
Таблица 3
Расчетная таблица для вычисления 
| Интервалы (a(i);a(i+1)] | Частоты эмпирические n(i) | Вероятности P(i) | Теоретические частоты 
| 
|
| (-∞;25,5] | 0,10027 | 10,027 | 0,409767 | |
| (25,5;26,5] | 0,18747 | 18,747 | 1,471916 | |
| (26,5;27,5] | 0,27188 | 27,188 | 0,051911 | |
| (27,5;28,5] | 0,24549 | 24,549 | 0,008286 | |
| (28,5;29,5] | 0,13784 | 13,784 | 1,038788 | |
| (29,5;30,5] | 0,04604 | 4,604 | 0,079239 | |
| (30,5;∞) | 0,01101 | 1,101 | 3,275387 | |
| Sum | 6,335293 |
= 6,335293
Для определения критических точек распределения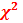 
необходимо знать уровень значимости(
и число степеней свободы(
.
S – число интервалов = 9, r – число параметров = 2. 
6)=6,05
Т.к. 
, то считаем, что нет оснований для отклонения нулевой гипотезы при заданном уровне значимости 
.
Рисунок 3. График эмпирической функции f(y)
В случае принятия гипотезы найти интервальные оценки параметров нормального закона распределения (доверительную вероятность принять равной 0,95).
0.2782
27.29 - 0.2782 < 
< 27.29 + 0.2782
27.0118 < 
< 27.5682 – доверительный интервал математического ожидания Y
- доверительный интервал среднего квадратического отклонения
9. Провести корреляционный анализ:
А) Составить корреляционную таблицу;
Б) Найти выборочный коэффициент корреляции;
в) Проверить значимость выборочного коэффициента корреляции при
α = 0,05(Н0: ρ = 0), при альтернативной гипотезе Нα: ρ ≠ 0;
г) Построить корреляционное поле и по характеру расположения точек на нём подобрать общий вид функции регрессии;
Д) Найти эмпирические функции регрессии Y на X, X на Y и построить их графики.
Таблица 4
А) Корреляционная таблица эмпирического распределения двумерной
СВ(X,Y)
| X\Y | n(x) | |||||||
| n(y) | n=100 |
Б) X = 128,8; Y = 27,29; Sx = 1,51; Sy = 1,4021.
Корреляционный момент:
Выборочный коэффициент корреляции:
В) Проверим значимость выбранного коэффициента корреляции.
Нулевая гипотеза:
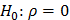
Альтернативная гипотеза:
13,97
Т.к. 
> 
, то нулевая гипотеза отвергается и коэффициент корреляции можно считать существенным, а связь между случайными величинами достоверной. Можно считать что между СВ Х и СВ Y существует корреляционная зависимость.
Г)
| Х |
| Y |
| Xy |
| Yx |
РИС. 4 Корреляционное поле и линии регрессии
Д) Выборочное уравнение регрессии Y на X:
Выборочное уравнение регрессии Х на Y:
Контроль вычислений: 0,88 * 0,76 = 0,6688 = 
Графики найденных выборочных функций нанесены на рис. 4.
