1. Информационные процессы в медицине рассматривает:
a) Медицинская информатика
b) Медицинская кибернентика
c) Информатика
d) Медицинская статистика
2. Обектом изучения медицинской информатики являются:
a) информационные технологии, реализуемые в здравоохранении
b) информационные процессы, сопряженные с медицинскими проблемами
c) оптимизация информационных процессов в медицине
d) нет правильного ответа
3. Основной целью медицинской информатики является:
a) оптимизация информационных процессов в медицине с помощью компьютерных
технологий
b) изучение информационных процессов в медицине
c) внедрение компьютерных технологий в медицину
d) нет правильного ответа
4. Программы обеспечивающие взаимодействие с аппаратными средствами
относятся к
a) базовому уровню
b) системному уровню
c) служебному уровню
d) прикладному уровню
5. Программы обеспечивающие взаимодействие всех программ с
программами базового уровня относятся к
a) базовому уровню
b) системному уровню
c) служебному уровню
d) прикладному уровню
6. Программы обеспечивающие взаимодействие с пользователем средствами
пользовательского интерфейса относятся к
a) базовому уровню
b) системному уровню
c) служебному уровню
d) прикладному уровню
7. Программы обеспечивающие автоматизацию работ по проверке, наладке и
настройке компьютерной системы относятся к
a) базовому уровню
b) системному уровню
c) служебному уровню
d) прикладному уровню
8. Программы обеспечивающие непосредственное выполнение необходимых
пользователю задач относятся к
a) базовому уровню
b) системному уровню
c) служебному уровню
d) прикладному уровню
9. Компьютерный анализ медицинских данных это:
a) математическое преобразование данных с помощью программных средств
b) математическая обработка медицинских данных
c) статистическая обработка медицинских данных
d) нет правильного ответа
10. Компьютерный анализ данных НЕ включает в себя следующий раздел:
a) предварительный анализ данных
b) планирование исследования
c) получение представления об основных статистических методах
d) интерпретация результатов
11. Какой из этапов анализа данных выполняется в первую очередь:
a) подготовка данных к анализу
b) предварительный анализ данных
c) выбор метода анализа
d) интерпретация результатов
12. Этап приведения данных к виду, позволяющему провести последующую
их обработку называется:
a) планирование исследования
b) подготовка данных к анализу
c) предварительный анализ данных
d) разведовательный анализ данных
13. Выявление вероятностных законов распределения, которым подчиняются
данные проводится на этапе:
a) планирование исследования
b) подготовка данных к анализу
c) предварительный анализ данных
d) реализация метода анализа данных
14. Выявление различий между группами данных проводится на этапе:
a) планирование исследования
b) подготовки данных к анализу
c) разведовательный анализ данных
d) интерпретация результатов
15. Непосредственный ввод исходных данных проводится на этапе:
a) планирования исследования
b) подготовки данных к анализу
c) предварительный анализ данных
d) разведовательный анализ данных
16. Определение взаимосвязей между переменными происходит на этапе:
a) планирования исследования
b) предварительного анализа данных
c) подготовка данных к анализу
d) интерпретации результатов
17. Пакет обработки данных Statistica относится к следующему типу:
a) специализированные пакеты
b) пакеты общего назначения
c) профессиональные пакеты
d) электронные таблицы
18. Рентгеновское изображение относится к следующему виду медицинской
информации:
a) алфавитно-цифровая
b) визуальная статическая
c) визуальная динамическая
d) комбинированная
19. Походка пациента, сухожильные рефлексы, реакция зрачка на свет
относятся к следующему виду медицинской информации:
a) алфавитно-цифровая
b) визуальная статическая
c) визуальная динамическая
d) комбинированная
20. Доплеровские сигналы кровотока при эхокардиографии относятся к
следующему виду медицинской информации:
a) алфавитно-цифровая
b) визуальная
c) звуковая
d) комбинированная
21. При телемедицинской консультации связь организуется по схеме:
a) точка - точка
b) много точек - точка
c) точка - много точек
d) много точек - много точек
22. При телемониторинге функциональных показателей связь организуется
по схеме:
a) точка - точка
b) много точек - точка
c) точка - много точек
d) много точек - много точек
23. При телемедицинской лекции / семинаре связь организуется по схеме:
a) точка - точка
b) много точек - точка
c) точка - много точек
d) много точек - много точек
24. При телемедицинском совещании связь организуется по схеме:
a) точка - точка
b) много точек - точка
c) точка - много точек
d) много точек - много точек
25. Дистанционное управление медицинской аппаратурой относится к:
a) телемедицинским консультациям
b) телемедицинским системам динамического наблюдения
c) телехирургии и дистанционному обследованию
d) телемедицине ургентных состояний
26. Дистанционное проведение лечебных воздействий, хирургических
операций относится к:
a) телемедицинским консультациям
b) телемедицинским системам динамического наблюдения
c) телехирургии и дистанционному обследованию
d) телемедицине ургентных состояний
27. Внедрение телемедицины в практику оказания неотложной медицинской
помощи относится к:
a) телемедицинским консультациям
b) телемедицинским системам динамического наблюдения
c) телехирургии и дистанционному обследованию
d) телемедицине ургентных состояний
28. Информационно-справочные системы относятся к медицинским
информационным системам
a) базового уровня
b) уровня лечебно-профилактических учреждений
c) территориального уровня
d) федерального уровня
29. Консультативно-диагностические системы относятся к медицинским
информационным системам
a) базового уровня
b) уровня лечебно-профилактических учреждений
c) территориального уровня
d) федерального уровня
30. Приборно-компьютерные системы относятся к медицинским
информационным системам
a) базового уровня
b) уровня лечебно-профилактических учреждений
c) территориального уровня
d) федерального уровня
31. Автоматизированные рабочие места специалистов относятся к
медицинским информационным системам
a) базового уровня
b) уровня лечебно-профилактических учреждений
c) территориального уровня
d) федерального уровня
32. Банки информации медицинских служб относятся к медицинским
информационным системам
a) базового уровня
b) уровня лечебно-профилактических учреждений
c) территориального уровня
d) федерального уровня
33. Персонифицированные регистры относятся к медицинским
информационным системам
a) базового уровня
b) уровня лечебно-профилактических учреждений
c) территориального уровня
d) федерального уровня
34. Скрининговые системы относятся к медицинским информационным
системам
a) базового уровня
b) уровня лечебно-профилактических учреждений
c) территориального уровня
d) федерального уровня
35. Информационные системы лечебно-профилактических учреждений
относятся к медицинским информационным системам
a) базового уровня
b) уровня лечебно-профилактических учреждений
c) территориального уровня
d) федерального уровня
36. Информационные системы НИИ и медицинских вузов относятся к
медицинским информационным системам
a) базового уровня
b) уровня лечебно-профилактических учреждений
c) территориального уровня
d) федерального уровня
37. Информационные системы территориального органа здравоохранения
относятся к медицинским информационным системам
a) базового уровня
b) уровня лечебно-профилактических учреждений
c) территориального уровня
d) федерального уровня
38. Информационные системы федерального органа здравоохранения
относятся к медицинским информационным системам
a) базового уровня
b) уровня лечебно-профилактических учреждений
c) территориального уровня
d) федерального уровня
39. Медицинские приборно-компьютерные системы для исследования
системы кровообращения относятся к
a) системам для проведения функциональных и морфологических исследований
b) мониторным системам
c) системам управления лечебным процессом
d) системам лабораторной диагностики
40. Медицинские приборно-компьютерные системы для ультрозвуковой
диагностики относятся к
a) системам для проведения функциональных и морфологических исследований
b) мониторным системам
c) системам управления лечебным процессом
d) системам лабораторной диагностики
41. Системы предназначенные для длительного непрерывного наблюдения за
состоянием пациента относятся к
a) системам для проведения функциональных и морфологических исследований
b) мониторным системам
c) системам управления лечебным процессом
d) системам лабораторной диагностики
42. Системы интенсивной терапии относятся к
a) системам для проведения функциональных и морфологических исследований
b) мониторным системам
c) системам управления лечебным процессом
d) системам лабораторной диагностики
43. Системы биологической обратной связи относятся к
a) системам для проведения функциональных и морфологических исследований
b) мониторным системам
c) системам управления лечебным процессом
d) системам лабораторной диагностики
44. Системы протезирования и искусственные органы относятся к
a) системам для проведения функциональных и морфологических исследований
b) мониторным системам
c) системам управления лечебным процессом
d) системам лабораторной диагностики
45. Что представляет собой гистограмма?
a) Это простой вариационный ряд
b) Это диаграмма, по оси ординат которой отложены относительные (абсолютные)
частоты попадания значений изучаемой величины в каждый классовый интервал, а
по оси абсцисс – границы классовых интервалов интервального вариационного ряда
c) Это график зависимости значений одной величины от другой
46. Как вычисляется относительная частота при построении гистограммы?
a) Делится значение варианты на ширину классового интервала
b) Делится среднее значение изучаемой величины в выборке на объём выборки
c) Делится число вариант в каждом классовом интервале на объём выборки
47. Для чего результаты эксперимента часто оформляют в виде гистограмм?
a) Для того чтобы оценить математическое ожидание изучаемой величины
b) Для того чтобы вычислить выборочные характеристики полученных
экспериментальных данных
c) Для того чтобы получить примерное представление о законе распределения значений
изучаемой величины в выборке
48. Почему необходимо иметь представление о законе распределения
значений изучаемой величины в выборке?
a) Знание закона распределения позволяет правильно выбрать метод статистического
анализа
b) Знание закона распределения позволяет вычислить выборочные характеристики
c) Знание закона распределения позволяет определить тип корреляционной взаимосвязи
между изучаемыми величинами
49. Если распределение в выборке соответствует нормальному закону
распределения, то какие методы статистического анализа можно
применять?
a) Только непараметрические
b) Только параметрические
c) И те и другие
d) Ни те ни другие
50. Применение каких методов статистического анализа предпочтительнее,
если распределение в выборке соответствует нормальному закону
распределения?
a) Параметрических
b) Непараметрических
c) И те и другие
d) Ни те ни другие
51. Применение каких методов статистического анализа является
правомерным, если распределение в выборке не соответствует нормальному
закону распределения?
a) Параметрических
b) Непараметрических
c) И те и другие
d) Ни те ни другие
52. Модой называется:
a) Наиболее часто встречающееся значение варианты
b) Значение варианты, которое делит вариационный ряд на две равные части
c) Величина, характеризующая сглаженность или остроконечность эмпирического
распределения по сравнению с нормальным распределением
d) Величина, характеризующая несимметричность эмпирического распределения
значений вариант относительно их среднего значения
53. В приведённом ряду чисел 5,6,7,7,7,8,9 какое число является модой?
a) 5
b) 7
c) 9
d) В этом примере мода отсутствует
54. В приведённом ряду чисел 5,6,7,7,7,8,9 какое число является медианой?
a) 5
b) 7
c) 9
d) В этом примере медиана отсутствует
55. Медианой называется:
a) Наиболее часто встречающееся значение варианты
b) Значение варианты, которое делит вариационный ряд на две равные части
c) Величина, характеризующая сглаженность или остроконечность эмпирического
распределения по сравнению с нормальным распределением
d) Величина, характеризующая несимметричность эмпирического распределения
значений вариант относительно их среднего значения
56. Эксцессом называется:
a) Наиболее часто встречающееся значение варианты
b) Значение варианты, которое делит вариационный ряд на две равные части
c) Величина, характеризующая сглаженность или остроконечность эмпирического
распределения по сравнению с нормальным распределением
d) Величина, характеризующая несимметричность эмпирического распределения
значений вариант относительно их среднего значения
57. Асимметрией называется:
a) Наиболее часто встречающееся значение варианты
b) Значение варианты, которое делит вариационный ряд на две равные части
c) Величина, характеризующая сглаженность или остроконечность эмпирического
распределения по сравнению с нормальным распределением
d) Величина, характеризующая несимметричность эмпирического распределения
значений вариант относительно их среднего значения
58. Какие статистические совокупности относятся к генеральным?
a) Если число членов совокупности n →∞
b) Если число членов совокупности ограничено
c) Если совокупность состоит только из дискретных величин
59. Какие статистические совокупности относятся к выборочным?
a) Если число членов совокупности n →∞
b) Если число членов совокупности ограничено
c) Если совокупность состоит только из дискретных величин
60. Числовые характеристики каких статистических совокупностей являются
случайными величинами?
a) Генеральных
b) Выборочных
c) Ни тех ни других
61. Числовые характеристики каких статистических совокупностей являются
детерминированными величинами?
a) Генеральных
b) Выборочных
c) Ни тех ни других
62. Числовые характеристики каких статистических совокупностей нельзя
найти экспериментально?
a) Генеральных
b) Выборочных
c) Ни тех ни других
63. Совпадают ли по значению выборочные характеристики с генеральными
параметрами?
a) Совпадают всегда
b) Совпадение может быть случайным
c) Не совпадают никогда
64. Какие из перечисленных числовых характеристик статистических
совокупностей относятся к генеральным совокупностям?
a) Среднее арифметическое, несмещённая дисперсия
b) Математическое ожидание, дисперсия
c) Средний квадрат отклонения
65. Какие из перечисленных числовых характеристик статистических
совокупностей являются выборочными характеристиками?
a) Среднее арифметическое, несмещённая дисперсия
b) Математическое ожидание
c) Дисперсия
66. Что является законом распределения для непрерывных случайных
величин?
a) Зависимость вероятности случайной величины от значения случайной величины
b) Зависимость плотности вероятности случайной величины от значения случайной
величины
c) Зависимость среднего выборочного значения от числа членов статистического ряда
67. Какое из определений относится к понятию «Математическое ожидание»?
a) Это наиболее вероятное значение случайной величины
b) Это среднее выборочное значение случайной величины
c) Это объём выборки
68. Какой смысл имеет выражение «Доверительный интервал для математического ожидания»?
a) Это диапазон изменения значений членов статистического ряда от максимального
значения случайной величины до минимального
b) Это такой интервал значений случайной величины, в котором находится
математическое ожидание с заданной вероятностью
c) Это такой интервал значений случайной величины, в котором находится выборочное
среднее с заданной вероятностью
69. Какая из перечисленных задач решается при статистическом анализе
данных?
a) Оценка неизвестных параметров генеральных совокупностей по известным
выборочным характеристикам
b) Оценка неизвестных выборочных характеристик по известным параметрам
генеральных совокупностей
c) Определение типа случайной величины – дискретная или непрерывная
70. Каким образом можно оценить надёжность (достоверность) полученных
выборочных характеристик?
a) Путём вычисления доверительной вероятности при заданных значениях
доверительных интервалов
b) Путём вычисления доверительных интервалов при заданном значении доверительной
вероятности
c) Путём вычисления выборочных характеристик
71. Достоверность найденных выборочных характеристик тем выше, чем:
a) Уже доверительные интервалы при высоком значении доверительной вероятности (
Рдов > 0,95)
b) Шире доверительные интервалы при невысоком значении доверительной
вероятности (Рдов< 0,95)
c) Надёжность выборочных характеристик не зависит от значения доверительных
интервалов
72. Какие числовые характеристики статистического ряда могут служить
признаками соответствия эмпирического распределения нормальному
закону распределения?
a) Все выборочные характеристики
b) Все генеральные параметры
c) Мода, Медиана, Эксцесс, Асимметрия
d) Математическое ожидание и дисперсия
73. Нормальный закон распределения непрерывных случайных величин в
общем виде описывается выражением:
a)f(x)= 
b) Y = A + B * X
c)f(x)=сигма* 
74. Нормальный закон распределения непрерывных случайных величин в
нормализованном виде (стандартизованном) виде описывается
выражением:
a) Y = A + B * t
b) f(x)=t* 
c)f(x)= 
75. При нормальном законе распределения все значения случайной величины
симметрично распределены относительно некоторого её значения. Как
называется это значение?
a) Дисперсия
b) Среднее квадратическое (стандартное) отклонение
c) Объём выборки
d) Математическое ожидание
76. При соответствии эмпирического распределения нормальному закону
какое соответствие между модой (Мо), медианой (Ме) и выборочным
средним (Х) является правильным?
a) Me < Mo < Х
b) Me + Mo = Х
c) Me = Mo = Х
d) Me ≠ Mo ≠ Х
77. Какие характеристики выборок являются точечными оценками
генеральных параметров?
a) Математическое ожидание, дисперсия, стандартное (среднее квадратическое)
отклонение
b) Все выборочные характеристики
c) Доверительные интервалы для соответствующих генеральных параметров
d) Закон распределения случайной величины в данной выборке
78. Каким образом осуществляется интервальная оценка генеральных
параметров?
a) Вычисляется ширина классовых интервалов по формуле Стерджеса
b) Вычисляется интервал изменения значений изучаемой величины
c) Вычисляются доверительные интервалы для соответствующих генеральных
параметров, при заданной доверительной вероятности
d) Вычисляется доверительная вероятность попадания значения изучаемой величины в
заданный доверительный интервал
79. Чему равны значения Эксцесса (Ех) и Асимметрии (As), если
эмпирическое распределение является строго нормальным распределением?
a) Ex = 0, As < 0
b) Ex = 0, As = 0
c) Ex > 0, As > 0
d) Ex и As могут принимать любые значения
80. При каких законах распределения вариант в выборке правомерно
применение критерия Стьюдента для интервальной оценки генеральных
параметров?
a) Если распределение соответствует биномиальному распределению
b) Если распределение соответствует нормальному закону
c) При любых законах распределения
d) Для интервальной оценки генеральных параметров критерий Стьюдента не
применяется
81. Какими параметрами полностью характеризуется нормальный закон
распределения?
a) Средним арифметическим эмпирического распределения
b) Математическим ожиданием и дисперсией
c) Объёмом выборки стандартным отклонением
d) Критериями Фишера и Стьюдента
82. Каким образом проверяется гипотеза о соответствии эмпирического
распределения нормальному закону методом теоретических частот?
a) Вычисленные теоретические частоты сопоставляются с численными значениями
вариант в выборке
b) Вычисленные теоретические частоты сопоставляются с эмпирическими частотами
интервального вариационного ряда
c) Значения теоретических частот, взятые из таблиц, сопоставляют с математическим
ожиданием
83. Каким образом проверяется гипотеза о соответствии эмпирического
распределения нормальному закону методом вычисления критерия
согласия X^2?
a) Вычисленное эмпирическое значение (X^2)эмп сопоставляется с критическим
значением (X^2)Крит, которое находят в соответствующей таблице
b) Вычисленное эмпирическое значение (X^2)эмп сопоставляется с выборочным
средним
c) Вычисленное эмпирическое значение (X^2)эмп сопоставляется с эмпирическими
частотами интервального вариационного ряда
84. Какое условие (из перечисленных) обязательно должно выполняться при
проверке гипотезы о соответствии эмпирического распределения
нормальному закону распределения методом критерия согласия X^2?
a) Выборочное среднее должно совпадать с математическим ожиданием
b) Объём выборки должен быть значительным (не менее 50)
c) Объём выборки должен быть незначительным(не более 50)
d) Дисперсия не должна превышать некоторого критического значения
85. Каким образом проверяется гипотеза о соответствии эмпирического
распределения нормальному закону методом вычисления Моды (Мо) и
Медианы (Ме)?
a) Вычисленные значения Мо и Ме сопоставляются друг с другом
b) Вычисленные значения Мо и Ме сопоставляются с выборочным средним
c) Вычисленные значения Мо и Ме сопоставляются с теоретическими, взятыми из
соответствующих таблиц
86. Каким образом проверяется гипотеза о соответствии эмпирического
распределения нормальному закону методом вычисления Эксцесса?
a) Вычисленное значение Эксцесса сопоставляется с Модой эмпирического ряда
b) Вычисленное значение Эксцесса сопоставляется с Медианой эмпирического ряда
c) Вычисленное значение Эксцесса сопоставляется с его критическим значением,
взятым из соответствующей таблицы при заданном уровне значимости
d) Вычисленное значение Эксцесса сопоставляется с критерием Стьюдента, взятым из
соответствующей таблицы при заданном уровне значимости
87. Каким образом проверяется гипотеза о соответствии эмпирического
распределения нормальному закону методом вычисления Асимметрии?
a) Вычисленное значение Асимметрии сопоставляется с Модой эмпирического ряда
b) Вычисленное значение Асимметрии сопоставляется с Медианой эмпирического
ряда
c) Вычисленное значение Асимметрии сопоставляется с её критическим значением,
взятым из соответствующей таблицы при заданном уровне значимости
d) Вычисленное значение Асимметрии сопоставляется с критерием Стьюдента, взятым
из соответствующей таблицы при заданном уровне значимости
88. На диаграмме изображены два графика нормального закона
распределения. Каким параметрами они отличаются?

a) Дисперсиями
b) Математическими ожиданиями
c) Математическими ожиданиями и дисперсиями
d) Критериями Стьюдента
e) Другими параметрами
89. На диаграмме изображены два графика нормального закона
распределения. Чему равны математические ожидания этих распределений?

a) 0 и 0,035
b) 20 и 20
c) -10 и 50
d) На диаграмме их значения не указаны
90. На диаграмме изображены два графика нормального закона
распределения. Чему равны математические ожидания этих распределений?
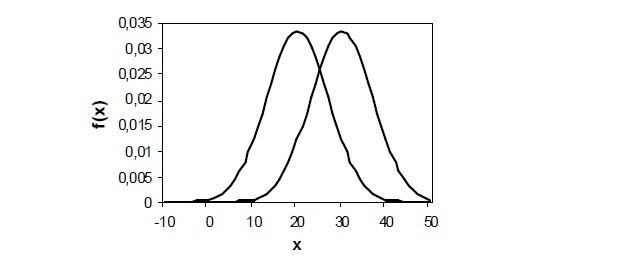
a) 0 и 0,035
b) 20 и 30
c) -10 и 50
d) На диаграмме их значения не указаны
91. На диаграмме изображены два графика нормального закона
распределения. Какими параметрами отличаются эти распределения?

a) Дисперсиями
b) Математическими ожиданиями
c) Критериями Стьюдента
d) Математическими ожиданиями и дисперсиями
e) Другими параметрами
92. Для каких генеральных параметров возможно вычисление доверительных
интервалов?
a) Только для математического ожидания
b) Только для дисперсии
c) Только для среднего квадратического (стандартного) отклонения
d) Для всех перечисленных
93. Каким образом вычисляются границы доверительного интервала + -å для математического ожидания, если эмпирическое распределение является нормальным, а объём выборки n > 30? (Sx - выборочное стандартное отклонение)
a)  , где t – нормализованный параметр нормального распределения
, где t – нормализованный параметр нормального распределения
b) 
с)  , где tNo - критерий Стьюдента
, где tNo - критерий Стьюдента
94. Каким образом вычисляются границы доверительного интервала }å для
математического ожидания, если эмпирическое распределение является
нормальным, а объём выборки n < 30? (Sx - выборочное стандартное отклонение)
a)  , где t – нормализованный параметр нормального распределения
, где t – нормализованный параметр нормального распределения
b) 
c)  , где где tNo - критерий Стьюдента
, где где tNo - критерий Стьюдента
95. Каким образом в математической статистике решается вопрос о различии
или совпадении двух выборок?
a) Путём сопоставления выборочных средних сравниваемых выборок
b) Путём нахождения вероятности различия выборок и сопоставления её значения с
заданным уровнем значимости
c) Путём вычисления математических ожиданий случайных величин в выборках и
сопоставления их значений
96. При решении вопроса о расхождении или совпадении двух выборок часто
пользуются таблицами критических значений критерия Стьюдента.
Использование этих таблиц является правомерным, если:
a) Обе выборки извлечены из генеральных совокупностей с нормальным законом
распределения и примерно одинаковыми дисперсиями
b) Эмпирические распределения значений вариант в выборках не соответствуют
нормальному закону распределения
c) Применения этих таблиц правомерно при любых законах распределения случайных
величин в выборках
97. При решении задачи о расхождении или совпадении двух выборок имеет
ли значение вопрос о независимости друг от друга сравниваемых выборок?
a) Ответ будет одинаковым как в случае зависимых, так и в случае независимых друг
от друга выборок
b) Ответ будет различным в зависимости от того, какие выборки сравниваются –
зависимые друг от друга или независимые
c) Выборки случайных величин всегда являются независимыми друг от друга
98. Оценивалось время действия препарата на одной и той же группе
пациентов. Можно ли считать полученные два статистических ряда
независимыми выборками?
a) Да
b) Нет
c) Можно, если оформить выборки в виде интервальных вариационных рядов
99. Измерялась температура тела самок и самцов тушканчика. Можно ли
считать полученные два статистических ряда независимыми выборками?
a) Да
b) Нет
c) Можно, если оформить выборки в виде интервальных вариационных рядов
100. Вероятность различия средних арифметических двух выборок (при
условии соответствия эмпирических распределений нормальному)
определяется с помощью таблиц:
a) Критериев Стьюдента
b) Критериев Фишера
c) Критериев согласия Х2
d) Других таблиц
101. Вероятность различия дисперсий двух выборок (при условии
соответствия эмпирических распределений нормальному) определяется с
помощью таблиц:
a) Критериев Стьюдента
b) Критериев Фишера
c) Критериев согласия Х2
d) Других таблиц
102. Критерии Стьюдента и Фишера являются:
a) Параметрическими
b) Непараметрическими
c) Критериями согласия Х2
d) Другими критериями
103. При решении задачи о различии двух выборок какая гипотеза
проверяется?
a) Расхождение выборок не случайно
b) Расхождение выборок случайно
c) Эмпирические частоты в выборках не совпадают
d) Эмпирические частоты в выборках совпадают
104. При решении задачи о различии двух выборок обычно задаются уровнем
значимости. В чём смысл этого понятия?
a) Это вероятность того, что принятая гипотеза о случайном характере различия
выборок подтверждается
b) Это вероятность того, что принятая гипотеза не подтверждается
c) Это вероятность того, что эмпирические частоты в выборках не совпадают
d) Это вероятность того, что эмпирические частоты в выборках совпадают
105. Что понимается под корреляцией?
a) Это зависимость между неслучайными величинами
b) Это зависимость между случайными величинами
c) Это функциональная зависимость
106. Существует ли и какого типа корреляция между ростом человека и его
весом?
a) Существует; отрицательная
b) Существует; положительная
c) Не существует
107. Корреляция между двумя случайными величинами является
положительной, если:
a) С возрастанием одной величины другая уменьшается
b) С возрастанием одной величины другая тоже возрастает
c) С возрастанием одной величины другая не меняется
108. Корреляция между двумя случайными величинами является
отрицательной, если:
a) С возрастанием одной величины другая уменьшается
b) С возрастанием одной величины другая тоже возрастает
c) С возрастанием одной величины другая не меняется
109. Корреляция между двумя случайными величинами отсутствует, если:
a) С возрастанием одной величины другая уменьшается
b) С возрастанием одной величины другая тоже возрастает
c) С изменением одной величины нельзя заметить тенденцию изменения другой
110. Корреляция между двумя случайными величинами является линейной,
если:
a) Зависимость между ними может быть аппроксимирована функцией вида Y=A ± BX
(Х – переменная, А и В константы)
b) Зависимость между ними может быть аппроксимирована любой другой функцией
c) Величины имеют одинаковую размерность
111. Корреляция между двумя случайными величинами является нелинейной,
если:
a) Зависимость между ними может быть аппроксимирована функцией вида Y=A ± BX
(Х – переменная, А и В константы)
b) Зависимость между ними может быть аппроксимирована любой другой функцией
c) Величины имеют одинаковую размерность
112. Качественно наличие корреляции устанавливается путём:
a) Построения гистограммы
b) Построения корреляционного поля
c) Построения полигона распределений
113. Корреляционным полем называется:
a) Диаграмма зависимости одной случайной величины от другой в виде точечного
графика
b) Гистограмма распределений одной величины при изменении другой
c) Полигон распределений значений величин в выборках
114. По степени корреляции (силе связи) корреляция может быть:
a) Пропорциональная, непропорциональная, обратно пропорциональная
b) Сильная, средняя, слабая
c) Неявная, явная, очевидная
115. Для определения степени корреляции (силы связи)необходимо
вычислить:
a) Доверительные интервалы в сравниваемых выборках
b) Выборочные характеристики сравниваемых выборок
c) Коэффициент корреляции
116. Какое соответствие между значением коэффициента корреляции r и степенью корреляции (силой связи) является правильным?
a)  - cильная корреляция,
- cильная корреляция,  – средняя корреляция,
– средняя корреляция,
 –слабая корреляция
–слабая корреляция
b) Значение коэффициента корреляции не определяет степень корреляции (силу связи)
c) r > 1 - cильная корреляция, r < -1 – средняя корреляция, r = 0 слабая корреляция
117. На диаграмме изображено корреляционное поле. Что можно сказать о
корреляции между Y и Х?
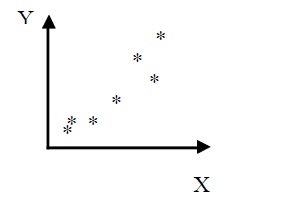
a) Корреляция отсутствует
b) Корреляция есть, положительная, линейная
c) Корреляция есть, отрицательная, линейная
d) Корреляция есть, отрицательная, нелинейная
e) Корреляция есть, положительная, нелинейная
118. На диаграмме изображено корреляционное поле. Что можно сказать о
корреляции между Y и Х?

a) Корреляция отсутствует
b) Корреляция есть, положительная, линейная
c) Корреляция есть, отрицательная, линейная
d) Корреляция есть, отрицательная, нелинейная
e) Корреляция есть, положительная, нелинейная
119. На диаграмме изображено корреляционное поле. Что можно сказать о
корреляции между Y и Х?

a) Корреляция отсутствует
b) Корреляция есть, положительная, линейная
c) Корреляция есть, отрицательная, линейная
d) Корреляция есть, отрицательная, нелинейная
e) Корреляция есть, положительная, нелинейная
120. На диаграмме изображено корреляционное поле. Что можно сказать о
корреляции между Y и Х?
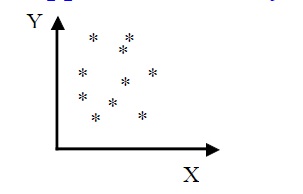
a) Корреляция отсутствует
b) Корреляция есть, положительная, линейная
c) Корреляция есть, отрицательная, линейная
d) Корреляция есть, отрицательная, нелинейная
e) Корреляция есть, положительная, нелинейная
121. На диаграмме изображено корреляционное поле. Что можно сказать о
корреляции между Y и Х?

a) Корреляция отсутствует
b) Корреляция есть, положительная, линейная
c) Корреляция есть, отрицательная, линейная
d) Корреляция есть, отрицательная, нелинейная
e) Корреляция есть, положительная, нелинейная
122. При корреляционном анализе данных на компьютере часто результаты
получают в виде корреляционной матрицы. Что она собой представляет?
a) Это гистограмма распределения вариант в выборках
b) Это двумерная таблица, в которой приведены все выборочные характеристики по
всему массиву данных
c) Это двумерная таблица, в которой приведены коэффициенты корреляции для всех
парных сочетаний величин из массива экспериментальных данных
d) Это таблица, содержащая значения коэффициента корреляции только для двух
величин из массива экспериментальных данных
123. Какое из утверждений является правильным?
a) Коэффициент корреляции может быть вычислен для любых законов распределения
случайных величин и для всех видов корреляции
b) Коэффициент корреляции может быть вычислен только при нормальном законе
распределения и линейной корреляции
c) Коэффициент корреляции может быть вычислен при любых законах распределения
случайных величин, но только для линейных корреляций
124. Значение коэффициента корреляции может изменяться в пределах
a) От 0 до +1
b) От -1 до + 1
c) От -  до +
до + 
125. Если значение коэффициента корреляции равно ± 1, то:
a) Корреляционная зависимость между случайными величинами может считаться
функциональной зависимостью
b) Корреляционная зависимость является слабо выраженной
c) Корреляционная зависимость отсутствует
126. Задачей регрессионного анализа является:
a) Подтверждение наличия корреляционной связи между случайными величинами
b) Нахождение уравнения, описывающего корреляцию
c) Разбиение статистического ряда на классовые интервалы
127. Проводить регрессионный анализ имеет смысл, если:
a) Корреляция слабая или отсутствует
b) Корреляция сильная или хотя бы средняя
c) Регрессионный анализ имеет смысл проводить всегда
128. Если корреляция между двумя случайными величинами линейная и
отрицательная, то уравнение регрессии имеет вид:
a) Y = A + B * X (А и В – числовые константы, а Х и Y - переменные)
b) Y = A - B * X (А и В – числовые константы, а Х и Y - переменные)
c) Y = A - B * X^2 (А и В – числовые константы, а Х и Y - переменные)
129. Если корреляция между двумя случайными величинами линейная и
положительная, то уравнение регрессии имеет вид:
a) Y = A + B * X (А и В – числовые константы, а Х и Y - переменные)
b) Y = A - B * X (А и В – числовые константы, а Х и Y - переменные)
c) Y = A - B * X^2 (А и В – числовые константы, а Х и Y - переменные)
130. Уравнение регрессии имеет вид: Y = A + B ⋅ X (А и В – числовые
константы, Х – независимая переменная). Какой смысл имеет Y?
a) Y – среднее арифметическое всей выборки зависимых переменных
b) Y – среднее групповое значение зависимой переменной
c) Y – любое значение зависимой переменной
131. Уравнение множественной линейной регрессии имеет вид:
a)  (Аi и Вi – константы, а Хi и Y -переменные)
(Аi и Вi – константы, а Хi и Y -переменные)
b)  (Аi и Вi – числовые константы, а Хi и Y
(Аi и Вi – числовые константы, а Хi и Y
c) Y может зависеть только от одного значения Х
132. Уравнение регрессии позволяет:
a) Построить гистограмму распределения зависимой переменной
b) Прогнозировать изменчивость одного признака при изменении других
c) Снизить значение стандартной ошибки выборочного среднего
133. При регрессионном анализе данных на компьютере какой параметр в
списке выходных данных свидетельствует об удовлетворительной
аппроксимации эмпирических данных подобранным регрессионным
уравнением?
a) Критерий согласия X^2
b) Коэффициент детерминации R^2
c) Критерий Фишера
d) Критерий Стьюдента
134. При регрессионном анализе данных на компьютере в списке выходных
данных выводится значение коэффициента детерминации R^2. При каком значении R^2 аппроксимация эмпирических данных подобранным уравнением регрессии может считаться удовлетворительной?
a) Если R^2> 1
b) Если 0,8 < R^2< 0,95
c) Если R^2> критерия Фишера
d) Если R^2> критерия Стьюдента
135. При регрессионном анализе данных на компьютере в списке выходных
данных выводится значение коэффициента детерминации R^2. При каком значении R^2 можно говорить о высокой точности аппроксимации эмпирических данных подобранным уравнением регрессии?
a) Если R^2 > 0,95
b) Если 0,8 < R^2< 0,95
c) Если R^2> критерия Фишера
d) Если R^2> критерия Стьюдента
136. При регрессионном анализе данных на компьютере в списке выходных
данных выводится значение коэффициента Р («Р – значение»). При каком значении Р можно говорить о незначимости какого – либо коэффициента регрессии в найденном уравнении?
a) Если P > коэффициента детерминации R^2
b) Если Р < 0,05
c) Если P > 0,05
137. При регрессионном анализе данных на компьютере, какой параметр в
списке выходных данных свидетельствует о значимости того или иного
коэффициента регрессии в найденном уравнении регрессии?
a) Критерий согласия X^2
b) Коэффициент детерминации R^2
c) Критерий Фишера
d) Критерий Стьюдента
e) «Р – значение»
138. На диаграмме изображено корреляционное поле с проведённой линией
регрессии. Какого типа уравнением описывается эта линия?
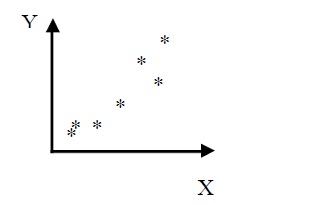
a) Y = A + B * X (А и В – константы)
b) Y = A - B * X (А и В – константы)
c) Y = A - B * X^2 (А и В – константы)
d) Y = A + B * X^2 (А и В – константы)
139. На диаграмме изображено корреляционное поле. Что можно сказать о
корреляции между Y и Х?

a) Y = A + B * X (А и В – константы)
b) Y = A - B * X (А и В – константы)
c) Y = A - B * X^2 (А и В – константы)
d) Y = A + B * X^2 (А и В – константы)
140. Непараметрические методы статистического анализа могут быть
применены, если известно, что:
a) эмпирическое распределение соответствует Нормальному закону распределения;
b) эмпирическое распределение соответствует Биномиальному закону распределения;
c) эмпирическое распределение соответствует распределению Пуассона;
d) априорного знания закона распределения при использовании непараметрических
методов не требуется.
141. Непараметрические методы статистического анализа могут быть
применены, только если:
a) величины в выборке выражены в интервальной шкале;
b) величины в выборке выражены в номинальной шкале;
c) тип шкалы не имеет значения;
d) величины в выборке выражены в относительной шкале;
142. Непараметрические методы статистического анализа могут быть
применены, если:
a) величины в выборке являются только численными;
b) величины в выборке являются только качественными;
c) тип величин не имеет значения;
d) величины в выборке выражены только целочисленными значениями;
143. Непараметрические методы статистического анализа не могут быть
применены, если априорно не известно, что:
a) эмпирическое распределение соответствует Нормальному закону распределения;
b) эмпирическое распределение соответствует Биномиальному закону распределения;
c) эмпирическое распределение соответствует распределению Пуассона;
d) априорного знания закона распределения при использовании непараметрических
методов не требуется.
144. Непараметрические методы статистического анализа не могут быть
применены, если:
a) предварительно не вычислены все выборочные характеристики;
b) предварительно не вычислена только выборочная дисперсия;
c) предварительное вычисление выборочных характеристик при использовании
непараметрических методов не требуется.
d) не известно математическое ожидание данного статического ряда;
145. При решении многих задач статистического анализа вычисляется
уровень значимости, который означает:
a) вероятность ошибки, если нулевую гипотезу принять;
b) вероятность ошибки, если нулевую гипотезу отбросить;
c) доверительную вероятность;
d) мощность используемого статистического критерия.
146. Решение задачи о достоверности различия двух независимых выборок
возможно на основе вычисления непараметрических критериев:
a) критерия Спирмена;
b) критерия Манна – Уитни;
c) критерия Вилкоксона;
d) критерия корреляции Пирсона.
147. Методом вычисления критерия Манна – Уитни возможно решение
следующей задачи:
a) выявление корреляционной зависимости между двумя зависимыми выборками;
b) выявление корреляционной зависимости между двумя независимыми выборками;
c) определение значимости различия двух независимых выборок;
d) определение значимости различия нескольких независимых выборок.
148. Методом вычисления критерия Манна – Уитни возможно решение
следующей задачи:
a) вычисление выборочных характеристик;
b) установление и описание корреляции между двумя зависимыми выборками;
c) установление значимости различия двух зависимых выборок;
d) установление значимости различия двух независимых выборок.
149. При решении задачи методом вычисления критерия Манна – Уитни
проверяется следующая нулевая гипотеза (Н0):
a) расхождение двух независимых выборок является случайным;
b) две выборки являются зависимыми;
c) расхождение двух независимых выборок является неслучайным;
d) расхождение нескольких независимых выборок является случайным;
150. Решение задачи о достоверности различия двух зависимых выборок
возможно на основе вычисления непараметрических критериев:
a) критерия Спирмена;
b) критерия Манна – Уитни;
c) критерия Вилкоксона;
d) критерия корреляции Пирсона.
151. Методом вычисления критерия Вилкоксона возможно решение
следующей задачи:
a) выявление корреляционной зависимости между двумя зависимыми выборками;
b) выявление корреляционной зависимости между двумя независимыми выборками;
c) определение значимости различия двух зависимых выборок;
d) определение значимости различия нескольких зависимых выборок.
152. Методом вычисления критерия Вилкоксона возможно решение
следующей задачи:
a) вычисление выборочных характеристик;
b) установление и описание корреляции между двумя зависимыми выборками;
c) установление значимости различия двух зависимых выборок;
d) установление значимости различия двух независимых выборок.
153. При решении задачи методом вычисления критерия Вилкоксона
проверяется следующая нулевая гипотеза (Н0):
a) две зависимые выборки принадлежат одной статистической совокупности;
b) две выборки являются зависимыми;
c) расхождение двух независимых выборок является неслучайным;
d) расхождение нескольких независимых выборок является случайным;
154. Одним из условий применимости критерия Вилкоксона является:
a) Сравниваемые две выборки должны быть независимыми;
b) Сравниваемые две выборки должны быть попарно связанными;
c) Количество сравниваемых выборок должно быть не менее трёх;
d) Между сравниваемыми двумя выборками должна отсутствовать корреляционная
зависимость.
155. При решении задачи методом вычисления критерия Вилкоксона должно
выполняться условие:
a) объёмы выборок должн






