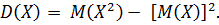Математическое ожидание характеризует положение случайной величины на числовой оси, определяя некоторое среднее значение, около которого сосредоточены все возможные значения случайной величины.
Для непрерывных случайных величин с плотностью распределения f(x) математическое ожидание равно определённому интегралу: 
Пример 4.2.
Найти математическое ожидание дискретной случайной величины Х, зная закон её распределения.
| Х | -1 | ||||
| р | 0,05 | 0,2 | 0,4 | 0,3 | 0,05 |
По формуле 
находим:
Пример 4.3.
Найти математическое ожидание непрерывной случайной величины Х, зная закон её распределения.
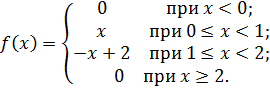
По формуле 
находим:
Свойства математического ожидания:
1. Математическое ожидание постоянной величины равно этой постоянной: 
.
2. Постоянный множитель можно выносить за знак математического ожидания: 
3. Математическое ожидание алгебраической суммы случайных величин равно алгебраической сумме их математических ожиданий: 
4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: 
5. Математическое ожидание отклонения случайной величины от её математического ожидания всегда равно нулю: 
Дисперсия характеризует рассеяние (отклонение) случайной величины относительно математического ожидания.
.
Для дисперсии случайной величины: 
Для непрерывных случайных величин с плотностью вероятности f(x): 
Размерность дисперсии равна квадрату случайной величины и её неудобно использовать для характеристики разброса, поэтому удобнее применять корень квадратный из дисперсии - среднее квадратическое отклонение. Эта величина даёт представление о размахе колебаний случайной величины около математического ожидания.
.
Пример 4.4.
Случайная величина задана следующим рядом распределений.
| Х | -1 | |||
| р | 0,1 | 0,3 | 0,4 | 0,2 |
Найти математическое ожидание и дисперсию этой величины.
Для нахождения математического ожидания воспользуемся формулой , а для дисперсии - Результаты вычисления сведём в таблицу.
| x | pi | xipi | xi - M(X) | (xi - M(X))2 | (xi - M(X))2 pi |
| -1 | 0,1 0,3 0,4 0,2 | -0,1 0,4 0,4 | -1,7 -0,7 0,3 1,3 | 2,89 0,49 0,09 1,69 | 0,289 0,147 0,036 0,338 |
| 0,7 | 0,81 |
Из таблицы следует, что М(Х)=0,7; D(X)=0,81.
Пример 4.5.
Случайная величина задана плотностью вероятности:
Найти математическое ожидание и дисперсию этой величины.
По формуле находим:
Далее по формуле 
Основные свойства дисперсии:
1. Дисперсия алгебраической суммы двух независимых случайных величин равна сумме дисперсий этих величин: D(X±Y)= D(X) ± D(Y).
2. Дисперсия постоянной величины С равна нулю: D(C) = 0.
3. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СX)= С2 D(X).
4. Дисперсия случайной величины Х равна разности между математическим ожиданием квадрата случайной величины и квадратом её математического ожидания: 
