Основы теории вероятностей

Раздел 2. Основные понятия дискретной математики. Основы теории вероятностей

1. Элементы математической логики.

2. Основные понятия комбинаторики.

3. Основы теории вероятности.

4. Случайные величины.

5. Нормальный закон распределения. Закон больших чисел.

Элементы математической логики

Математическая логика – это раздел математики, который занимается исследованием высказываний с точки зрения их формального строения.

Опр. Высказывание – это повествовательное предложение, о котором можно однозначно сказать истинно оно или ложно.

Пример 1.1. Высказывания:

1. Москва - столица России. (и)

2. К форменным элементам крови относятся эритроциты, лейкоциты, тромбоциты. (и)

3. Айсберги чаще всего встречаются на экваторе. (л)

4. У здорового человека температура тела 26,6°С. (л)

Опр. Отрицанием высказывания А называется новое высказывание, которое обозначается (читается «не А») и истинно, если А ложно, и ложно, если А истинно.

А

Опр. Дизъюнкцией высказываний А и В называется новое высказывание, которое обозначается (читается «А или В») и ложно только в том случае, если ложны оба высказывания, а в остальных случаях истинно.

А	В	А ∪ В

Опр. Конъюнкцией высказываний А и В называется новое высказывание, которое обозначается (читается «А и В») и истинно только в том случае, когда истинны оба высказывания, а в остальных случаях - ложно.

А	В	А ∩ В

Основные понятия комбинаторики

Комбинаторика – раздел математики, в котором изучаются задачи выбора элементов из заданного множества и размещения этих элементов в каком-либо порядке.

Опр. Группы составленные из каких – либо элементов называется соединениями.

Опр. Размещением из n-элементов по m в каждом (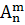) называются такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их расположения. Количество размещений вычисляется по формуле:

Пример 2.1.

Сколькими способами из 8 кандидатур можно выбрать 5 медсестёр в 5 отделений?

Ответ: 6720 размещений.

Опр. Перестановкой из n-элементов называются такие соединения из всех элементов, которые отличаются друг от друга порядком расположения. Количество перестановок вычисляется по формуле:

Пример 2.2.

Найти число вариантов различных списков из 7 пациентов.(Списки считаются разными, если они отличаются порядком расположения элементов.)

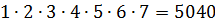
Ответ: 5040 списков.

Опр. Сочетанием из n-элементов по m в каждом () называются такие соединения, которые отличаются друг от друга хотя бы одним элементом. Количество сочетаний вычисляется по формуле.

Пример 2.3.

В клетке содержится 10 мышей. Необходимо отобрать 4 мыши для проведения эксперимента. Сколькими способами это можно сделать?

Ответ: 210 способов.

Основы теории вероятностей

Теория вероятностей – это раздел математики изучающий закономерности массовых случайных событий.

Изучение каждого явления в порядке наблюдения или производства опыта связанно с осуществлением некоторого комплекса условий (испытаний). Всякий результат или исход испытания называется событием.

Опр. Если событие при заданных условиях может произойти или не произойти, то оно называется случайным.

Опр. В том случае, когда событие непременно должно произойти, то оно называется достоверным, а в том случае, когда оно заведомо не может произойти – невозможным.

Опр. События называются несовместными, если каждый раз возможно появление только одного из них.

Опр. События называются совместными, если в данных условиях появление одного из этих событий не исключает появления другого при том же испытании.

Опр. События называются противоположными, если в условиях испытания они, являясь единственными его исходами, несовместны.

Вероятность события рассматривается как мера объективной возможности появления случайного события.

Классическое определение вероятности:

Вероятностью события А называется отношение числа исходов m, благоприятствующих наступлению данного события А, к числу n всех исходов (несовместных, единственно возможных и равновозможных), т. е.

Вероятность любого события не может быть меньше нуля и больше 1, т. е.

Невозможному событию соответствует вероятность а достоверному – вероятность

Пример 3.1.

В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?

Общее число различных исходов есть n = 1000. Число исходов, благоприятствующих получению выигрыша, составляет m = 200. Согласно формуле
P 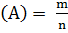, получим:

Ответ: вероятность выигрыша 0,2 или 20%.

Теорема сложения вероятностей несовместных событий: Вероятность одного из нескольких попарно несовместных событий, безразлично какого равна сумме вероятностей этих событий:

Теорема сложения вероятностей совместных событий:

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Событие, противоположное событию А (т.е. ненаступление события А), обозначают через

Сумма вероятностей двух противоположных событий равна 1. = 1

Теорема умножения вероятностей независимых событий:

Вероятность совместного появления (или произведения) двух независимых событий равна произведению вероятностей этих событий:

Теорема умножения вероятностей зависимых событий:

Вероятность совместного появления (или произведения) двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие осуществилось.

Пример 3.2.

В группе из 20 студентов 5 студентов не подготовили задание. Какова вероятность того, что два первых студента, вызванные наугад, будут не готовы к ответу.

Вероятность того, что 1 студент не готов к ответу, вероятность того, что и 2 студент также не готов, как и первый,

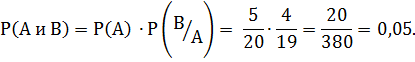
Ответ: вероятность того, что два первых студента, вызванные наугад, будут не готовы к ответу – 5%.

Случайные величины

Опр. Случайной называют величину, которая принимает в результате испытания то или иное возможное значение, заранее неизвестное, меняющееся от испытания к испытанию и зависящее от случайных обстоятельств.

Дискретной называют такую случайную величину, которая принимает счётное множество значений, т.е. такое множество, элементы которого можно посчитать.

Непрерывной называют такую случайную величину, которая может принимать любые значения в определённом интервале.

Случайная величина считается заданной, если известен закон распределения случайной величины.

Опр. Распределением (законом распределения)случайной величины называется всякое соотношение между возможными значениями случайной величины и соответствующими им вероятностями.

Значение случайной величины х_i	x₁	x₂	……	x_n
Вероятность значений p_i	p₁	p₂	…….	p_n

Табличную форму задания называют также рядом распределения.

Пример 4.1.

Построить график ряда распределения значений частоты пульса в гипотетической группе из 47 человек.

Значение случайной величины уд/мин
Значения вероятности p (х_i)

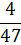
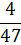
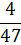
По данным таблицы построен график, который называется многоугольником распределения вероятностей.

Опр. Функция распределения определяет вероятность того, что случайная величина Х принимает значение, меньшее фиксированного действительного числа х, т.е.

Свойства функции распределения:

1. Функция распределения случайной величины есть неотрицательная функция, заключённая между нулём и единицей: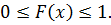

2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси, и для любых выполняется равенство:

3. На минус бесконечности функция распределения равна нулю, на плюс бесконечности – единице, т.е.

Опр. Функцию f(x) называют дифференциальной функцией распределения, или плотностью распределения (плотностью вероятности),непрерывной случайной величины Х.

Основные свойства функции распределения:

1. Для любых х дифференциальная функция распределения неотрицательна, т.е.

2. Для дифференциальной функции распределения имеет место равенство: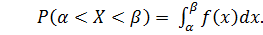

3. Для дифференциальной функции распределения имеет место равенство: Это свойство называется условием нормировки плотности вероятностей.