Стационарная теплопроводность через плоскую стенку

1. Однородная плоская стенка (рис. 9.2).Температура поверхностей стенки t_{ст 1} и t_{ст 2}.Плотность теплового потока: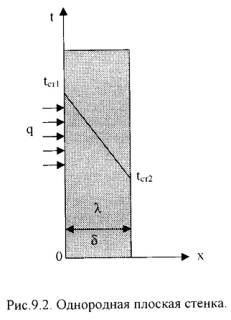

q=-λ∙∂t/∂n=-λ∙∂t/∂x=-λ ∙(t_{cт 2}- t_{cт 1})/(x_{cт 2}- x_{cт 1})

Или

q = λ ∙Δ t /Δ x. (9.13)

Так как Δ x=δ, то

q= (λ/δ)∙Δ t. (9.14)

R=δ/λ - термическое сопротивление теплопроводности стенки [(м²∙К)/Вт]. Поэтому плотность теплового потока:

q =(t_{ст 1}– t_{ст 2})/ R. (9.15)

Общее количество теплоты, проходя-щее через поверхность F за время τ:

Q=q∙F∙τ =(t_{ст 1}– t_{ст 2})/ R·F∙τ. (9.16)

Температура тела в точке с координатой х:

t_x=t_{ст 1}–(t_{ст 1}– t_{ст 2})∙ x/δ. (9.17)

2. Многослойная плоская стенка. Рассмотрим трёхслойную стенку (рис. 9.3). Температура наружных поверхностей стенок t_{ст 1} и t_{ст 2}; коэффициенты теплопроводности слоев λ ₁, λ ₂, λ ₃; толщина слоев δ ₁, δ ₂, δ ₃.

Плотности тепловых потоков через каждый слой стенки: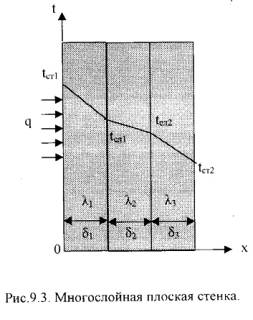

q=λ ₁/ δ ₁∙(t_{ст 1}- t_{сл 1}), (9.18)
q=λ ₂/ δ ₂∙(t_{сл 1}– t_{сл 2}), (9.19)
q=λ ₃/ δ ₃∙(t_{сл 2}– t_{ст 2}), (9.20)

Разрешая (9.18)-(9.20) относитель-но разности температур и складывая, получим:

q = (t_{ст 1}- t_{ст 2})/ R _o, (9.21)

где R _o=(δ ₁/ λ ₁+ δ ₂/ λ ₂+ δ ₃/ λ ₃) - общее термическое сопротивление теплопроводности трёхслойной стенки.

Температура слоев определяется по формулам:

t_{сл 1}= t_{ст 1}- q ∙(δ ₁/ λ ₁). (9.22)
t_{сл 2}= t_{сл 1}– q· (δ ₂/ λ ₂). (9.23)

Стационарная теплопроводность через цилиндрическую стенку

1. Однородная цилиндрическая стенка. Рассмотрим однородный цилиндр длиной l, внутренним диаметром d ₁и внешним диаметром d ₂ (рис. 9.4). Температуры поверхностей стенки t_{ст 1} и t_{ст 2}. Уравнение теплопроводности по закону Фурье в цилиндрических координатах: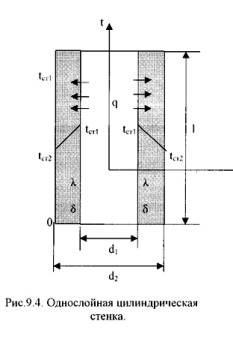

Q = -λ∙2∙ π∙r·l·∂t/∂r (9.24)

Или, в интегральной форме,

Q = 2· π·λ·l ·Δ t/ln (d ₂/ d ₁), (9.25)

где Δ t = t_{ст 1}– t_{ст 2} - температурный напор; λ - κоэффициент теплопроводности стенки.

Введём понятие теплового потока единицы длины цилиндрической поверхности (линейная плотность теплового потока):

q_l=Q/l =2· π·λ ·Δ t/ln (d ₂/ d ₁), [Вт/м]. (9.26)

Температура тела внутри стенки в точке с координатой d_х:

t_x=t_{ст 1}–(t_{ст 1}– t_{ст 2})· ln (d _x/ d ₁)/ ln (d ₂/ d ₁). (9.27)

2. Многослойная цилиндрическая стенка. Допустим, цилиндрическая стенка состоит из трех плотно прилегающих слоев (рис. 9.5). Температура внутренней поверхности стенки t_{ст 1}, наружной t_{ст 2}, коэффициенты теплопроводности слоев λ ₁, λ ₂, λ ₃, диаметры поверхностей слоев d ₁, d ₂, d ₃, d ₄.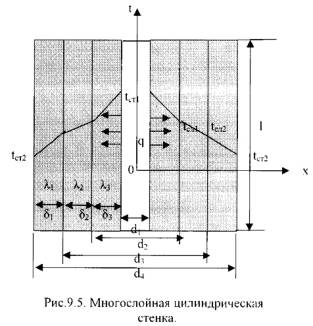

Тепловые потоки в слоях:
1-й слой

Q= 2 ·π·λ ₁· l ·(t_{ст 1}– t_{сл 1})/ln(d ₂/ d ₁), (9.28)
2-й слой

Q =2· π·λ ₂· l ·(t_{сл 1}– t_{сл 2})/ln(d ₃/ d ₂), (9.29)
3-й слой

Q =2· π·λ ₃· l ·(t_{сл 2}– t_{ст 2})/ln(d ₄/ d ₃). (9.30)

Решая совместно уравнения (9.28)-(9.30), получим для потока через трёхслойную стенку:

Q =2· π·l ·(t_{ст 1}– t_{ст 2})/[ln(d ₂/ d ₁)/ λ ₁+ln(d ₃/ d ₂)/ λ ₂+ln(d ₄/ d ₃)/ λ ₃]. (9.31)

Для линейной плотности теплового потока:

q_l=Q/l =2· π ·(t_{ст 1}– t_{ст 2})/[ln(d ₂/ d ₁)/λ₁+ln(d ₃/ d ₂)/ λ ₂+ln(d ₄/ d ₃)/ λ ₃]. (9.32)

Температуру между слоями находим из уравнений:

t_{сл 1}= t_{ст 1}– q_l ·ln(d ₂/ d ₁)/2· π·λ ₁. (9.33)
t_{сл 2}= t_{сл 1}– q_l ·ln(d ₃/ d ₂)/2· π·λ ₂ . (9.34)

9.4. Стационарная теплопроводность через шаровую стенку

Пусть имеется полый шар (рис. 9.6), внутренним диаметром d ₁ и внешним диаметром d ₂. Температура внутренней поверхности стенки t_{ст 1}, температура наружной поверхности стенки t_{ст 2}, коэффициент теплопроводности стенки λ. Уравнение теплопроводности по закону Фурье в сферических координатах:

Q = - λ ·4· π·r ²· ∂t/∂r (9.35)