ЗАВДАННЯ 1.
Пiдзавдання 1_1. Визначити iндивiдуальний номер варіанту.
Етап 1. Перевести номер залікової книжки до двійкової системи.
Наприклад, якщо номер залікової книжки у десятковій системі числення дорівнює 14101, то еквівалентним двійковим числом буде (11011100010101)2.
Етап 2.Поставити у відповідність двійковій формі запису номеру заліко-вої книжки слово виду b12b11b10b9b8b7b6b5b4b3b2b1b0 (за необхідності, зайві роз-ряди ліворуч відкинути). Для розглянутого прикладу: b12 = 1; b11 = 0; b10 = 1; b9 = 1; b8 = 1; b7 = 0; b6 = 0; b5 = 0; b4 = 1; b3 = 0; b2 = 1; b1 = 0; b0 = 1.
Етап 3. Занести отримані значення bi (і = 0, 1,..., 12) до табличної форми.
Для розглянутого прикладу, таблиця значень набуде наступного вигляду:
| b 12 | b 11 | b 10 | b 9 | b 8 | b 7 | b 6 | b 5 | b 4 | b 3 | b 2 | b 1 | b 0 |
Етап 4. Занести до наведеної нижче шаблонної таблиці істинності пере-микальних функцій f1 і f2 конкретні значення множини { bi } (і = 0, 1,..., 12).
| x1 | x2 | x3 | x4 | f1 | f2 |
| b0 | |||||
| b1 | 0 | ||||
| b2 | |||||
| b3 | |||||
| b5 | b4 | ||||
| b7 | b6 | ||||
| b8 | |||||
| b9 | |||||
| b10 | |||||
| b12 | |||||
| b11 |
Для розглянутого прикладу, отримаємо наступну конкретизовану таблицю:
| x1 | x2 | x3 | x4 | f1 | f2 |
| b12 | |||||
Пiдзавдання 1_2. Знайти для сформованих вище (таблично заданих) перемикальних функцій f1 і f2 досконалу диз'юнктивну нормальну форму (ДДНФ) і досконалу кон'юнктивну нормальну форму (ДКНФ), побудувати відповідні комбінаційні схеми.
Пiдзавдання 1_3. Спростити досконалі диз'юнктивні нормальні форми (ДДНФ) перемикальних функцій f1 і f2, застосовуючи до них правила склею-вання та поглинання, закони та тотожності алгебри логіки; побудувати комбіна-ційні схеми для спрощених виразів ДДНФ перемикальних функцій f1 і f2.
ЗАВДАННЯ 2.
Пiдзавдання 2_1. Визначити iндивiдуальний номер варіанту: спираючися на результати виконання підзавдання 1.1, сформувати двійкове слово виду b3b2b1b0; вибрати з наведеної нижче таблиці відповідну перемикальну функцію.
Наприклад, для розглянутого у завданні 1 випадку, b3b2b1b0 дорівнюватиме 0101, що відповідає шостій за переліком перемикальній функції наведеної нижче таблиці.



Пiдзавдання 2_2. Застосувати до вибраної перемикальної функції наступні дії: спростити, використовуючи закони та тотожності алгебри логіки; обчислити таблицю істинності спрощеного логічного виразу; побудувати відповідну комбінаційну схему.
ЗАВДАННЯ 3. Подати аналiтичнi вирази перемикальних функцій f1 і f2, отриманi у пiдсумку виконання завдання 1, у базисах Пiрса та Шефера, побудувати для кожного з них відповідні комбінаційні схеми.
ЗАВДАННЯ 4.
Пiдзавдання 4.1. Визначити, чи є одна з наведених нижче перемикальних функцій лінійною.
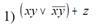
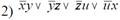
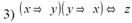

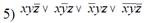
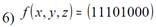

Пiдзавдання 4.2. Визначити, чи є одна з наведених нижче перемикальних функцій монотонною.
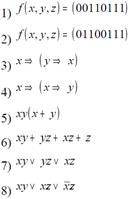

Пiдзавдання 4.3. Визначити, чи є одна з наведених нижче перемикальних функцій самоподвiйною.
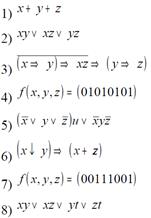
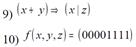
Пiдзавдання 4.4. Визначити, чи є одна з наведених нижче систем перемикальних функцій функціонально повною.
Додаток А






