ЛАБОРАТОРНА РОБОТА 3
Тема: Основні положення та означення комп`ютерної логіки. Частина 3. Початкові поняття про побудову комбінаційних схем для перемикальних функцій, заданих таблично й аналітично; повнота систем перемикальних функцій.
Мета роботи: опановування базових методів отримання комбінаційних схем на основі табличного й аналітичного подання перемикальних функцій, методiв визначення функціонально повних систем перемикальних функцiй.
Базові поняття:
- елементарні перемикальні функції; логічні елементи; комбінаційна схема; цифровий автомат; побудова комбінаційних схем, які реаліують перемикальні функції, задані аналітичними виразами; побудова комбінаційних схем, які реаліують перемикальні функції, задані таблицями істинності;
- функцiонально повнi системи перемикальних функцiй; теорема про подання перемикальних функцiй через диз`юнкцiю, кон`юнкцiю та заперечення; теорема про функцiональну повноту деяких поширених систем перемикальних функцiй; перемикальнi функцiї, що зберiгають константу 0 (клас P0) i константу 1 (клас P1), самоподвiйнi (клас S), монотоннi (клас M) i лiнiйнi (клас L) перемикальнi функцiї; власнi та замкненi класи перемикальних функцiй (класи Поста); теорема про власність i замкненiсть класiв P0, P1, S, M, i L; теорема Поста про функiональну повноту й її наслiдки.
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ
Початкові поняття про побудову комбінаційних схем для перемикальних функцій, заданих таблично й аналітично
Поняття перемикальної функції
Для формального опису вузлів комп'ютерів у процесі їх синтезу й аналізу, використовується математичний апарат алгебри логіки (булевої алгебри, алгебри Буля), що є одним із важливих розділів математичної логіки, основні положення якої розробив у ХІХ столітті англійський математик Джордж Буль.
Перемикальною функцією називають будь-яку функцію f(x1, x2,..., xn), залежну від n змінних (x1, x2,..., xn), для якої сама функція f і кожний із її аргументів xi (i = 1,..., n) приймають значення тільки з множини значень{0, 1}.
Перемикальну функцію (ПФ) також називають булевою функцією (БФ) або функцією алгебри логіки (ФАЛ).
Аргументи перемикальної функції називають двійковими (булевими) аргументами.
Сукупність двійкових змінних < x1, x2,..., xn >, яка являє собою комбінацію з нулів та одиниць, називають двійковим набором (або просто набором).
Якщо двійковий набір складається з n двійкових змінних, то можна отримати 2ⁿ різних двійкових наборів.
Кількість різних функцій алгебри логіки, що залежать від n змінних, дорівнює (2²)ⁿ.
Довільна перемикальна функція f може бути задана за допомогою наступних основних способів:
‒ табличним способом;
‒ у вигляді аналітичного виразу;
‒ вербально (у вигляді словесного формулювання);
‒ графічно.
Табличне подання перемикальної функції є вихідною формою в задачах синтезу цифрових схем і виконується у вигляді таблиці істинності.
Для задавання перемикальної функції n змінних у вигляді таблиці істинності, необхідно вказати її значення на кожному з її 2ⁿ можливих двійкових наборів.
Для компактного запису таблиці істинності, двійкові набори зручно представляти їхніми номерами.
Оскільки < x1, x2,..., xn > являє собою запис деякого цілого числа у двійковій системі числення, то номер набору визначається наступним чином: x1 2^(n-1) + x2 2^(n-2) +... + xn 2^ 0.
Перемикальна функція може бути задана шляхом перерахування номерів наборів, на яких вона приймає одиничне (або нульове) значення.
Приклад табличного способу задавання перемикальної функції від трьох змінних f(x1, x2, x3) наведено в таблиці 1.
Таблиця 1
| x1 | x2 | x3 | f |
Перемикальна функція для даного прикладу також може бути задана шляхом застосування компактного запису таблиці істинності, де двійкові набори представлено їх номерами, а саме: f(x1, x2, x3) = { 0, 3, 4, 6, 7 }.
Аналітичне задавання перемикальних функцій здійснюється за допомогою математичного запису формул у вигляді суперпозиції позначок елементарних логічних функцій алгебри логіки.
Приклад аналітичного подання перемикальної функції трьох змінних:
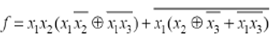
Як правило, аналітичне подання перемикальних функцій є проміжною формою в задачах синтезу та аналізу цифрових схем.
Графічне задавання перемикальних функцій здійснюється у виді схем із використанням умовних графічних позначень (УГП) логічних елементів.
Графічна форма подання перемикальних функцій є вихідною в задачах аналізу та кінцевою в задачах синтезу цифрових пристроїв.
Вербальне (словесне) задавання перемикальних функцій здійснюється у вигляді унаочнюючого й уточнюючого словесного опису.






