Введемо, з метою скорочення подальших записів, наступнi позначення:
– f = f (x1,…,xn) – довільна булева функція;
– fi – значення функції f на i-тому наборі значень змінних;
– Кi – констітуента одиницi, що відповідає зазначеному набору;
– Ri - констітуента нуля, що відповідає зазначеному набору;
– і= 
; x1Úx2Ú…Úxn= 
xі, x1*x2*…*xn= 
xi.
Для довільної булевої функції 
є справедливими наступні формули її розкладання по змінній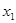 
:
; 
.
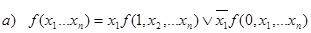Булевi функцiї 
і 
називають залишковими функціями для функції 
при її розкладаннi по змiннiй .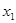
Аналогічно можна записати формули розкладання булевої функцiї по будь-якій її змінній.
Наприклад, розглянемо результат розкладання булевої функцiї за змінними 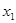і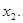 
:
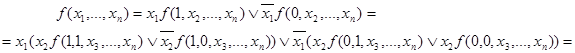
Узагальнюючи вище сказане, можна стверджувати, що для будь-якої булевої функцiї є справедливими наступні розкладання:
1) f (x1, …, xn) = 
fi Ki;
2) f (x1, …, xn) =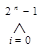 
(fi ÚRi).
Також є справедливим наступне твердження: якщо розкласти задану булеву функцiю за всіма змінними, то в результаті отримаємо ДДНФ (ДКНФ) даної булевої функцiї.
Дійсно, якщо розкласти задану булеву функцiю по всіх змінних, то в результаті отримаємо:
= fiKi = 
Kj.
Очевидно, що вираз у правій частині є ДДНФ.
Доведення для ДКНФ здiйснюється аналогічно.
Алгебра Жегалкіна
Алгеброю Жегалкіна називають множину булевих функцій, заданих у базисі Жегалкіна { Å, &, 1 }, який містить логічні операції додавання за модулем 2, кон’юнкції та встановлювання логічної одиниці.
Таблиці істинності елементарних булевих функцій додавання за модулем 2 і кон’юнкції зведено у таблиці 2.1.
У зазначеній таблиці представлено функцію f6 (із позначенням відповідної логічної операції Å) і функцію f1 (із позначенням відповідної логічної операції &).
Таблиця 2.1
| X | Y | f1 (х,у) | f6 (х,у) |
Основні тотожності (властивості) алгебри Жегалкіна:
1) комутативність:
H1 Å H2 = H2 Å H1
H1 & H2 = H2 & H1
2) асоціативність:
H1 Å (H2 Å H3) = (H1Å H2) Å H3
H1 & (H2 & H3) = (H1 & H2) & H3
3) дистрибутивність:
H1 & (H2 Å H3) = (H1 & H2) Å (H1 & H3)
4) властивості констант:
H & 1 = H
H & 0 = 0
H Å 0 = H
H Å H = 0
H & H = H
На основі операцій алгебри Жегалкіна можна представити всі інші булеві функції, наприклад:
/X = 1 + X
X v Y = X + Y + XY
X -> Y=1 + X + XY
X <-> Y = 1 + X + Y
Поліномом Жегалкіна (поліномом за модулем 2) від n змінних X1, X2,...,Xn називається вираз наступного вигляду:
C0 Å C1X1 Å C2X2 Å... Å CnXn Å C12X1X2 Å... Å C12...nX1X2...Xn,
де постійні величини Ck можуть приймати значення 0 або 1.
Наприклад, поліномами Жегалкіна є наступні логічні вирази:
f1 = X Å YZ Å XYZ
f2 = 1 Å X Å Y Å Z
