Тема 1.1 Комплексные числа. Алгебраическая форма комплексного числа.

СОДЕРЖАНИЕ

 

Пояснительная записка…………………………………………..............3

1. Тематика вопросов для самостоятельного изучения........................4

2.Задания для самостоятельной работы...................................................5-16

3. Литература……………………………………………………………..17

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.

Самостоятельная работа является одним из видов учебных занятий студентов.На самостоятельную работу в курсе изучения дисциплины отводится 32 часа.

Целью самостоятельной работы студентов является:

· систематизация и закрепление знаний и практических умений студентов;

· углубление и расширение теоретических знаний, формирование

· умений использовать дополнительную литературу;

· развитие познавательных способностей и активности студентов, творческой инициативы, самостоятельности, ответственности и организованности;

· формирование самостоятельного мышления;

· развитие исследовательских умений.

 

Выполнение самостоятельных работ является обязательным видом учебной деятельности студента. Выполнению заданий должна предшествовать подготовительная работа, а именно:

· тщательно проработать теоретический материал по записям лекций и по учебникам, разбирая при этом решенные примеры и задачи;

· осмыслить основные математические понятия, теоремы и формулы;

· разобраться в решении задач, рассмотренных на практических занятиях.

 

Оценка за самостоятельную работу выставляется в журнал учебных занятий и влияет на итоговую оценку по дисциплине.

 

Правила выполнения и оформления работ:

· Работа должна быть выполнена самостоятельно.

· Самостоятельную работу необходимо выполнить в отдельной тетради.

· На обложке тетради должны быть ясно написаны фамилия студента и номер группы.

 

ТЕМАТИКА ВОПРОСОВ ДЛЯ САМОСТОЯТЕЛЬНОГО ИЗУЧЕНИЯ

Раздел или тема	Тематика работы	Объем часов
Тема 1.1.	Комплексные числа. Алгебраическая форма комплексного числа
Тема 1.2.	Действия с комплексными числами в показательной и тригонометрической формах
Тема 2.1.	Основные понятия теории матриц
Тема 2.2.	Решение матричных уравнений.
Тема 3.1.	Производная и дифференциал
Тема 3.2.	Приложения производной
Тема 3.3.	Интегральное исчисление
Тема 3.4.	Обыкновенные дифференциальные уравнения
Тема 4.1.	Вероятность. Теорема сложения и умножения вероятностей
Тема 4.2.	Случайная величина, ее функция распределения
Тема 4.3.	Математическое ожидание и дисперсия случайной величины

Тема 1.1 Комплексные числа. Алгебраическая форма комплексного числа.

Цель: отработать навыки выполнения арифметических действий с комплексными числами.

Форма работы: решение задач.

Задания для самостоятельной работы:

1. Найти модуль и главное значение аргумента комплексных чисел:

1) ;

2) z = 3+4i;

3) z = -1+2i.

2. Выполнить сложение и вычитание комплексных чисел:

1) 2+3i и 2-3i;

2) 2+3i и -2-3i;

3) 2+3i и -2+3i.

3. Вычислить:

1) ;

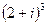2) i²⁰⁰⁴+ i¹⁹⁹⁷- i²⁵+ i¹⁶;

3) ;

4) ;

5)

 

Список рекомендуемой литературы:

1. Википедия – свободная энциклопедия http://ru.wikipedia.org/wiki

2. БогомоловН.В., СамойленкоО.Н.Математика//Учебник для техникумов.- М.:

Наука, 2004.

3. ПехлецкийИ.Д..Математика//Учебник для техникумов.- М.: Наука, 2001.

4. Щипачев В.С.. Основы высшей математики. – М.: Высшая школа, 2001.

Порядок проверки, защиты самостоятельной работы:

проверка рабочей тетради.